Algorithmen und Datenstrukturen - Algorithmen auf Zeichenreihen -
|
|
|
- Hede Fischer
- vor 6 Jahren
- Abrufe
Transkript
1 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Algorithmen und Dtenstrukturen - Algorithmen uf Zeichenreihen - Alexnder Sczyr Technische Fkultät sczyr@techfk.uni-bielefeld.de Vorlesung, Universität Bielefeld, Winter 2014/ / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Kpitel 6: Algorithmen uf Zeichenreihen Dieses Kpitel eschäftigt sich mit Algorithmen uf Zeichenreihen. Wir lernen einige wichtige und erühmte Algorithmen zur Textsuche und Textkomprimierung kennen. Als neue Progrmmiermethode tucht die Idee der Effizienzveresserung durch eine Vorverreitungsphse uf, welche die Kenntnis nur eines von zwei Argumenten vorussetzt. 2 / 74
2 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Anwendungsgeiete Anwendungsgeiete Die Verreitung von Zeichenreihen ist ein wichtiges Teilgeiet der Informtik, z.b. Erstellen, Durchsuchen, Archivieren von Dokumenten Text-Kompression & Dtenkompression (uf llen digitlen Üertrgungswegen) Genomforschung: Genome, Gene; Proteindtennken Internet-Suchmschinen 3 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Frgestellungen Frgestellungen Suchen (Muster P in Text T ) Vergleichen (Text S gegen Text T ) Clustering und Klssifizierung von Mengen von Zeichenreihen Textkomprimierung (Text T t T, worin t weniger Speicherpltz elegt ls T ). Verschlüsselung 4 / 74
3 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Frgestellungen Logische Vrinten Exkte Suche oder Vergleich (J/Nein; lle Auftreten/ein Auftreten) Approximtive Suche oder Vergleich (kleine Aweichungen erlut ester Treffer gesucht) Prweiser vs. multipler Vergleich Einfche vs. multiple Mustersuche 5 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Frgestellungen Technische Vrinten z.b. ei der Mustersuche 1 eide P und T vriel: nive Verfhren 2 P eknnt, T vriel: generiere spezielles Suchverfhren ( Mtcher ) für M in wechselnden Texten T 3 P vriel, T (reltiv) stil: generiere Index-Struktur zum schnellen Durchsuchen für wechselnde P 6 / 74
4 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Frgestellungen z.b. eim Vergleichen 4 eide Texte etw gleich groß Vergleich üer volle Länge 5 este lokle Ähnlichkeit Ws ist die ähnlichste Tonfolge in zwei Musikstücken? 6 kleiner Aschnitt in lngem Text Ws ist die dzu ähnlichste Zeichenreihe, die drin vorkommt? 7 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Frgestellungen z.b. ei großen/komprimierten Texten 7 online/streming-verfhren: Text wird nur einml gelesen, von links nch rechts 8 residente Verfhren: gnzer Text muss gleichzeitig verfügr sein für Zugriffe in elieiger Folge 8 / 74
5 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Beispiele Mehr Beispiele zu Text-Editor: Finde lle Auftreten eines Wortes; ersetze durch ein nderes 2 Üersetzung von Progrmmiersprchen: Erkennung der lexiklischen Grundsymole der Sprche in Progrmmen (Lexiklische Anlyse ls 1. Stufe der Syntxnlyse) 3 Suche nch Stichworten im Werk von Shkespere; Suche nch DNS-Muster ( ACGTAACCTTA ) im menschlichen Genom (3.3 GB) 9 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Beispiele 4 Textvergleich geschrieener (?) Husufgen; Vergleich zweier orthologer Gene (ortholog: verwndt durch Astmmung) 5 Suche nch Rukopien von Musikstücken 6 Aussortieren von Zerfllsprodukten der RNS; (sie sind Teile längerer Sequenzen; siehe uch 3) 7 Komprimieren/Dekomprimieren uf Üertrgungswegen; Verschlten von Progrmmen ls Unix pipes ; Listlessness ei funktionlen Progrmmen 8 Komplexere Suchmusternfrgen, z. B. verteilte Repets im menschlichen Genom 10 / 74
6 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Effizienz Effizienz-Betrchtung zur exkten Suche Hier eine llgemeine Vorusetrchtung zur Effizienz noch hen wir keine Algorithmen gesehen. Sei die Länge des Musters P: P = m, und die Länge des Textes T: T = n. Ws wäre die worst-cse Effizienz einer exkten Suche? Untergrenze der worst-cse Effizienz: O(m + n), denn lle Zeichen im Muster/Text müssen mindestens einml gelesen werden. O(m n) ist trivil erreichr ei Vorverreitung von Muster oder Text muss der Generierungsufwnd gegen veresserten Suchufwnd gewogen werden (mortisierte Effizienz) 11 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Effizienz Die solute Untergrenze für ds Finden von P nch Vorverreitung von T ist O(m) ds wäre unhängig von der Größe des Textes! Eine Besonderheit wird wichtig ei sehr großen Texten: Größe des Index knn kritisch werden. Ds Loklitätsverhlten der Indexkonstruktion und der Suche spielt eine Rolle in Rechnern mit Cche-Architektur (Thrshing) 12 / 74
7 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Effizienz Konstnte Fktoren Der Vergleich zweier Zeichen ist chrkteristische Opertion Ansonsten wird kum etws gerechnet Konstnte Fktoren sind generell gering, symptotische Lufzeit ist hrtes Kriterium Ausnhme: Thrshing-Phänomene 13 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Grundlegende Definitionen Die Suche nch llen (exkten) Vorkommen eines Musters in einem Text ist ein Prolem, ds häufig uftritt (z.b. in Editoren, Dtennken etc.). Wir vereinren folgende Konventionen: Alphet Σ endlicher Zeichenvorrt Muster P = P[0..m 1] Σ m Text T = T [0..n 1] Σ n P[j] = Zeichen n der Position j P[..e] = Teilwort von P von is den Positionen und e Beispiel P = cde, P[0] =, P[3] = d, P[2..4] = cde. 14 / 74
8 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Nottion leeres Wort: ɛ Länge eines Wortes x: x Konktention zweier Wörter x und y: xy 15 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Präfix und Suffix Sei x = uvw, mit u, v, w. Dnn heißt u Präfix von x, v Teilwort von x und w Suffix von x. Bechte: c ht Präfixe ɛ,,, c und die Suffixe c, c, c, ɛ. 16 / 74
9 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Ds Prolem der exkten Suche Definition Ein Muster P kommt mit der Verschieung s im Text T vor, flls 0 s n m und T [s..(s + m 1)] = P[0..(m 1)] gilt. In diesem Fll nennen wir s eine gültige Verschieung. Ds Prolem der exkten Textsuche ist es, lle gültigen Verschieungen zu finden. Mn knn er z.b. uch sgen: Finde lle Suffixe von T, die P ls Präfix hen. Beispiel T = ielefeld oh ielefeld P = feld s = 5 und s = 18. Gültige Verschieungen: 17 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Wir entwickeln eine nive Lösung. Die nive Lösung des Prolems sieht so us: nive1 p t = [i i <- [0..length t - 1], p == tke (length p) (drop i t)] Diese Lösung ist offensichtlich NICHT effizient sie führt zum Aufwnd O(n 2 + 2nm) wegen der Aufrufe von drop. 18 / 74
10 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Besser ist die Vrinte nive2 p t = [i (i,w) <- zip [0..] (suffixes t), p == tke m w] where m = length p suffixes [] = [[]] suffixes (x:xs) = (x:xs) : suffixes xs Hier ist der worst-cse Aufwnd O(m n) 19 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Am Beispiel T = rkdrxs und P = rxs erkennt mn ds ineffiziente Vorgehen, insesondere wenn Text und Muster immer komplett verglichen werden: r k d r x s r x s r x s r x s r x s r x s r x s r x s r x s r x s 20 / 74
11 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Selst wenn Text und Muster zeichenweise von links nch rechts und nur is zum ersten Mismtch 1 verglichen werden, ist die worst-cse Zeiteffizienz des niven Algorithmus O ( n m ), z.b. wird für T = n, P = m der Vergleich p =... n m + 1 ml usgeführt und in jedem Test in werden m Zeichen verglichen. Wie knn mn den niven Algorithmus veressern? Idee 1: Üerspringe ein Teilwort w von T, flls klr ist, dss w P (BM-Algorithmus 1977). Idee 2: Merke Informtionen üer isherige Vergleiche und nutze diese, um neue, unnötige Vergleiche zu vermeiden (KMP-Algorithmus 1977). 1 Die zwei Zeichen stimmen nicht üerein. 21 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Der Boyer-Moore-Algorithmus Der BM-Algorithmus legt wie der nive Algorithmus ds Muster zunächst linksündig n den Text, vergleicht die Zeichen des Musters dnn er von rechts nch links mit den entsprechenden Zeichen des Textes. Beim ersten Mismtch enutzt er zwei Lufzeit-Heuristiken, um eine Verschieung des Musters nch rechts zu estimmen. Beispiel: T = RHABARBERBARBARA P = BARBIER 22 / 74
12 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Ergenis-Heuristik Eine Ergenis-Heuristik (uch mnchml nur ls Heuristik ezeichnet) findet ein gutes, er nicht unedingt optimles Ergenis. Lufzeit-Heuristik Eine Lufzeit-Heuristik findet immer ein korrektes Ergenis und versucht durch Akürzungen möglichst die Lufzeit zu drücken. 23 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Die d-chrcter Heuristik Flls eim Vergleich von P[0..m 1] und T [s..s + m 1] (von rechts nch links) ein Mismtch P[j] T [s + j] für ein j mit m 1 j 0 festgestellt wird, so schlägt die d-chrcter Heuristik BCH(T [s + j]) eine Verschieung des Musters um j k Positionen vor. Dei ist k der größte Index (0 k m 1) mit T [s + j] = P[k]. Wenn kein k mit T [s + j] = P[k] existiert, so sei k = 1. BCH knn ereits vor Beginn der Suche erechnet werden!! 24 / 74
13 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Gerucht wird: [ ] BCH T [s + j] [ ] BCH T [s + j] = 1, flls T [s + j] nicht in P { } = mx k P[k] = T [s + j] 0 k m 1 Berechnet wird im Vorus: BCH[] = mx 0 k m 1 { } k P[k] = [ ] Flls BCH T [s + j] = 1, so knn ds Muster um j 1 verschoen werden (siehe vorherige Folie). 25 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Einfcher gesgt: T [s + j] ist der d chrcter. Wir verschieen ds Muster so, dss ds Auftreten des d chrcter im Muster m weitesten rechts, lso P[k], unter T [s + j] liegt. Prolem: Wenn k > j, würde ds Muster nch links verschoen! Dher wird eine weitere Heuristik enötigt. 26 / 74
14 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Die good-suffix Heuristik Flls eim Vergleich von P[0..m 1] und T [s..s + m 1] (von rechts nch links) ein Mismtch P[j] T [s + j] für ein j mit m 1 j 0 festgestellt wird, so wird ds Muster so weit nch rechts geschoen, is ds eknnte Suffix T [s + j + 1..s + m 1] wieder uf ein Teilwort des Musters psst. 27 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Genuer: Flls ein Suffix von P mtcht, er ds nächste Zeichen links im Text nicht mtcht, dnn suche die m weitesten rechts stehende Stelle in P, n der ds mtchende Suffix uftritt, er ei dem ds nächste Zeichen links in P ein nderes ist (sonst würde es wieder nicht pssen). P knn dnn soweit nch rechts verschoen werden, dss die neue Stelle unter der lten zu liegen kommt. Flls ds mtchende Suffix nicht noch ml in P zu finden ist, dnn verschiee die linke Position von P üer die zuletzt etrchtete Position im Text hinus, so dss ein Prefix von P noch ds Suffix von P mtcht. Flls ds nicht zutrifft, dnn knn um die gnze Länge des Ptterns verschoen werden. Flls P gefunden wird, dnn knn dnch soweit verschoen werden, wie ds größte echte Prefix von P, ds mit einem Suffix von P üereinstimmt. Ansonsten knn um die Länge von P verschoen werden. 28 / 74
15 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Zusmmenspiel der Heuristiken Im Boyer-Moore-Algorithmus wird ds Muster um ds Mximum von eiden vorgeschlgenen Verschieungen verschoen. Es knn gezeigt werden, dss die Lufzeitkomplexität dnn im worst cse O(n + m) ist. 29 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Vorverreitung: Bd chrcter Heuristik: Good suffix Heuristik: Zusmmen Die Verschieespnnen eider Heuristiken werden vor durch Anlyse von P ermittelt und telliert BCH: [ 1..m 1] BCH() = k gdw. k ist rechtestes Auftreten von in P; oder BCH() = 1 GSH: [0..m 1] [ 1..m 1] GSH(j) = min(gsh (j), GSH (j)) GSH (j) = j + 1 mx r : P[r..r + (m 1) (j + 1)] = P[j + 1..m 1] sonst m GSH (j) = (m 1) mx q < ((m 1) j) : P[0..q] = P[(m 1) q..(m 1)] s = s + mx(j BCH(T [s + j]), GSH(j)) 30 / 74
16 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Beispiel Die d-chrcter Heuristik schlägt eine Verschieung von j k = (m 3) 5 = (12 3) 5 = 4 Positionen vor; dies ist im Fll () illustriert. Aus der Drstellung (c) wird ersichtlich, dss die good-suffix Heuristik eine Verschieung von 3 Positionen vorschlägt. Also wird ds Muster um mx{4, 3} = 4 Positionen nch rechts verschoen. d chrcter good suffix {}} {... w r i t t e n n o t i c e t h t... s r e m i n i s c e n c e ()... w r i t t e n n o t i c e t h t... s + 4 r e m i n i s c e n c e ()... w r i t t e n n o t i c e t h t... s + 3 r e m i n i s c e n c e (c) 31 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Ein Beispiel, in dem die Bd-Chrcter-Heuristik eine Verschieung nch links (negtiv) vorschlägt:... R H A B A R B E R B A R B A R A B R A... B I E R B A R rechtes Auftreten von t in P d chrcter t ergit Verschieung 3! Good suffix Heuristik: Verschieung / 74
17 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Wirksmkeit der Heuristiken: lnge gute Suffixe sind selten, in der Regel eruhen große Verschieungen uf der d-chrcter Heuristik 33 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Der Boyer-Moore-Horspool-Algorithmus Der BM-Algorithmus verdnkt seine Schnelligkeit vor llem der d-chrcter Heuristik. Dher wurde 1980 von Horspool eine Vereinfchung des BM-Algorithmus vorgeschlgen: Die d-chrcter Heuristik wird derrt modifiziert, dss sie immer eine positive Verschieung vorschlägt. Dmit wird die good-suffix Heuristik üerflüssig (und uch die Vorverreitung einfcher). 34 / 74
18 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Der Boyer-Moore-Horspool-Algorithmus Der BMH-Algorithmus geht in den meisten Fällen nlog zur isherigen d-chrcter Heuristik vor. Aer: Flls P[j] T [s + j] für ein j (0 j m 1) gilt, so wird s um m 1 k erhöht, woei k der größte Index zwischen 0 und m 2 ist mit T [s + m 1] = P[k]. Wenn kein k (0 k m 2) mit T [s + m 1] = P[k] existiert, so wird s um m erhöht. Ds Muster wird lso um ( ) λ T [s + m 1] = min ( {m} { m 1 k 0 k m 2, T [s + m 1] = P[k] verschoen. ( Wenn) ein Mtch gefunden wurde, dnn wird eenflls um λ T [s + m 1] verschoen. Vorverreitung: λ(c) für lle c Σ. }) 35 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Verhlten des BMH-Algorithmus ei einem Mismtch... g o l d e n f l e e c e o f... s r e m i n i s c e n c e... g o l d e n f l e e c e o f... s + 3 r e m i n i s c e n c e 36 / 74
19 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Verhlten des BMH-Algorithmus ei einem Treffer... g o l d e n f l e e c e o f... s f l e e c e... g o l d e n f l e e c e o f... s + 2 f l e e c e 37 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Boyer-Moore-Horspool Algorithmus in Hskell import Arry Eine hlherzige Lösung lmd :: String -> String -> Int -> Int lmd p t s = minimum (m:[m-1-k k <- [0..(m-2)], t!!(s+m-1) == p!!k]) where m = length p Mh :: String -> String -> [Int] Mh p t = mh 0 p t where mh i p t i > (length t)-(length p) = [] p == (tke (length p) (drop i t)) = i:(mh (i + lmd p t i) p t) otherwise = mh (i + lmd p t i) p t 38 / 74
20 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Kritik: 1 Die Repräsenttion von Muster und Text ls String sttt ls Arry verhindert ds Erreichen guter Effizienz. 2 Die Verschieefunktion λ wird nicht vor erechnet, sondern ei jedem Geruch neu. 3 Für die lokle Funktion mh sind p und t eknnt. Es ist unnötig, sie jedesml ls (unveränderte) Prmeter zu üergeen. 4 λ sollte lokle Funktion von mh sein, d uch dfür p und t konstnt sind. 5 Eine zentrle BMH-Idee ist, dss λ() für lle us [ A.. z ] erechnet wird. Ddurch wird λ unhängig von Text t!! 39 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Eine korrekte Lösung type SArr = Arry Int Chr mh:: SArr -> SArr -> [Int] mh p t = mhi 0 m where (_,m) = ounds p (_,n) = ounds t mhi i k i+m >n = [] k == 0 = [i t!i == p!0]++ mhi (i+shift!(t!(i+m))) m t!(i+k) == p!k = mhi i (k-1) otherwise = mhi (i+shift!(t!(i+m))) m shift :: Arry Chr Int shift = ccumarry min (m+1) ( A, z ) [(p!k,m-k) k <- [0..m-1]] 40 / 74
21 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Zum Aufruf mit zwei Strings tmh p t = mh (mk p) (mk t) where mk s = listarry (0,length s -1) s Zum seprt Angucken eine ent-loklisierte Kopie von shift shift :: SArr -> Arry Chr Int shift p = ccumarry min (m+1) ( A, z ) [(p!k,m-k) k <- [0..m-1]] where (_,m) = ounds p 41 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Der Knuth-Morris-Prtt-Algorithmus Der nive Algorithmus: r k d e r r k d r k r k d r r k d r r k d r r k d r r k d r etc. 42 / 74
22 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Ws zeigt uns eine genuere Anlyse des Vorgehens? Im zweiten und dritten Schritt wird ds Zeichen n Position 1 im Muster mit den Zeichen und r n der zweiten und dritten Position des Textes verglichen wird, owohl ereits nch dem positiven Vergleich von r klr sein musste, dss hier keine Üereinstimmung existieren knn. 43 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Der Knuth-Morris-Prtt-Algorithmus geht nch folgendem Schem vor: Wenn ein Teilwort (Präfix) des Musters ereits erknnt wurde, er dnn ein Mismtch uftritt, so ermittelt der Algorithmus ds längste Präfix dieses Teilwortes, ds gleichzeitig echtes Suffix dvon ist, und schiet ds Muster dnn so weit nch rechts, dss dieses Präfix n der isherigen Position des Suffixes liegt. r k d e r r k d r k r k d r r k d r r k d r r k d r r k d r r k d r r k d r r k d r Mn erkennt, dss hier nch dem Verschieen 2 zw. 4 zw. 1 unnötige Vergleiche vermieden wurden. 44 / 74
23 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Beispiel: Die Präfixfunktion π : {1, 2,..., m} {0, 1,..., m 1} für ein Muster P[0..m 1] ist definiert durch π[q] = mx{k : k < q und P[0..k 1] ist echtes Suffix von P[0..q 1]}. Sie lutet für unser Beispielwort P = rkdr: q P[q] r k d r π[q] Für q = 9 wäre ds entsprechende Teilmuster lso rkd. Ds längste Präfix, ds gleichzeitig echtes Suffix dvon ist, ist. Es ht die Länge 2, drum findet sich in der Telle n der Position q = 9 der Eintrg π[q] = 2. P wird so verschoen, dss P[π(q)] unter der Mismtch-Position in T steht, d. h. S S + q π[q]. 45 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Berechnung der Präfixfunktion für KMP Vorgehen: induktiv Annhme: Die Werte von π sind ereits für 1... q 1 erechnet. Gesucht: π[q] = mx{k k < q und P[0..k 1] ist echtes Suffix von P[0..q 1]}. Welche k kommen in Frge? lle echten Suffixe von P[0..q 2], die sich zu einem echten Suffix von P[0..q 1] erweitern lssen. 46 / 74
24 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression () 0 k 2 k q 2 q 1 x x k 1 k 1 Sei k 1 = π[q 1] + 1 Dnn ist π[q] = k 1 flls, P[k 1 1] = P[q 1]. 47 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression () ndernflls (y x): k 2 1 k 1 1 q 2 q 1 x y x k 2 k 2 k 2 Sei k 2 = π[k 1 1] + 1. Dnn ist π[q] = k 2, flls P[k 2 1] = P[q 1] und so weiter / 74
25 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Allgemein: k i = π[k i 1 1] + 1 = π[π[k i 2 1] + 1 1] + 1 = π[π[k i 2 1]] + 1 k i = π i [q 1] / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression KMP-Algorithmus in Hskell import Arry Eine hlherzige Lösung für KMP (einschließlich einer esonders peinlichen Implementierung von suffixes) Pi-Funktion für den KMP: pi :: String -> Arry Int Int pi p = rry (1,qmx) [ (q, mximum [ k k <- [0..q], (tke k p) elem (suffixes (tke q p)) ]) q <- [1..qmx] ] where qmx = (length p) 50 / 74
26 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Git lle echten Suffixe eines Worts inklusive des leeren Worts us: suffixes :: [] -> [[]] suffixes s = [ (drop n s) n <- [1..(length s)] ] Git die Stelle des ersten unterschiedlichen Zeichens in zwei gleich lngen Strings us: getq :: String -> String -> Int getq = getq 0 where getq i (:s) (:s) = if /= then i else getq (i+1) s s getq i [] [] = i 51 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Führt den KMP us: kmp :: String -> String -> [Int] kmp [] _ = error "ungueltiger Suchstring" kmp p t = kmp 0 p t where kmp i p t i > lt-m = [] q == m && k == 0 = i:kmp (i + m) p t q == m && k > 0 = i:kmp (i + m - k ) p t q < m && p!!q /= t!!(i+q) && q /= 0 = kmp (i + q - pq) p t q < m && p!!q /= t!!(i+q) && q == 0 = kmp (i+1) p t where q = getq p (tke m (drop i t)) k = pit!m pq = pit!q pit = pi p lt = length t m = length p 52 / 74
27 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Kritik: 1 Drstellung von Text und Muster ls String (sttt Arry) torpediert die Effizienz. 2 Suffixes hen wir in den Üungen schon elegnter implementiert diese Implementierung ist in O(n 2 )! 3 getq vergleicht im Muster jedesml von gnz vorne, ds stimmt nicht mit der KMP-Idee üerein. 4 kmp ls lokle Funktion von KMP rucht keine Prmeter p und t. 53 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Eine korrekte Implementierung von KMP type SArr = Arry Int Chr kmp p t = kmp 0 0 where (_,m) = ounds p (_,n) = ounds t kmp i q i+m > n = [] q == m+1 = i:kmp (i+q-pi!q) (pi!q) - i+q leit invrint! t!(i+q) == p!q = kmp i (q+1) - q rueckt vor q == 0 = kmp (i+1) 0 - i rueckt vor otherwise = kmp (i+q-pi!q) (pi!q) - i+q leit invrint! pi :: Arry Int Int pi = rry (0,m+1) ((0,0):(1,0):[(q,itertep (pi!(q-1)) q) q <- [2..m+1]]) where itertep 0 q = if p!0 == p!(q-1) then 1 else 0 itertep k q = if p!k == p!(q-1) then k+1 else itertep (pi!k) q 54 / 74
28 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Zum Aufruf von kmp mit zwei Strings tkmp p t = kmp (mk p) (mk t) where mk s = listarry (0,length s -1) s Ent-loklisierte Version von pi zum Reingucken pt p = pi where (_,m) = ounds p pi = rry (0,m+1) ((0,0):(1,0):[(q,itertep (pi!(q-1)) q) q <- [2..m+1]]) itertep 0 q = if p!0 == p!(q-1) then 1 else 0 itertep k q = if p!k == p!(q-1) then k+1 else itertep (pi!k) q mk s = listarry (0,length s -1) s 55 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Ein Wettrennen zwischen KMP und BMH 1. Stz: p = ccggt, t = tcgtggctgctgtgtttgcgccggcgttgctgcccgtccggtcxggct tkmp p t [53] (11975 reductions, cells) tmh p t [53] (7473 reductions, 9958 cells) 0:1 2. Stz: p =, t = tkmp p t [0,28] (10881 reductions, cells) tmh p t [0,28] (12374 reductions, cells) 1:0 3. Stz: p = WerdurchTesten, t = Progrmmeverstehenwilldermussschonsehrvielmessenundgnzgenuhinsehen tkmp p t [] (8068 reductions, cells) tmh p t [] (5979 reductions, 8064 cells) 0:1 Ergenis:... KMP : BMH 1: / 74
29 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Weitere Verfhren Auch eim KMP-Algorithmus wird ein Textuchste ei Mismtch mehrfch verglichen. Ein endlicher Automt dgegen mcht pro Üergng genu einen Vergleich! Ein Zwischenschritt uf dem Weg dorthin ist der Aho-Corsick-Automt. 57 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Aho-Corsick-Automt Bei mehr ls einem Muster ilden lle Präfixe ller Muster die Zustndsmenge des Aho-Corsick-Automten. Beispiel: P 1 = r, P 2 =, P 3 = rr. =, ε r r r r r r r r rr rr 58 / 74
30 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Aho-Corsick-Automt (2) Der Aho-Corsick-Automt knn nch mehreren Mustern gleichzeitig suchen. Die gestrichelten Üergänge gelten für den Mismtch. Nch einem Mismtch-Üergng wird ds gleiche Zeichen wieder gelesen. So können Ketten von Mismtch-Üergängen entstehen, ohne dss der Automt im Text fortschreitet. 59 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression KMP-Algorithmus ls AC-Automt mit Mismtch-Üergängen (ohne Kntenmrkierung; ohne Weitergehen im Text) Jeder Zustnd entspricht einem erknnten Präfix; die Nummer ist q us der π-telle = ε r r 3 r k rk 4 5 rk 6 d rkd 7 rkdr 11 rkdr 10 r rkd 9 rkd 8 Speicherpltz für den KMP-Automt: O( P ) für die Telle der Spontnüergänge. 60 / 74
31 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Vermeiden von Mismtch-Üergängen Bei einem Mismtch-Üergng ist der d chrcter im Text eknnt. Sei x dieser Buchste. Ds Üergngsdigrmm legt ereits fest, nch wie vielen Mismtch-Üergängen ein regulärer Üergng unter x möglich wird. Ein endlicher Automt mcht diesen Üergng direkt rucht er eine größere Üergngstelle. 61 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Trnsformtion des KMP-Automten in einen endlichen Automten (Zusmmenziehen der spontnten Üergänge, so dss ei jedem Üergng ein Zeichen gelesen wird) = ε 0 =,,k =, 1 =,r = 2 rkdr 11 k r r 3 rkdr 10 =,,k = r r k rk 4 5 rkd 9 rkd 8 rk 6 rkd 7 d =,,d = = =,r =, Speicherpltz für endlichen Automt: O( P ) für lle Komintionen von Zeichen und Zustnd. 62 / 74
32 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Index-sierte Verfhren Sehr große Texte, die sich selten ändern, können zu einem Index verreitet werden, in dem in O(m) oder O(m log n) gesucht werden knn suffix rry: O(m log n) suffix tree: O(m) enhnced suffix rry: O(m) Alle Indices ruchen O(n) Speicherpltz und können in O(n) Zeit konstruiert werden. Vorlesung Sequenznlyse 63 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Textkompression Verfhren zur Textkompression sind llgegenwärtig in Dtenüertrgung und Archivierung. Dei sollte mn nicht nur n sprchliche Texte denken, sondern uch Bilder und Messdten. Wir etrchten 2 Vrinten des Lempel-Ziv-Verfhrens. 64 / 74
33 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Grundidee: Sustitutionsverfhren A B A B B A komprimiert den Text mit der Sustitutionstlle A: B: Reduktion: 21 Zeichen Zeichen Proleme: Aufwnd zur Konstruktion der Telle Pltzedrf für die Telle Whl der Telle (nicht eindeutig) 65 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Grundidee Lempel-Ziv Die Telle wird on-the-fly ei der Kompression konstruiert Sie wird NICHT gespeichert, sondern sie wird ei der Dekompression rekonstruiert. 66 / 74
34 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Lempel-Ziv 1978 Die Telle enthält nummerierte Phrsen, initil nur (0, ) Der Text wird links rechts gelesen, und von der jeweils ktuellen Position us wird ds längste Teilwort w estimmt, ds ereits ls Phrse die Nummer sei i in der Telle steht, sowie der Folgeuchste x im Text die Codierung (i, x) usgegeen die neue Phrse (j, wx) eingetrgen 67 / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Beispiel Lempel-Ziv 1978 Kompression Einge: 0 : ε Je länger die Phrsen werden und je mehr sie sich wiederholen, desto stärker wird die Kompression. 68 / 74
35 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Beispiel Lempel-Ziv 1978 Dekompression Wir kennen nur ds Alphet {, } und den komprimierten Text C= Wir rekonstruieren gleichzeitig Text und Telle : ε / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Lempel-Ziv-Welch 1984 Eine Vereinfchung ergit sich, wenn mn nnimmt, dss lle Einzeluchsten ls Phrsen vorkommen: die Telle wird sttt mit (0, ) mit (i, i ) initilisiert für = (1,..., ) n jeder Position wird mit i, w, x wie zuvor die Phrsennummer i usgegeen ohne Buchste! die neue Phrse wx eingetrgen die Rekonstruktion der Telle enötigt nun etws Vorusschu. 70 / 74
36 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Lempel-Ziv-Welch 1984 Kompression / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression Lempel-Ziv-Welch 1984 Dekompression Im Schritt für 1 wird Phrse 3 eingetrgen. Dei wird 2 mitenutzt für den neuen Buchsten. Im Schritt für 3 wird Phrse 9 eingetrgen. Dei wird 9 mitenutzt für den neuen Buchsten! 72 / 74
37 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression 2. Beispiel LZW84 Kompression Zum Selermchen / 74 Algorithmen uf Zeichenreihen Grundlegende Definitionen BM-Algorithmus BMH-Algorithmus Der KMP-Algorithmus Weitere Verfhren Textkompression 2. Beispiel LZW84 Dekompression Zum Selermchen / 74
dem Verfahren aus dem Beweis zu Satz 2.20 erhalten wir zunächst die folgenden beiden ε-ndeas für die Sprachen {a} {b} und {ε} {a} +
 Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Deterministische endliche Automaten
 Endliche Automten Idee: endlicher Automt A ht endlich viele innere Zustände liest Einge wєσ* zeichenweise von links nch rechts git zum Schluß eine J/Nein Antwort A Lesekopf w 1 w 2 w n gelesenes Symol
Endliche Automten Idee: endlicher Automt A ht endlich viele innere Zustände liest Einge wєσ* zeichenweise von links nch rechts git zum Schluß eine J/Nein Antwort A Lesekopf w 1 w 2 w n gelesenes Symol
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
 Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN
 Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Franz Binder. Vorlesung im 2006W
 Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
Formle Reguläre und Formle Institut für Alger Johnnes Kepler Universität Linz Vorlesung im 2006W http://www.lger.uni-linz.c.t/students/win/ml Formle Inhlt Reguläre Reguläre Formle Zustndsdigrmm δ: Σ (Q
1.7 Inneres Produkt (Skalarprodukt)
 Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
Grundbegriffe der Informatik
 Grundegriffe der Informtik Einheit 14: Endliche Automten Thoms Worsch Krlsruher Institut für Technologie, Fkultät für Informtik Wintersemester 2009/2010 1/56 Üerlick Erstes Beispiel: ein Getränkeutomt
Grundegriffe der Informtik Einheit 14: Endliche Automten Thoms Worsch Krlsruher Institut für Technologie, Fkultät für Informtik Wintersemester 2009/2010 1/56 Üerlick Erstes Beispiel: ein Getränkeutomt
vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimalautomat: minimaler vollständiger DFA
 Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
Ws isher geschh NFA A = (X, Q, δ, I, F ) vollständig (Vervollständigung) deterministisch, DFA (Potenzmengenkonstruktion) Minimlutomt: minimler vollständiger DFA Für jede Sprche L X sind die folgenden Aussgen
DEA1 Deterministische Version
 Endliche Automten 4 Deterministische endliche Automten Zu dem nichtdeterministischen Automten EA git es eine deterministische Version. EA Akzeptor für Wörter üer X = { } mit mindestens einem führenden.
Endliche Automten 4 Deterministische endliche Automten Zu dem nichtdeterministischen Automten EA git es eine deterministische Version. EA Akzeptor für Wörter üer X = { } mit mindestens einem führenden.
ARBEITSBLATT 5L-6 FLÄCHENBERECHNUNG MITTELS INTEGRALRECHNUNG
 Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Definition Suffixbaum
 Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
10 Anwendungen der Integralrechnung
 9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
Theoretische Informatik und Logik Übungsblatt 2 (2013S) Lösung
 Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
1 Folgen von Funktionen
 Folgen von Funktionen Wir etrchten Folgen von reell-wertigen Funktionen f n U R mit Definitionsereicht U R und interessieren uns für ntürliche Konvergenzegriffe. Genuer setzen wir uns mit folgenden Frgen
Folgen von Funktionen Wir etrchten Folgen von reell-wertigen Funktionen f n U R mit Definitionsereicht U R und interessieren uns für ntürliche Konvergenzegriffe. Genuer setzen wir uns mit folgenden Frgen
Endliche Automaten 7. Endliche Automaten
 Endliche Automten 7 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte
Endliche Automten 7 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte
Nullstellen quadratischer Gleichungen
 Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
MC-Serie 12 - Integrationstechniken
 Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
Anlysis D-BAUG Dr. Meike Akveld HS 15 MC-Serie 1 - Integrtionstechniken 1. Die Formel f(x) dx = xf(x) xf (x) dx i) ist im Allgemeinen flsch. ii) folgt us der Sustitutionsregel. iii) folgt us dem Huptstz
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Wirtschaftsmathematik 00053: Mathematik für Wirtschaftswissenschaftler I Kurseinheit 2: Lineare Algebra II. Autor: Univ.-Prof. Dr.
 Wirtschftsmthemtik 0005: Mthemtik für Wirtschftswissenschftler I Kurseinheit : Linere Alger II Leseproe Autor: Univ.-Prof. Dr. Wilhelm Rödder 5. Linere Gleichungssysteme und Mtrixgleichungen So verwundert
Wirtschftsmthemtik 0005: Mthemtik für Wirtschftswissenschftler I Kurseinheit : Linere Alger II Leseproe Autor: Univ.-Prof. Dr. Wilhelm Rödder 5. Linere Gleichungssysteme und Mtrixgleichungen So verwundert
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
Berechnung von Flächen unter Kurven
 Berechnung von Flächen unter Kurven Es soll die Fläche unter einer elieigen (stetigen) Kurve erechnet werden. Dzu etrchten wir die (sog.) Flächenfunktion, mit der die zu erechnende Fläche qusi ngenähert
Berechnung von Flächen unter Kurven Es soll die Fläche unter einer elieigen (stetigen) Kurve erechnet werden. Dzu etrchten wir die (sog.) Flächenfunktion, mit der die zu erechnende Fläche qusi ngenähert
Die Keplersche Fassregel
 Die Keplersche Fssregel K. Gerer Bei vielen Aufgen, z.b. ei der Lösung von Differentilgleichungen, tucht die Schwierigkeit uf, dss Integrtionen nicht durchgeführt werden können. So können z.b. die folgenden
Die Keplersche Fssregel K. Gerer Bei vielen Aufgen, z.b. ei der Lösung von Differentilgleichungen, tucht die Schwierigkeit uf, dss Integrtionen nicht durchgeführt werden können. So können z.b. die folgenden
Klausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2013)
 Berlin, 17.07.2013 Nme:... Mtr.-Nr.:... Klusur TheGI 2 Automten und Komplexität (Niedermeier/Hrtung/Nichterlein, Sommersemester 2013) 1 2 3 4 5 6 7 8 Σ Bereitungszeit: mx. Punktezhl: 60 min. 60 Punkte
Berlin, 17.07.2013 Nme:... Mtr.-Nr.:... Klusur TheGI 2 Automten und Komplexität (Niedermeier/Hrtung/Nichterlein, Sommersemester 2013) 1 2 3 4 5 6 7 8 Σ Bereitungszeit: mx. Punktezhl: 60 min. 60 Punkte
2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004
 Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
7 Modellierung von Abläufen 7.1 Endliche Automaten
 7 Modellierung von Aläufen 7. Endliche Automten Mod-7. Endlicher Automt: Formler Klkül zur Spezifiktion von relen oder strkten Mschinen. Sie regieren uf äußere Ereignisse, ändern ihren inneren Zustnd,
7 Modellierung von Aläufen 7. Endliche Automten Mod-7. Endlicher Automt: Formler Klkül zur Spezifiktion von relen oder strkten Mschinen. Sie regieren uf äußere Ereignisse, ändern ihren inneren Zustnd,
Ungleichungen. Jan Pöschko. 28. Mai Einführung
 Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Grundkurs Mathematik. Einführung in die Integralrechnung. Lösungen und Ergebnisse zu den Aufgaben
 Seite Einführung in die Integrlrechnung Lösungen und Ergenisse Gr Stefn Gärtner Grundkurs Mthemtik Einführung in die Integrlrechnung Lösungen und Ergenisse zu den Aufgen Von llen Wissenschftlern können
Seite Einführung in die Integrlrechnung Lösungen und Ergenisse Gr Stefn Gärtner Grundkurs Mthemtik Einführung in die Integrlrechnung Lösungen und Ergenisse zu den Aufgen Von llen Wissenschftlern können
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
11. DER HAUPTSATZ DER DIFFERENTIAL- UND INTEGRALRECHNUNG
 91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
91 Dieses Skript ist ein Auszug mit Lücken us Einführung in die mthemtische Behndlung der Nturwissenschften I von Hns Heiner Storrer, Birkhäuser Skripten. Als StudentIn sollten Sie ds Buch uch kufen und
Grenzwerte von Funktionen
 Grenzwert und Stetigkeit von Funktionen Methodische Bemerkungen H Hinweise und didktisch-methodische Anmerkungen zum Einstz der Areitslätter und Folien für den Themenkreis Grenzwert und Stetigkeit von
Grenzwert und Stetigkeit von Funktionen Methodische Bemerkungen H Hinweise und didktisch-methodische Anmerkungen zum Einstz der Areitslätter und Folien für den Themenkreis Grenzwert und Stetigkeit von
1. Formale Sprachen Formale Sprachen
 1. Formle Sprchen Formle Sprchen 1. Formle Sprchen 1.1. Ws ist eine formle Sprche? Wenn mn einen Gednken in einer ntürlichen Sprche usdrücken will, kommt es im wesentlichen uf 2 Aspekte n: 1. Der korrekte
1. Formle Sprchen Formle Sprchen 1. Formle Sprchen 1.1. Ws ist eine formle Sprche? Wenn mn einen Gednken in einer ntürlichen Sprche usdrücken will, kommt es im wesentlichen uf 2 Aspekte n: 1. Der korrekte
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Spiele und logische Komplexitätsklassen
 Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Multiplikative Inverse
 Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
v P Vektorrechnung k 1
 Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
1 Grundlagen der Theorie formaler Sprachen
 1 Grundlgen der Theorie formler Sprchen Wir eginnen dmit, dss wir in diesem Kpitel zunchst einige grundlegende Begriffe und Methoden us der Theorie formler Sprchen, insesondere der regulären Sprchen, wiederholen.
1 Grundlgen der Theorie formler Sprchen Wir eginnen dmit, dss wir in diesem Kpitel zunchst einige grundlegende Begriffe und Methoden us der Theorie formler Sprchen, insesondere der regulären Sprchen, wiederholen.
Endliche Automaten. S. Kuske: Endliche Automaten; 6.Novenber 2006
 1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
5.5. Integralrechnung
 .. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
.. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
Wann wird der relative Fehler groß?
 Wnn wird der reltive Fehler groß? Wenn >> c, oder c 0 Andere Reihenfolge der Berechnung liefert Fktoren (c)/(c) oder (c)/(c) ; Es wird jeweils der Fehler, der ei der ersten Addition uftritt, verstärkt.
Wnn wird der reltive Fehler groß? Wenn >> c, oder c 0 Andere Reihenfolge der Berechnung liefert Fktoren (c)/(c) oder (c)/(c) ; Es wird jeweils der Fehler, der ei der ersten Addition uftritt, verstärkt.
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Endliche Automaten. Stoyan Mutafchiev. Programming Systems Lab, Universität des Saarlandes, Saarbrücken
 Endliche Automten Stoyn Mutfchiev Progrmming Systems L, Universität des Srlndes, Srrücken Astrct Gegenstnd dieser Areit ist der endliche Automt, sowie die Aschlusseigenschften der Sprchen, die von endlichen
Endliche Automten Stoyn Mutfchiev Progrmming Systems L, Universität des Srlndes, Srrücken Astrct Gegenstnd dieser Areit ist der endliche Automt, sowie die Aschlusseigenschften der Sprchen, die von endlichen
c dl SPiC (Teil C, SS 11) 13 Zeiger und Felder 13.1 Zeiger Einführung 13 1 Zeigervariable := Behälter für Verweise ( Adresse) Beispiel int x = 5;
 Überblick: Teil C Systemnhe Softwreentwicklung Einordnung: Zeiger (Pointer) Literl: Drstellung eines Wertes 0110 0001 12 Progrmmstruktur und Module Vrible: Bezeichnung chr ; eines Dtenobjekts Behälter
Überblick: Teil C Systemnhe Softwreentwicklung Einordnung: Zeiger (Pointer) Literl: Drstellung eines Wertes 0110 0001 12 Progrmmstruktur und Module Vrible: Bezeichnung chr ; eines Dtenobjekts Behälter
Kapitel IV Euklidische Vektorräume. γ b
 Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Teil V: Formale Sprachen
 Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Grundbegriffe der Informatik Aufgabenblatt 5
 Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
Grundegriffe der Informtik Aufgenltt 5 Mtr.nr.: Nchnme: Vornme: Tutorium: Nr. Nme des Tutors: Ausge: 20. Novemer 2013 Age: 29. Novemer 2013, 12:30 Uhr im GBI-Briefksten im Untergeschoss von Geäude 50.34
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
ARBEITSBLATT 14 ARBEITSBLATT 14
 Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Public-Key-Verfahren: Diffie-Hellmann und ElGamal
 Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
 Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
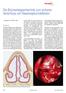 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
2 Kurzeinführung in die Programmiersprache C 2.7 Programmstruktur & Module. 2 Kurzeinführung in die Programmiersprache C 2.7 Programmstruktur & Module
 2 Kurzeinführung in die Progrmmiersprche C 2.7 Progrmmstruktur & Module 10 Werteustusch zwischen Funktionen Mechnismus Aufrufer Funktion Funktion Aufrufer Prmeter j mit Hilfe von Zeigern Funktionswert
2 Kurzeinführung in die Progrmmiersprche C 2.7 Progrmmstruktur & Module 10 Werteustusch zwischen Funktionen Mechnismus Aufrufer Funktion Funktion Aufrufer Prmeter j mit Hilfe von Zeigern Funktionswert
Kapitel 1. Anschauliche Vektorrechnung
 Kpitel 1 nschuliche Vektorrechnung 1 2 Kpitel I: nschuliche Vektorrechnung Montg, 13. Oktoer 03 Einordnung Dieses erste Kpitel ht motivierenden Chrkter. Es führt n die geometrische nschuung nknüpfend die
Kpitel 1 nschuliche Vektorrechnung 1 2 Kpitel I: nschuliche Vektorrechnung Montg, 13. Oktoer 03 Einordnung Dieses erste Kpitel ht motivierenden Chrkter. Es führt n die geometrische nschuung nknüpfend die
Mechanismus Aufrufer Funktion Funktion Aufrufer Parameter ja mit Hilfe von Zeigern Funktionswert nein ja globale Variablen ja ja
 2 Kurzeinführung in die Progrmmiersprche C 2.7 Progrmmstruktur & Module 10 Werteustusch zwischen Funktionen Mechnismus Aufrufer Funktion Funktion Aufrufer Prmeter j mit Hilfe von Zeigern Funktionswert
2 Kurzeinführung in die Progrmmiersprche C 2.7 Progrmmstruktur & Module 10 Werteustusch zwischen Funktionen Mechnismus Aufrufer Funktion Funktion Aufrufer Prmeter j mit Hilfe von Zeigern Funktionswert
Computer Vision Group Prof. Daniel Cremers. Fließkomma-Arithmetik und Fehlerfortpflanzung
 Computer Vision Group Prof. Dniel Cremers Fließkomm-Arithmetik und Fehlerfortpflnzung Fließkomm-Arithmetik Definition einer Mschinenopertion: 1. Berechne für Mschinenzhlen ds Ergenis der Opertion mit höherer
Computer Vision Group Prof. Dniel Cremers Fließkomm-Arithmetik und Fehlerfortpflnzung Fließkomm-Arithmetik Definition einer Mschinenopertion: 1. Berechne für Mschinenzhlen ds Ergenis der Opertion mit höherer
Automaten, Spiele, und Logik
 Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Themenbereich: Kongruenzsätze Seite 1 von 6
 Themenereich: Kongruenzsätze Seite 1 von 6 Lernziele: - Kenntnis der genuen Formulierung der Kongruenzsätze - Kenntnis der edeutung der Kongruenzsätze - Fähigkeit, die Kongruenzssätze gezielt zur egründung
Themenereich: Kongruenzsätze Seite 1 von 6 Lernziele: - Kenntnis der genuen Formulierung der Kongruenzsätze - Kenntnis der edeutung der Kongruenzsätze - Fähigkeit, die Kongruenzssätze gezielt zur egründung
Bruchterme. Franz Embacher
 mthe online Skripten http://www.mthe-online.t/skripten/ Bruchterme Frnz Emcher Fkultät für Mthemtik der Universität Wien E-mil: frnz.emcher@univie.c.t WWW: http://homepge.univie.c.t/frnz.emcher/ In diesem
mthe online Skripten http://www.mthe-online.t/skripten/ Bruchterme Frnz Emcher Fkultät für Mthemtik der Universität Wien E-mil: frnz.emcher@univie.c.t WWW: http://homepge.univie.c.t/frnz.emcher/ In diesem
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
 S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
9 Das Riemannsche Integral
 1 9 Ds Riemnnsche Integrl 9.1 Definition und Beispiele Sei I = [, ] R mit
1 9 Ds Riemnnsche Integrl 9.1 Definition und Beispiele Sei I = [, ] R mit
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
Einführung in die Lineare Algebra
 Einführung in die Linere Alger Linere Gleichungssysteme Dieses Kpitels dient zur Motivtion und Vorereitung der systemtischen Drstellung. Wir hen dfür ds wichtigste Prolem der elementren lineren Alger gewählt,
Einführung in die Linere Alger Linere Gleichungssysteme Dieses Kpitels dient zur Motivtion und Vorereitung der systemtischen Drstellung. Wir hen dfür ds wichtigste Prolem der elementren lineren Alger gewählt,
2. Klausur in K2 am
 Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
1. Klausur zur Vorlesung Informatik III Wintersemester 2004/2005
 Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2004/05 ILKD Prof. Dr. D. Wgner 24. Ferur 2005 1. Klusur zur Vorlesung Informtik III Wintersemester 2004/2005 Lösung! Bechten Sie: Bringen
Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2004/05 ILKD Prof. Dr. D. Wgner 24. Ferur 2005 1. Klusur zur Vorlesung Informtik III Wintersemester 2004/2005 Lösung! Bechten Sie: Bringen
Übungsblatt 4 - Lösung
 Formle Sprchen und Automten Üungsltt 4 - Lösung 26. M 2013 1 Whr oder flsch? Begründe kurz dene Antwort! 1. In enem determnstschen endlchen Automten gt es für jedes Wort w Σ mxml enen kzepterenden Pfd.
Formle Sprchen und Automten Üungsltt 4 - Lösung 26. M 2013 1 Whr oder flsch? Begründe kurz dene Antwort! 1. In enem determnstschen endlchen Automten gt es für jedes Wort w Σ mxml enen kzepterenden Pfd.
Einführung in die Integralrechnung
 Einführung in die Integrlrechnung Einführung in die Integrlrechnung Einführung in die Integrlrechnung In der Differentilrechung estnd die ufge u drin, zu einer gegeenen Funktion f deren leitungsfunktion
Einführung in die Integrlrechnung Einführung in die Integrlrechnung Einführung in die Integrlrechnung In der Differentilrechung estnd die ufge u drin, zu einer gegeenen Funktion f deren leitungsfunktion
Grundwissen Mathematik 8.Klasse Gymnasium SOB. Darstellung im Koordinatensystem: Der Kreisumfang ist direkt proportional zu seinem Radius.
 Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Gymso 1 Grundwissen Mthemtik 8.Klsse Gymnsium SOB 1.Funktionle Zusmmenhänge 1.1.Proportionlität Ändern sih ei einer Zuordnung die eiden Größen im gleihen Verhältnis, so spriht mn von einer direkten Proportionlität.
Falls die Werte von X als Ergebnisse eines Zufallsvorgangs resultieren, wird X zu einer stetigen Zufallsvariable.
 Sttistik I für Sttistiker, Mthemtiker und Informtiker Lösungen zu Bltt 11 Gerhrd Tutz, Jn Ulbricht, Jn Gertheiss WS 7/8 Theorie: Stetige Zufllsvriblen Begriff Stetigkeit: Eine Vrible oder ein Merkml X
Sttistik I für Sttistiker, Mthemtiker und Informtiker Lösungen zu Bltt 11 Gerhrd Tutz, Jn Ulbricht, Jn Gertheiss WS 7/8 Theorie: Stetige Zufllsvriblen Begriff Stetigkeit: Eine Vrible oder ein Merkml X
Protokoll zur Vorlesung Theoretische Informatik I
 Protokoll zur Vorlesung Theoretishe Informtik I! " # $ % # & ' ( % ) * + & " & & &, " ' % + - + # + & '. / 0 1 # 0 & 2 & # & 3 4 & 5 # 0 + & 6 & ' + 7 7 3 8 4 & 7 + + + % ( % 6 # 9 & 5 # 0 + & 3 8. : &
Protokoll zur Vorlesung Theoretishe Informtik I! " # $ % # & ' ( % ) * + & " & & &, " ' % + - + # + & '. / 0 1 # 0 & 2 & # & 3 4 & 5 # 0 + & 6 & ' + 7 7 3 8 4 & 7 + + + % ( % 6 # 9 & 5 # 0 + & 3 8. : &
7.4. Teilverhältnisse
 7... erehnung von Teilverhältnissen ufgen zu Teilverhältnissen Nr. 7.. Teilverhältnisse Die Shwerpunkte von Figuren und Körpern lssen sih mit Hilfe von Teilverhältnissen usdrüken und erehnen. Definition
7... erehnung von Teilverhältnissen ufgen zu Teilverhältnissen Nr. 7.. Teilverhältnisse Die Shwerpunkte von Figuren und Körpern lssen sih mit Hilfe von Teilverhältnissen usdrüken und erehnen. Definition
Orientierungstest Mathematische Grundlagen
 Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
- 1 - VB Inhaltsverzeichnis
 - - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
Inhaltsverzeichnis. Inhaltsverzeichnis... 1 3.Logik... 2. 3.1 Zahlensysteme... 2. 3.2 Grundbegriffe zweiwertiger Logik... 13
 Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit bietet, ihre statistischen Meldungen über das Internet auszufüllen und einzureichen.
 Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mathematik fu r Ingenieure (Maschinenbau und Sicherheitstechnik) 2. Semester Apl. Prof. Dr. G. Herbort Dr. T. Pawlaschyk. SoSe16 Arbeitsheft Blatt 3
 Mthemtik fu r Ingenieure (Mschinenu und Sicherheitstechnik). Semester Apl. Prof. Dr. G. Herort Dr. T. Pwlschyk SoSe6 Areitsheft Bltt Hinweis: Besuchen Sie die Vorlesung und vervollst ndigen Sie Areitsheft.
Mthemtik fu r Ingenieure (Mschinenu und Sicherheitstechnik). Semester Apl. Prof. Dr. G. Herort Dr. T. Pwlschyk SoSe6 Areitsheft Bltt Hinweis: Besuchen Sie die Vorlesung und vervollst ndigen Sie Areitsheft.
Kurvenintegrale. 17. Juli 2006 (Korrigierte 2. Version) 1 Kurvenintegrale 1. Art (d.h. f ist Zahl, kein Vektor)
 Kurvenintegrle Christin Mosch, Theoretische Chemie, Universität Ulm, christin.mosch@uni-ulm.de 7. Juli 26 (Korrigierte 2. Version Kurvenintegrle. Art (d.h. f ist Zhl, kein Vektor Bei Kurvenintegrlen. Art
Kurvenintegrle Christin Mosch, Theoretische Chemie, Universität Ulm, christin.mosch@uni-ulm.de 7. Juli 26 (Korrigierte 2. Version Kurvenintegrle. Art (d.h. f ist Zhl, kein Vektor Bei Kurvenintegrlen. Art
4 Die rationalen Zahlen
 4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
Monte-Carlo-Integration
 Monte-Crlo-Integrtion von Dietmr Herrmnn, Anzing Kurzfssung: An Hnd eines einfchen Beispiels wird gezeigt, dß jedes Integrl ls Erwrtungswert einer reellen Zufllsgröße ufgefßt werden knn. een einer symptotischen
Monte-Crlo-Integrtion von Dietmr Herrmnn, Anzing Kurzfssung: An Hnd eines einfchen Beispiels wird gezeigt, dß jedes Integrl ls Erwrtungswert einer reellen Zufllsgröße ufgefßt werden knn. een einer symptotischen
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
5. Vektor- und Matrizenrechnung
 Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
Programmieren in C/C++ und Matlab
 Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Übungen zur Vorlesung Grundlagen der Mathematik II Lösungsvorschlag
 MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner SS 2015 Bltt 6 26.05.2015 Üungen zur Vorlesung Grundlgen der Mthemtik II Lösungsvorschlg 21. ) Ein Qudrt mit der Seitenlänge + und dmit dem
MATHEMATISCHES INSTITUT DER UNIVERSITÄT MÜNCHEN Dr. E. Schörner SS 2015 Bltt 6 26.05.2015 Üungen zur Vorlesung Grundlgen der Mthemtik II Lösungsvorschlg 21. ) Ein Qudrt mit der Seitenlänge + und dmit dem
JUSTUS-LIEBIG-UNIVERSITÄT GIESSEN
 JUSTUS-LIEBIG-UNIVERSITÄT GIESSEN Professur für VWL II Wolfgng Scherf Die Exmensklusur us der Volkswirtschftslehre Erschienen in: WISU 8-9/2000, S. 1163 1166. Fchbereich Wirtschftswissenschften Prof. Dr.
JUSTUS-LIEBIG-UNIVERSITÄT GIESSEN Professur für VWL II Wolfgng Scherf Die Exmensklusur us der Volkswirtschftslehre Erschienen in: WISU 8-9/2000, S. 1163 1166. Fchbereich Wirtschftswissenschften Prof. Dr.
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Lineare DGL zweiter Ordnung
 Universität Duisburg-Essen Essen, 03.06.01 Fkultät für Mthemtik S. Buer C. Hubcsek C. Thiel Linere DGL zweiter Ordnung Betrchten wir ds AWP { x + x + bx = 0 mit, b, t 0, x 0, v 0 R. Der Anstz xt 0 = x
Universität Duisburg-Essen Essen, 03.06.01 Fkultät für Mthemtik S. Buer C. Hubcsek C. Thiel Linere DGL zweiter Ordnung Betrchten wir ds AWP { x + x + bx = 0 mit, b, t 0, x 0, v 0 R. Der Anstz xt 0 = x
Dr. Günter Rothmeier Kein Anspruch auf Vollständigkeit Elementarmathematik (LH) und Fehlerfreiheit
 Nturwissenschftliche Fkultät I Didktik der Mthemtik Privte Vorlesungsufzeichnungen Kein Anspruch uf Vollständigkeit 5 7 Elementrmthemtik (LH) und Fehlerfreiheit. Zhlenereiche.4 Die Reellen Zhlen.4.. Definition
Nturwissenschftliche Fkultät I Didktik der Mthemtik Privte Vorlesungsufzeichnungen Kein Anspruch uf Vollständigkeit 5 7 Elementrmthemtik (LH) und Fehlerfreiheit. Zhlenereiche.4 Die Reellen Zhlen.4.. Definition
1.1 Grundlagen: Reguläre Ausdrücke
 11 Grundlgen: Reguläre Ausdrücke Progrmmtext enutzt ein endliches Alphet Σ von Einge-Zeichen, zb ASCII :-) Die Menge der Textschnitte einer Token-Klsse ist i regulär Reguläre Sprchen knn mn mithile regulärer
11 Grundlgen: Reguläre Ausdrücke Progrmmtext enutzt ein endliches Alphet Σ von Einge-Zeichen, zb ASCII :-) Die Menge der Textschnitte einer Token-Klsse ist i regulär Reguläre Sprchen knn mn mithile regulärer
Kapitel: Endliche Automaten & reguläre Sprachen. Endliche Automaten und reguläre Sprachen 1 / 125
 Kpitel: Endliche Automten & reguläre Sprchen Endliche Automten und reguläre Sprchen 1 / 125 Endliche Automten Endliche Automten erluen eine Beschreiung von Hndlungsläufen: Wie ändert sich ein Systemzustnd
Kpitel: Endliche Automten & reguläre Sprchen Endliche Automten und reguläre Sprchen 1 / 125 Endliche Automten Endliche Automten erluen eine Beschreiung von Hndlungsläufen: Wie ändert sich ein Systemzustnd
Hans Walser. Geometrische Spiele. 1 Vier gleiche rechtwinklige Dreiecke. 1.1 Allgemeiner Fall
 Hns Wlser Geometrische Spiele 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fll Wir strten mit einem elieigen rechtwinkligen Dreieck in der ülichen Beschriftung. A c B Strtdreieck C Nun versuchen
Hns Wlser Geometrische Spiele 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fll Wir strten mit einem elieigen rechtwinkligen Dreieck in der ülichen Beschriftung. A c B Strtdreieck C Nun versuchen
UNTERRICHTSPLAN LEKTION 22
 Lektion 22 Am esten sind seine Schuhe! UNTERRICHTSPLAN LEKTION 22 1 Wohin geht er wohl? Gruppenreit, Die Bücher sind geschlossen. In Kleingruppen smmeln die TN Feste und Prtys, zu denen mn esondere Kleidung
Lektion 22 Am esten sind seine Schuhe! UNTERRICHTSPLAN LEKTION 22 1 Wohin geht er wohl? Gruppenreit, Die Bücher sind geschlossen. In Kleingruppen smmeln die TN Feste und Prtys, zu denen mn esondere Kleidung
FORMALE SYSTEME. 6. Vorlesung: Reguläre Ausdrücke. TU Dresden, 27. Oktober Markus Krötzsch
 FORMALE SYSTEME 6. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 27. Oktober 2016 Rückblick Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 2 von 29 Wiederholung: Opertionen uf Automten
FORMALE SYSTEME 6. Vorlesung: Reguläre Ausdrücke Mrkus Krötzsch TU Dresden, 27. Oktober 2016 Rückblick Mrkus Krötzsch, 27. Oktober 2016 Formle Systeme Folie 2 von 29 Wiederholung: Opertionen uf Automten
a) Potenzieren ausgesprochen als Beispiel a b = c a = Basis a hoch b = c 4 3 = 64 b = Exponent c = Potenzwert
 8. Potenzen 8. Einführung in Potenzen / Wurzeln / Logrithmen Neen den klssischen Grundrechenopertionen git es weitere Opertionen, welche Beziehungen zwischen Zhlen schffen: Potenzieren Rdizieren Wurzelziehen)
8. Potenzen 8. Einführung in Potenzen / Wurzeln / Logrithmen Neen den klssischen Grundrechenopertionen git es weitere Opertionen, welche Beziehungen zwischen Zhlen schffen: Potenzieren Rdizieren Wurzelziehen)
