Modul Investition. Einzahlungen Kredite wirtschaftlicher Absatzmarkt
|
|
|
- Ursula Bergmann
- vor 8 Jahren
- Abrufe
Transkript
1 Modul Ivesiio. Leisugs- ud Fiazeeich de Ueehmug Eilage uszahluge Eigekapial- Realivesiioe Beschaffugsmak gee usschüuge (Leisugswischafliche Beeich) Fiaz- Eizahluge Kedie wischafliche sazmak Femdkapial- Beeich des gee Zis/Tilgug Ueehmes Eizahluge Saa Suveioe Fiazivesiioe uszahluge Kapialmak Seue Fiazieug Ivesiio Ueehme. Zusammesezug des Vemöges Zusammesezug des Vemöges is esimm duch: - Kapialvewedugsescheiduge i de Vegagehei - Kapialvewedugsescheiduge i de Gegewa Sukuvemöge: lag ud mielfisige Kapialalage - Sachalage, Fiazalage, immaeielle lagegüe - Umlaufvemöge mi Kapialidug > Jah Ivesiios- ud Wischaflichkeisechuge zu Emilug de Reailiä ud Besimmug de Voeilhafigkei vo Ivesiiospojeke Umlaufvemöge: - Posiioe mi kuzfisige Kapialidug < Jah! Kassehalugssyseme zu ufechehalug de Liquidiä hp://wlladshu.ipod.com
2 De Ivesiiosegiff Zielgeichee Eisaz fiazielle Miel zu Beschaffug vo Güe des Sukuvemöges, egied mi eie uszahlug ud eie ode mehee zuküfige (usichee) ud ewaugsgemäß höheweige Eizahluge aus de Veweug. kiva Bilaz Passiva lagevemöge Eigekapial esadsoieie Umlaufvemöge Femdkapial Mielvewedug Mielhekuf zahlugs- Ivesiio Fiazieug oieie Beschaffug Podukio saz. Ivesiiosae Ivesiio Sachivesiio Fiazivesiio Es-/Eiichugs- Esazivesiio Eweieugsivesiio Ivesiio Ideische Esaz Raioalisieugsivesiio 3. Ivesiio als Escheidugspozeß hp://wlladshu.ipod.com
3 Willesildug Willesduchsezug egug Uesuchug uswahl/escheidug Realisaio Koolle Ivesiiosechevefahe saisch ue ahme zu isoliee vo Sichehei Beweug vo Ivesiioe dyamisch ue Beücksichigug zu Beweug vo mehweige Ivesiios-/ Ewauge Fiazieugspogamm Fiazwischafliche Disposiio des Umlaufvemöges Wokig Capial: Vemögeseile, die sich iehal eies Jahes im Rahme des Umsazpozesses wiede i liquide Miel zuückvewadel. Voäe Kasse Podukioszyklus ud Vemögesumschichug Fodeuge Wokig Capial: hp://wlladshu.ipod.com 3
4 Beag WC flukuieedes WC - egi sich aus Umsazspize - ezieh sich de miel- ode lagfisige Kapialedafsplaug - Polem de opimale Kassehalug Pemaees WC Zei Kassehalugspolem: Kasse: Besad a Geld aus Kedigewähug ode eigee Miel - Bageld - Buchgeld auf Bak- ud Posscheckkoe Kassehalugsheoie vo Keyes: - Tasakiosmoiv: Deckug laufede uszahlugsedafe - Vosichsmoiv: usgleich vo Pogoseugeauigkeie (flukuieedes WC) - Spekulaiosmoiv: Nuzug güsige lagemöglichkeie e: - Kassehalugsheoie vo Keyes veachlässig die Ueehmesziele Gewi zw. Reailiä - Modee Geldmak- ud Kediisumee däge Kassehalugsmoive vo Keyes i de Hiegud, weil Vezisug ud Liquidiä gewähleise wede (Nea-Moey-sses: Ceificaes of Deposi, Commecial Papes) Ziel: Opimale Liquidiä ei Beachug de Ueehmesziele Gewi- zw. Reailiäsmaximieug max. Zissaldo ei Efüllug de efodeliche uszahluge Folge: usichug de Kassedisposiio a de fiazwischafliche Ueehmesziele Cash Maageme: - ich eöiges Kapial wid zu eiem möglichs hohe Zissaz ageleg ud ka zu Tilgug eie fällige Veidlichkei ahezu kosefei liquidie wede. - Kasse wid ich vezis ud is deswege möglichs geig zu hale Kassedisposiio is deshal ei weseliche Besadeil de kuzfisige Fiazplaug. Opimieug des Kassehalugsesades is spezielles Lagehalugspolem (vgl. Modelle fü opimale Lagehalug) hp://wlladshu.ipod.com 4
5 Zusäzlich: akive Gesalug de Zahlugsvogäge - Beschleuigug de Eizahluge: Rechugssellug, Zahlugsvekeh - Vezögeug de uszahluge: chug!!! Repuaio des Ueehmes Cash Maageme Syseme: - EDV-gesüze Kommuikaio zwische Bake ud Geschäfskude - usausch vo Dae zu ägliche Seueug de Kassedisposiio - Balace Repoig: elekoische Kooauszug - Moey Tasfe: elekoische wicklug des Zahlugsvekehs - Poolig: Zusammefassug mehee Koe zu Zisfessezug - Neig: Zusammefassug kozeiee Fodeuge ud Veidlichkeie 3. Disposiio des Fodeugsesades Höhe des Fodeugsesades eeifluß duch: - Umsaz - Zahlugs- ud Kedikodiioe - Hadhaug Mah- ud Ikassowese Gefah des Kapialveluses duch Fodeuge: - Fiazieugskose: sowei kei Eigekapial muß Femdkapial aufgeomme wede - Vewalugskose, Ikassokose - Kose des mögliche Fodeugsausfalls Fodeug de Fiazwischaf: möglichs kleie Fodeugsesad e: Makeiggesichspuke ud Hadelskoveioe Folge fü Fiazplaug ud Kassedisposiio: Koolle de Veweildaue de Fodeuge 4. Lagehalug: Escheidugspolem de Fiazwischaf Lagehalug ide fiazielle Miel, Fiazieugskose esehe e: - zu kleie Voashalug ig Gefah de Fehlmegekose ei Podukiosausfälle - Gößee Besellmege ige essee Bezugskodiioe Lösug: eieswischafliche Lagehalugsmodelle eiseze Veigeug des Lageesades eziel Kapialfeisezugseffek Fiazieug duch Vemögesumschichuge e: kuzfisige liquidiäspoliische Eigiffe u eschäk möglich, da Veäußeugsmöglichkeie vom sazmak ahäge hp://wlladshu.ipod.com 5
6 - Veäußeug vo Feigezeugisse ue Makpeis u kuzfisig, sos efolgswischafliche Eiuße. - Podukio ue au des Besads a Halfeigfaikae Sysemaisieug Zahlugsmiel ud Zahlugsvekeh (siehe Olfe) Ivesiiosechevefahe. Kuzüelick üe die saische Vefahe Saische Vefahe Eipeiodemodelle ei Sichehei - kalkulaoische Vefahe: i de Regel wede Kose ud Elöse eücksichig - Hilfs- ud äheugsvefahe, Duchschispeiode als Basis - ukomplizie, mi geige Kose aweda Folge: och i goßem Umfag agewad Nacheile: - kuzfisige Beachugsweise, of wid u das ese Jah ach de schaffug eies Ivesiiosojeks eache ud fü Folgejahe als kosa uesell (schwakede Mege ud Peise fü Beschaffug ud Umschlag) - achfolgede Kose(z.B. Isadhalugsaufwad) wid ich eücksichig - das Ivesiiosojek wid isolie eache, ohe Iedepedeze mi esehede ode küfige Ivesiiosojeke zu eleuche - Zeipäfeeze de Üeschüsse wede auch ei de Deailaalyse de gesame Nuzugsdaue ich eücksichig (Höhe de Rückflüsse) - Usichehei zuküfige Dae ud Göße wede i de Regel ich eücksichig Kosevegleichsechug - Beueilug de elaive Voeilhafigkei eies Ivesiiosojekes ausschließlich ahad de Kose (Zeale Kosekompoee: Peiode- ode Sückkose; fixe ode vaiale Kose, Kapialkose ode Beieskose) - wedug: uswahl- ud Esazpoleme ei kleiee Esaz- ud Raioalisieugsescheiduge im Sie eie Wischaflichkeisaalyse - Elöse, Gewi ode Reailiäsgöße wede ich heagezoge Escheidugskieie: Kose IO >< Kose IO Gewivegleichsechug - Basis: Kosevegleichsechug; zusäzlich: Eiezug vo Elöse - wedug: voallem Beueilug vo Eweieugsivesiioe - leaivevegleich u ichig, we Laufzei ud Kapialeisaz gleich Escheidugskieie: Gewi IO >< Gewi IO woei Gewi IO, IO > hp://wlladshu.ipod.com 6
7 Reailiäsechug (Reu o Ivesme /RoI) # Beueilug de asolue Voeilhafigkei eizele IO mi ueschiedlich hohe Kapialeisäze ahad ihe Redie zw. Reaailiä # Beücksichigug ueschiedliche Nuzugsdaue ud Kapialeisäze miels Diffeezivesiioe # Maßsa fü duchschiliche (iee) Vezisug eies IO Duchschisvezisug des im IO duchschilich geudee Kapials # Buo-/Neoedie: Beücksichigug/Nich-Beücksichigug kalkulaoische Zise # wedug: Escheiduge üe Raioalisieugsivesiioe sowie Neu- ud Esazivesiioe # Escheidugskieie: - Voeilhafigkeisescheidug: Reailiä IO > gewüsche Mideseailiä - Wahlpolem: Reailiä IO >< Reailiä IO - Esazpolem: Reailiä IO al >< Reailiä IO eu # Reailiäe (chug eigesezes Kapial ud Gewi) moisaiosechug (Pay-Back-(Off-/Ou-) Rechug) # Basis: Ei- ud uszahluge ue Beücksichigug de Zei, i de sich die schaffugskose eies IO üe die Elöse amoisie hae Gedaklich wede die Rückflüsse zuächs ausschließlich fü die moisaio vewede. - moisaiosdaue: Zeiaum, i dem de Kapialeisaz des IO wiede zuückfließ - moisaioszeipuk: Zeipuk zu dem de Kapialeisaz die IO eaglich wiede voll wiedegewoe wude ud a dem weiee Fiazmielückflüsse fü adee Vewedugszwecke zw. zu Kapialvezisug zu Vefügug sehe. # Vesuch Risiko ud Liquidiäsauswikuge eie Ivesiio azuschäze: Je läge die Kapialidug i eiem IO, deso höhe is i de Regel sei Risiko # Keie Beücksichigug de Wischaflichkei vo IO sowie de Weeweguge ach de moisaioszei # wedug: uswahl- ud Esazpoleme ei IO mi gleiche Nuzugsdaue; häufig als Egäzug zu Reailiäsechug Duchschisvefahe Voaussezug id gleichleiede peiodische Rückflüsse des IO moisaioszei Kapialeisaz Resweelös / duchschiliche Rückfluß (Cash-flow) Kumulaiosvefahe: ddiio de effekive jähliche Rückflüsse is zu dem Jah, i dem die Höhe des Kapialeisazes eeich wid Escheidugskieie: - Voeilhafigkeisescheidug: moisaiosdaue IO < maximal gewüsche moisaiosdaue - Wahlpolem: moisaiosdaue IO >< moisaiosdaue IO moisaioszeipuk IO >< moisaioszeipuk IO moisaiosechug solle um Reailiäsechug egäz wede. hp://wlladshu.ipod.com 7
8 Dyamische Vefahe I.Gudlage. Begiffe Ivesiiosojek IO uoomes Kapialalageojek Ivesiio u, we IO voeilhaf Zahlugseihe ZR Zusammefassede Dasellug alle mi eiem IO veudee Eizahluge ud uszahluge. llgemei: Dimesio eie Zahlug - Höhe - Zeipuk - Sicheheisgad Eizahluge: uszahluge: Neoeizahluge: e a ZR: 3... IO 3... Koveioe: - Plaugszeiaum: eachee Zeiaum - lle Zahluge falle am Peiodeede a - e (posiiv i de Regel) - a - auch: (egaiv i de Regel) Escheidugszeipuk is - Zeipuk zu dem fällig is - Begi de Peiode, die am fag vo ede - Ede de Vopeiode Beache: u Zahluge wede eache - keie fa - keie kalkulaoische Kose - keie Resuchwee (RWB) ae: evl. Resvekaufselöse. Basis Kapialmakmodell Kapialmak KM Seh fü: - sämliche Geschäfe de Kapialalage i Fiazivesiioe - Weiegae des Kapials als EK ode FK hp://wlladshu.ipod.com 8
9 Teileeiche: - Kedimak - kiemak - Reemak Vollkommee Kapialmak VKM lieg vo, we gil: - vollkommee Ifo alle Makeilehme Homogee Ewauge - keie Tasakioskose TK - keie Seue - alle Teilehme - hadel aioal - eagiee uedlich schell - hae keie Eifluß auf de Zissaz!. Eiheiliche Zissaz i i V lagezissaz Veschuldugszissaz!. Mielalage i elieige Höhe möglich! 3. Mielaufahme i elieige Höhe möglich Uvollkommee Kapialmak UVKM! mideses eie ahme vo VKM is velez! Tasakioskose! keie homogee Ewauge! i i V Mielalage ud aufahme köe eschäk sei 3. Zisechug Duch Zise köe ZR auf - eie Beag - eie Zeipuk vediche wede. Zis Peis fü die Üelassug eie Geldeihei auf Zei Fukioe des Zises:. usduck fü Zeipäfeeze. usduck fü Liquidiäspäfeeze 3. usduck fü Oppouiäskose 4. usduck fü Risikopäfeez Zu./.: Geld heue wid höhe eigeschäz als Geld späe Zu 3.: Zis Peis fü de Vezich auf aleaive Nuzugsmöglichkeie des Geldes - Eschädigug fü Kosumvezich - Eschädigug fü egagee Gewimöglichkeie Zu 4.: höhees Risiko Iveso fode höhee Zissaz hp://wlladshu.ipod.com 9
10 Spaeilage TDM ; i, Guhae i 3?. Jah : V *i *(i) *,. Jah : V V V * i V (i) *(i)*(i) * (i) * (,) 3. Jah: V 3 V V * i (i) 3 33 llgemei: V * (i) ufzisugsfako 4. Vollsädige Fiazpla Fiazpla FP Isume zu - zukufsezogee - emigeaue - vollsädige Efassug alle elevae Ei- ud uszahluge Gleiche Koveioe wie ei ZR Vogehesweise: - Dae efasse - Plaugszeiaum feslege - Relevae Göße fesselle - Emilug de ZR FiZR NeoZR zw EZÜ Ojekzahlugseihe Fiazieugszahlugseihe Eizahlugsüeschüsse Ziel: Komplexiäsedukio duch Saldieug II. Kapialwemehode KWM. Begiffe llgemei: Kapialwe Bawe vo Zahluge BKW Buokapialwe Bawe alle Zahluge a Neokapialwe BKW schaffugsauszahluge Ziele KWM: ussage üe Voeilhafigkei IO fide Loh sich ei IO? Kieium: BKW > > Vegleichakei vo IO hp://wlladshu.ipod.com
11 . Kapialwe ud VKM Defiiio: BKW * (i) - - BKW - * (i) Pämisse: - Bedeuug VKM - Reivesiiospämisse feiwedede Beiäge köe jedezei zum KZF vewede wede KZF i (Kalkulaioszisfuß) Redie de ese leaive, die jedezei wähed des gesame Beachugszeiaums fü Kapialalage ud Kediaufahme zu Vefügug seh. (VKM! i i V ) Escheidugskieium ei KWM is KZF auf VKM is die Makedie Beispiele:. KW eie Zahlug i 4 464, ; i, BKW *(i) - 4 *(,) 4 464,/,4. Eizahluge - 3 jeweils e ; i, ZR 3? Bawe? 3 BKW (i) (i) (i) 3 (i) 3 *, - *, - *, -3 99,9 86,44 75,3 486,85 hp://wlladshu.ipod.com
12 . KWM ud Voeilhafigkei KWM: is de implizie Vegleich mi de leaive, dee Redie als KZF vewede wid. Redie IO >< Redie de ese leaive Bese leaive auf VKM is die Kapialmakalage (KM) zu i Vogehesweise: üe we > IO voeilhaf Vegleich:. am KM alege Redie KZF i. i IO alege Egeis: > Redie IO > KZF Redie IO KZF < Redie IO < KZF is asolues Maß fü Voeilhafigkei Exkus: -Fukio es gil: je göße i deso kleie Beispiel: ( i) ZR, i i, 8*, 5 *, 7,73 4,3 4,5 i,5 8*,5 5 *,5 69,56 37,8 7,37 hp://wlladshu.ipod.com
13 is eie fallede Fukio des KZF dkzf di < i Wie hoch is de eie KM? i,, lageeag ZR 3, - uszahlug Eizahlug (Zise wede sofo eigezahl) *( ) *(,) *(,) 3 I ZR wid mi Kapialmakzis aufgezis, eim wid da mi demsele KMZ agezis. eie KM is imme eie Kapialaufahme is imme llgemei: Diskoie ma eie ZR mi ihe eigee Redie, is de imme (Ma vegleich eie Kapialalage mi sich sels) hp://wlladshu.ipod.com 3
14 Beispiele: IO i i V, ZR I, II, I *, *,...,4 II 6 5, llgemei: BKW eie uifome ZR Gudsäzlich: Schließe sich IO ich gegeseiig aus, köe auf VKM alle IO ealisie wede, weil die Kediaufahme ueschäk möglich is..3 KWM ud Ragfolgeescheiduge Poleme: i.uszahlugsdiffeeze.ueschiedliche Zahlugssuku 3.Ueschiedliche Laufzei Zu./3. uf VKM kei Polem, weil ZR duch Diskoieug auf eie We zu eiem esimme Zeipuk vediche wid. Zu. Nu ei IO ka ealisie wede echische leaive Diffeezivesiio KM... IO II KM , IOII KM gleiches Egeis wie oe Diffeez auf VKM kei Polem, weil - Mielalage u zu i KM-Redie möglich - Zahlugseihe wid mi i KM-Redie diskoie KM hp://wlladshu.ipod.com 4
15 auf VKM köe alle ZR polemlos mieiade vegliche wede I > II IO I f IO II Päfeezzeiche Femdfiazieug - Iveso ka eie Kedi zu Kose i. H. v. i v aufehme - Tilgugsae. Raeilgug. Edfällige Tilgug 3. Zeood-Tilgug 4. uiäische Tilgug 5. Tilgug gem. EZÜ 6. elieige Tilgug zu. Rae leie gleich zu. Tilgug am Ede de Laufzei - jähliche Ziszahluge zu 3. - keie laufede Ziszahluge - Tilgug kumuliee Zis am Laufzeiede hp://wlladshu.ipod.com 5
16 zu 4. - Zis Tilgug kosa - seigede Tilgugseiäge - fallede Ziszahluge zu 5. - jähliche Ziszahluge - alle vefügae esliche Eizahlugsüeschüsse (EZÜ) zu Tilgug des Kedis zu 6. - ülicheweise jähliche Ziszahluge - kei ypisches Tilgugsmuse Beispiel: i i V FF edfällige Tilgug 3 4, F i*f T 4 - NZR 4-57 FF i, *, *, 4*, 3 57*, 4,9 gleiches Egeis wie ei vollsädige Eigefiazieug (EF) hp://wlladshu.ipod.com 6
17 . FF Tilgug gemäß EZÜ allg. T (i V *F - ) 3 4, F i*f ,7 (F ) [] [9] [77] [347] [] T ,3 FF, Ti lg. gemezü 4 i, 48,3*,,9 gleiches Egeis wie ei EF Ielevaz de Fiazieug auf VKM waum: KWM füh auf VKM imme zum ichige ud gleiche Egeis, da i de elevae KZF is i i i V Kapialaussaug des Ivesos is ieleva auf VKM sid - ZF - Fi Fiazieugso Tilgugssuku ieleva fü Besimmug de Voeilhafigkei eies IO Gud: de KM hp://wlladshu.ipod.com 7
18 .4 Ielevazhese.4. Ielevaz de Zielfukio Zielfukio ZF:. Vemögesmaximieug - : Bawemaximieug V - : Edwemaximieug V - zu eiem elieige Zeipuk: Edwemax. zu m Zeipuk x V x. Eikommesmaximieug Zielgöße: uifomes Eikomme im Plaugszeiaum ZF: wähle IO mi dem höchse uifome Eikomme im Plaugszeiaum Zweck: Beueilug de Voeilhafigkei z.b. Iveso möche i veeise Bawemax. Iveso B möche i veeise Edwemax. i % IO: I, II, Kalkül Iveso : I, II, B,9 > > IO I ealisiee, falls IO I ud IO II echische leaive Kalkül Iveso B: V V escheided: 4 I, B 4 II, B *, *, 6 6 *, 6 *, *, 6 *, 3 3 *, 5 *, 4 4 6, 48,3 46,4 hp://wlladshu.ipod.com 8
19 aleaive Beechug: V V I, B 4 II, B 4 I * ( i) II 4 * ( i),9*, 4 *, ,3 46,4 V I, B 4 > V II, B 4 IO I ealisiee we I ud II ech. leaive gleiches Egeis oz ueschiedliche Zielfukioe Ielevaz de Zielfukio auf VKM Waum? alle uf- ud zisuge wede mi dem KZF i vogeomme Ragfolge ach Bawee i ka ich vo de Ragfolge ach Edwee aweiche füh auf VKM imme zum ichige Egeis ZF: - Maß fü Voeilhafigkei - Kieium fü Ragfolge is ieleva.4. Ielevaz de Fiazieug (Kapial- ud Tilgugssuku) Gudsäzlich: KWM is - ei vollsädige Eigefiazieug EF (F ) - ei vollsädige Femdfiazieug FF (F ) - ei Mischfiazieug MF (F < ) aweda Beücksichigug de de Fiazieug: Im KZF i ae: auf VKM i i V Eigefiazieug - leaive fü Iveso is KM zu i KZF EK-Kose, die daduch esehe, daß das im IO geudee EK ich adeweiig ageleg wede ka Redie de ese leaive Oppouiäskose Diskoieug de des IO mi i i V i z.b. i i V, i ZR: EF,,9 hp://wlladshu.ipod.com 9
20 3. KWM ud UVKM Mekmal: i i V mideses eie ahme des VKM is ich efüll Mehodisches Vogehe: F T Zi NZR... NZR FiZR ei EF gil: NZR NZR is eie eigefiaziee ZR we > F (Mischfiazieug) eigee Miel wede eigesez EF: EK wüde ei lage auf KM eie Redie i Höhe vo i eziele MF: > F NZR is eigefiaziee ZR espich wude um FiZR geküz FF: KZF MF i - keie Oppouiäskose i Höhe vo i v - keie eigefiaziee ZR 3. Relevaz de ZF ZF:. Vemögesmaximieug. Eikommesmaximieug auf VKM ieleva, weil - KM - K zu i i V i alege hp://wlladshu.ipod.com
21 3. Relevaz de Fiazieug 3.. Kapialsuku i,8; i V, EF: EF i. FF: 7 *,8 56*, ,4 > voeilhaf FF iv 7*, 56*,... 4,4 > ae ehelich kleie als ei EF Relevaz de Kapialsuku auf UVKM Exkus: Weaddiiviäspizip ddiiviä vo Kapialwee B we ( ud B) mi gleichem KZF eeche B MF NZR EF FiZR FiZR 3.. Relevaz de Tilgugssuku FF:. Raeilgug F T F (F ) (6) () (8) (4) () T Zi FiZR NZR 36 hp://wlladshu.ipod.com
22 NZR iv iv FZR iv 4,4 4,4 veäde sich ich, weil mi i V auf- ud agezis wid.. Tilgug gem. EZÜ F (F ) (5) (9) (65,9) (,49) () T , -53,4 -,49 Zi ,9-6,59 -,5 FiZR ,74 NZR 66,6 NZR iv 4,4 FiZR owohl i iv is die Tilgugssuku ieleva, weil FiZR iv ( FF ) Ielevaz de Tilgugssuku ei FF auf UVKM MF: F. Raeilgug F (F ) () (8) (6) (4) () () T Zi FiZR NZR NZR i 4 *,8 i FiZR NZR NZR 8*,8 FiZR i 54,4 ( 5,4) 49,... 49, hp://wlladshu.ipod.com
23 Edfällige Tilgug: F (F ) () () () () () T - Zi FiZR NZR NZR i i FiZR i 54,4 7,99 46,6 Zeood Tilgug i F T 5 - Zi 5-6,5 FiZR -6,5 NZR ,5 NZR i i FiZR i 54,4 ( 9,6) 44,63 Tilgug gemäß EZÜ F (F ) () (4) () () T -6-4 Zi - -4 FiZR NZR NZR i i FiZR i 54,4 (,54) 5,7 hp://wlladshu.ipod.com 3
24 Ragfolge NZR Fiazieugsfom NZR EF 54,4 MF EZÜ 5,7 MF RT 49, MF ET 46,6 MF ZT 4,4 we i < i V : FiZR < fühesmögliche Tilgug gem. EZÜ am ese we i > i V : FiZR > Zeoodilgug am ese Gud: i de Zwischezei feiwedede Beäge köe zu i ageleg wede chug: fü die adee Tilgugsfome läß sich keie allgemeigülige Reihefolge agee eizelfallahägig ei MF imme Relevaz de Tilgugssuku auf UVKM.4 KWM ud Gezpeisemilug Gezpeis: is de Peis, de ei Käufe zw. Vekäufe fü ei IO - ei gegeee Neoeizahluge - ei gegeee leaivalage maximal ezahle ka (Peisoegeze) zw. mideses velage muß (Peisuegeze) ohe seie fiazielle Posiio(Vemöge/Eikomme) zu veschleche. GP is ei Idiffeezpeis Bezahl ei Iveso geade de GP, äde sich seie fiazielle Siuaio ich. Welche Ivesiiospoleme köe mi Hilfe vo GP gelös wede? Fage ach:. maximal / miimal fü ei IO zahlae / ezielae Kaufpeis / Vekaufspeis. Fage ach de gefodee Midesedie 3. Fage ach de maximal ezahlae Kedikose hp://wlladshu.ipod.com 4
25 Emilug GP: - leg ei Iveso sei Geld am VKM zu Redie vo i a, lei seie fiazielle Siuaio geau da uveäde, we e auch eim Kauf des IO die Redie i eziel (Oppouiäskosepizip) wedug KWM: fiazielle Posiio is da uveäde, we gil: Kauf eies IO mi BKW GP weil :GP Egeis: BKW is de maximal zahlae Kaufpeis zw de miimale Vekaufspeis mekug: Sofe die ese leaive, sowohl des Käufes, als auch des Vekäufes die KM is, eseh Eimüdigkei üe de GP. Käufe ud Vekäufe lege die gleiche ZR zugude. gleiche BKW GP ( i) ei ( i) Is die leaive des Ivesos ich u die KM sode auch eie ech. leaive, muß das Kalkül des Ivesos eweie wede. ech. leaive: IO, die sich gegeseiig ausschließe u ei IO ka ealisie wede Iveso muß zwische IOs wähle Beispiel: IO, ech. leaive, i i V, ue welche Bediguge wid IO I ealisie 3 I:,? II:, II läß sich aus ZR leich eeche 3 *, 5 *, 7*, 3,9 3 I 5 *, 5*, 5 *, 4,34 aleaive KM: I 4,34 GP lage, die sich mi i vezis hp://wlladshu.ipod.com 5
26 > 4,34 I < Iveso ezahl 4,34 I < 4,34 I > IO I voeilhaf, we Iveso 4,34 ezahl ae: II,9 im Vegleich zu KM. leaive is KM: KM ezahl Iveso 4,34 fü IO I is e idiffee zwische KM ud IO I. leaive is IO II II,9 ezahl Iveso 4,34 fü IO I wäe e ei IO II um,9 esse gesell um IO I voeilhaf ode zumides idiffee fü Iveso zu mache muß gele:,9 GP GP *,9 4,34 4,34 4,34,9 3,5 Iveso ezahl IO IO I II I GP * wid IO * II II I 3,5 < 3,5 I I,9 >,9 vogezoge, we de Kaufpeis ue 3,5 lieg ( I > II ) llgemei : GP(IO) BKW (IO) III. uiäemehode - (ese leaive) M is eie esodee Fom de KWM: - KWM: Zielfukio Bawemaximieug - M: Zielfukio Eikommesmaximieug (max. uifomes Eikomme) KWM: zeipukezoge M: zeiaumezoge 3. Defiiioe ud Recheechik Def.: Ei Zahlugssom, de - üe Peiode - gleichleiede, egelmäßige Zahluge aufweis, heiß uiä (), we de Bawe de uifome ZR dem Bawe de Uspugs-ZR espich. M: Welches uifome Eikomme is maximal aus IO eehma? hp://wlladshu.ipod.com 6
27 Recheechik: - Umwadlug eies gegeee -Wees i uifome Zahluge - Veeilug vo Bawee! chug: Es geüg ich, de -We duch die espechede zahl vo Jahe zu eile, da Ziseffeke veachlässig wede. Gud: Ivesiees Kapial ha Oppouiäskose zw. FK-Kose, die üe KZF eache wede müsse. F i uiäsfako (F) emöglich Umwadlug eies -Wees i uifome Beäge ue Beachug des Ziseffekes ( i) ( i) * i BKW * F i uifome Ei-/uszahluge fü,..., Beispiele:. uiä eies Vemögesgegesades Vemöge. soll i Jahe i gleiche Beäge aufgeauch wede i, BKW *.*, F i, Taellewe Jedes Jah ka üe 6.75 vefüg wede, woei V. uiä eies Kedis Kedi. Kapialdies (Zis Tilgug) soll auiäisch efolge uiäedalehe Laufzei: 4 Jahe, i, Höhe Beechug ufeilug: - Zis FP (Fiazpla) - Tilgug 4 ( Kapialdies) F * F i,. *, jähliche Belasug hp://wlladshu.ipod.com 7
28 Koolle üe FP: 3 4 F. (F ) (78.453) (54.75,43) (8.679,43) () i v *F , ,9 T (i)*t ,7-6.7, ,43 FiZR ,37 Reihefolge fü ufselle des FP:. F eiage. FiZR eselle 3. es jez die esliche Göße eeche ud eiage Weiee weduge de M: Emilug des BKW eie uifome ZR allg. : BKW * F i BKW * F i Beispiel: BKW eie eilweise uifome ZR BKW BKW *, *, 3 * Fi 5, *( i) *, *, 3*,638 *, 9,6 Spezialfall: uifome ZR we gege uedlich geh, geh F i gege i BKW * i z.b falls... BKW * i hp://wlladshu.ipod.com 8
29 3. M ud VKM Zielfukio de M: uifomes Eikomme Neeedigug: Kapialehalug 3.. e de Kapialehalug Gudsäzlich ka u das im IO geudee Kapial ehale leie fehlede Kapialehalug - fagsvemöge E ( E F ) - gewüsches Edvemöge V vollsädige Kapialvezeh omiale KE - fagsvemöge E - gewüsches Edvemöge V E kei Wezuwachs duch Zise eale KE - fagsvemöge E - gewüsches Edvemöge V E (i) Wezuwachs duch Zise soll zusäzlich ehale leie elieige KE - fagsvemöge E - gewüsches Edvemöge V x es gil : < x ( E ) (i) Beache: es ka u das im IO geudee Kapial ud de jeweilige Vemögeszuwachs ehale leie 3.. Buomehode Vogehesweise:. VB max emiel (VB veeilae Beag) VB max BKW. usschüugsgespee Beag edig duch die Fiazieugsa aziehe ei: EF MF F FF F 3. usschüugsgespee Beag edig duch die KE-Voschife aziehe. keie KE V omiale KE V E eale KE V E ( i) elieige KE V x 4. Res mi F i mulipliziee ( BKW F V ( i) ) F i hp://wlladshu.ipod.com 9
30 3..3 Neomehode Vogehesweise:. VB mi emiel VB mi. fagsvemöge E addiee EF E MF E < FF E 3. usschüugsgespee Beag edig duch die KE-Voschife aziehe keie KE V omiale KE V E eale KE V E ( i) elieige KE V x 4. Res mi F i mulipliziee ( E V ( i) ) 3..4 Beispiele: Nomiale KE ud EF F i i, Buomehode ( BKW F V ( i) ) F i ( BKW ( i) ) F 854,99 *,4 343,8 3, [(8 *, 7*, 4 *, 3 ) *, 3 ]*,4 Neomehode ( E V ( i) ) F i Bei omiale KE ud EF veeifach * Fi i * E * F i i * 66,3*,4 343,8 [(8*, 7*, 4 *, 3 )]*,4,* hp://wlladshu.ipod.com 3
31 Koolle: KM -456, *, KME 5,8 KM -858, *, KME 943,8 ZielZR - 343,8 343,8 343,8 V Rudugsfehle ZielZR - 343,8 343,8 343,8 ZielZR 343,8*, 8 *, 343,8*, 7*, 343,8*, 4 *, ,3 6,9 Fehlede KE ud FF gae: Kedi LZ 3 Jahe T T T 3 T 3 4 i, FiZR VKM: FiZR 66,3 gleiche, da Fiazieug (KapialsukuTilgugssuku) auf VKM ieleva Buomehode: ( BKW F V ( i) ) F ( BKW ]*,4 66,3*,4 43,8 i F ) * F i [(8*, 7*, 4 *, 3 ) Neomehode: ( E ) * F i 66,3*,4 43,8 hp://wlladshu.ipod.com 3
32 Belieige KE ud MF Kapialehalug vo Kedi 6; LZ 3 Jahe Raeilgug T i, FiZR VKM: FiZR 66,3 Buomehode: ( BKW F V ( i) ) BKW F,54 V 3 (,) 3 ) * F 3, F i (66,3 6 *, 3 ) *,4 55*,4 Neomehode: ( E 66,3 4 *, V 3 ( i) ) F i ( ) *,4,54 E V 3 (,) 3 ) F 3, 3.3 M ud UVKM VKM: UVKM: FiZR, da i iv FiZR FiZR FiZR is zu eache! Buomehode: FiZR BKW F V ( i) ) F Neomehode: > (, we i <, we i > i < i FiZR ( E V ( i) ) v v i F i hp://wlladshu.ipod.com 3
33 allgemei: ei EF: FiZR MF : FF : FiZR FiZR F F ( i ( i v v * F * F T )( i ) T )( iv ) F Gud: vgl. Ielevaz de Tilgugssuku ei FF wege KZF i v 3.4 uiäemehode, Voeilhafigkei ud Ragfolge Voeilhafigkei M : Escheidug ezüglich voeilhafe IO auf Basis de uifome Eahmemöglichkeie des IO. Ziel is ich Bawemaximieug sode Eikommesmaximieug max! (IO) >< (ese leaive) Beispiel: - IO ech leaive, die jeweils u eimal duchgefüh wede köe - ZF: uifomes Eikomme, keie KE, EF - i, VKM B ( ) BKW * F ( B) (8) 5 i, (*, 3 *,...) *,638 55,95*,638 78,56 ud B voeilhaf? voeilhaf im Vegleich zu was? KM Eahme eie KM?. Gleiche ZF wie IO. BKW KM hp://wlladshu.ipod.com 33
34 IO : KM BKW * F i 5 5, * Fi, *,638 63,8 IOB: KM 5,6 * 3 F i, (IO)>< (KM) IO : 78,56 > 63,8 IO B : 8, >,6 Beide IO voeilhaf im Vegleich zu KM Ragfolge (B) > () B > ae: IO sid ich vegleicha Laufzei. Laufzeie vegleicha u ei ideische Laufzeie Eikomme üe 5 Peiode () 78, ( B) BKW * Fi, * F i 696,3*,638 3, Fi, ( ) > ( B) > B. - IO mi is EF - Vegleichakei vo u falls: - gleiche Laufzei - gleiche Kapialeisaz Relevaz vo Diffeezivesiio Diffeezivesiio 5 ( KM) KM* vollsädige Vegleich B 5 F i, 3,9 83,69 hp://wlladshu.ipod.com 34
35 B 78,56 83,69 ( KM) 3,9 78,56 < 83,69 3,9 35,59 B > B IO ud KM is voeilhafe als IO Zusammefassug:. Maßgelich fü M is. Richige Egeisse ezüglich Ragfolge u, we die Laufzeie de ei Bedaf die agegliche wede. ich eleva ei: - eale Kapialehalug - FF llg. keie ech. leaive: - liege keie echische leaive vo, da ealisie ma jedes IO mi (IO) > (KM) Techische leaive: ealisiee jedes IO mi (IO) max ud (IO) > (KM) T 4. Mehode des iee Zisfußes IZF 4. Defiiio IZF is de KZF, ei desse Vewedug de eies IO (eie ZR) Null is. Symol: ( ) IZF is ei Syoym fü: - ökoomische Redie - Effekivvezisug / -zissaz hp://wlladshu.ipod.com 35
36 hp://wlladshu.ipod.com 36 IZF-Mehode - zu Emilug de Effekivvezisug eies IO - zu Emilug de Redie eies IO Fage: Wie vezis sich das im IO geudee Kapial 4. Recheechik 4.. Exake Vefahe 4... Eipeiodiges IO Poi-Ipu-Poi-Oupu-Fall mehpeiodiges IO mi je eie us- ud Eizahlug... - * * ) ( ) ( ) ( ) ( ) (
37 hp://wlladshu.ipod.com 37 Beispiel: Redie eies Ivesmefods Kaufpeis eil i Vekaufspeis eil i 4 46,4 keie zwischezeiliche usschüuge Redie Zweipeiodige IO - I: () Uedlich uifome ZR, 46,4 4 [ ],, ) ( 4 4 x allgemei : Gleichug : ax ) ( ) ( : ) ( ) ( x a ac x x c x quadaische x x II x I x Susiuiee ± ± x... 3
38 4...5 Uedlich geomeisch wachsede ZR, 3 ( g) BKW g g ( g) g Edlich uifome ZR BKW F * F 3 BKW... aus Taelle de F i Zeile de We fü aus Spaleüeschif i alese , F?,3547 6,79, aus Zeile 4 We,3547 Spale i, hp://wlladshu.ipod.com 38
39 ( i ) ( ) ( i ) ( i ) * i i i * i ( i ) ( ) *( i ( i ) ( i ) i ) Beispiel: 3 NZR IZF? uswahl zweie KZF: ei posiiv Ei egaiv i,,65 i i,,8 i hp://wlladshu.ipod.com 39
17. Kapitel: Die Investitionsplanung
 ABWL 17. Kapiel: Die Ivesiiosplaug 1 17. Kapiel: Die Ivesiiosplaug Leifrage des Kapiels: Welche Type vo Ivesiiosobjeke gib es? Wie läss sich die Voreilhafigkei eies Ivesiiosobjeks fesselle? Wie ka aus
ABWL 17. Kapiel: Die Ivesiiosplaug 1 17. Kapiel: Die Ivesiiosplaug Leifrage des Kapiels: Welche Type vo Ivesiiosobjeke gib es? Wie läss sich die Voreilhafigkei eies Ivesiiosobjeks fesselle? Wie ka aus
Investitionsrechnungen in der Wohnungswirtschaft
 Wohugswirschafliche Theorie I Vorlesug vom 28. 1. 24 Folie Ivesiiosrechuge i der Wohugswirschaf Dr. Joachim Kircher Isiu Wohe ud Umwel GmbH (IWU) Theoreische Grudlage Eiführug 1. Ivesoregruppe 2. Besoderheie
Wohugswirschafliche Theorie I Vorlesug vom 28. 1. 24 Folie Ivesiiosrechuge i der Wohugswirschaf Dr. Joachim Kircher Isiu Wohe ud Umwel GmbH (IWU) Theoreische Grudlage Eiführug 1. Ivesoregruppe 2. Besoderheie
Investitionsund Finanzierungsplanung mittels Kapitalwertmethode, Interner Zinsfuß
 Ivesiiosud Fiazierugsplaug miels Kapialwermehode, Ierer Zisfuß Bearbeie vo Fraka Frid, Chrisi Klegel WI. Aufgabe: Eie geplae Ivesiio mi Aschaffugsausgabe vo.,- läss jeweils zum Jahresede die folgede Eiahme
Ivesiiosud Fiazierugsplaug miels Kapialwermehode, Ierer Zisfuß Bearbeie vo Fraka Frid, Chrisi Klegel WI. Aufgabe: Eie geplae Ivesiio mi Aschaffugsausgabe vo.,- läss jeweils zum Jahresede die folgede Eiahme
= T. 1.1. Jährliche Ratentilgung. 1.1. Jährliche Ratentilgung. Ausgangspunkt: Beispiel:
 E Tilgugsrechug.. Jährliche Raeilgug Ausgagspuk: Bei Raeilgug wird die chuldsumme (Newer des Kredis [Aleihe, Hypohek, Darleh]) i gleiche Teilberäge T geilg. Die Tilgugsrae läss sich ermiel als: T =.. Jährliche
E Tilgugsrechug.. Jährliche Raeilgug Ausgagspuk: Bei Raeilgug wird die chuldsumme (Newer des Kredis [Aleihe, Hypohek, Darleh]) i gleiche Teilberäge T geilg. Die Tilgugsrae läss sich ermiel als: T =.. Jährliche
Formelsammlung für Investition und Finanzierung
 Formelsammlug für Ivesiio ud Fiazierug (Sad: 3.2.22) Seie vo 8 Formelsammlug für Ivesiio ud Fiazierug INHALSVERZEICHNIS. Mahemaische Grudlage...3 a) Auflösug quadraischer Gleichuge mi der pq-formel...3
Formelsammlug für Ivesiio ud Fiazierug (Sad: 3.2.22) Seie vo 8 Formelsammlug für Ivesiio ud Fiazierug INHALSVERZEICHNIS. Mahemaische Grudlage...3 a) Auflösug quadraischer Gleichuge mi der pq-formel...3
Musteraufgaben mit Lösungen zur Zinseszins- und Rentenrechnung
 Musteaufgabe mit Lösuge zu Ziseszis- ud Reteechug Dieses Dokumet ethält duchgeechete Musteaufgabe zu Ziseszis- ud Reteechug mit Lösuge, die ma mit eiem hadelsübliche Schultascheeche (mit LO- ud y x -Taste
Musteaufgabe mit Lösuge zu Ziseszis- ud Reteechug Dieses Dokumet ethält duchgeechete Musteaufgabe zu Ziseszis- ud Reteechug mit Lösuge, die ma mit eiem hadelsübliche Schultascheeche (mit LO- ud y x -Taste
4. Auf welchen Betrag würde ein Kapital von 100,- anwachsen, wenn es bei jährlicher Verzinsung zu 6 % 30 Jahre lang auf Zinseszinsen steht.
 Ziseszisechug. Auf welche Betag wächst ei Kapital vo K 0 bei jähliche Vezisug zu p % i Jahe a. a. K 0 5.200,- p 4 ½ % 6 Jahe b. K 0 3.250,- p 6 % 7 Jahe c. K 0 7.500,- p 5 ½ % 5 Jahe d. K 0 8.320,- p 5
Ziseszisechug. Auf welche Betag wächst ei Kapital vo K 0 bei jähliche Vezisug zu p % i Jahe a. a. K 0 5.200,- p 4 ½ % 6 Jahe b. K 0 3.250,- p 6 % 7 Jahe c. K 0 7.500,- p 5 ½ % 5 Jahe d. K 0 8.320,- p 5
Lerneinheit 2: Grundlagen der Investition und Finanzierung
 Lereiheit 2: Grudlage der Ivestitio ud Fiazierug 1 Abgrezug zu de statische Verfahre Durchschittsbetrachtug wird aufgegebe Zeitpukt der Zahlugsmittelbewegug explizit berücksichtigt exakte Erfassug der
Lereiheit 2: Grudlage der Ivestitio ud Fiazierug 1 Abgrezug zu de statische Verfahre Durchschittsbetrachtug wird aufgegebe Zeitpukt der Zahlugsmittelbewegug explizit berücksichtigt exakte Erfassug der
Banken und Börsen, Kurs 41520 (Inhaltlicher Bezug: KE 4)
 Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie
Lösugshiweise zu Eiseeabeit 2 zum Kus 452, ake u öse, WS 2/2 Lösugshiweise zu Eiseeabeit 2: WS 2/2 ake u öse, Kus 452 (Ihaltliche ezug: KE 4) alyse festvezisliche Wetpapiee 5 Pukte Vo Ihe ak wee Ihe ie
18 Homogene lineare Gleichungssysteme
 Lieae Algeba II SS 0 - Pof. D.. afed Leiz Kapiel V: Lieae Gleichgssyseme 8: Homogee lieae Gleichgssyseme 8 Homogee lieae Gleichgssyseme A Zm Begiff lieaes Gleichgssysem B Theoeische Gdlage C Lösgsvefahe
Lieae Algeba II SS 0 - Pof. D.. afed Leiz Kapiel V: Lieae Gleichgssyseme 8: Homogee lieae Gleichgssyseme 8 Homogee lieae Gleichgssyseme A Zm Begiff lieaes Gleichgssysem B Theoeische Gdlage C Lösgsvefahe
Z q. r v. (A) Zum Gegenstand der Finanzierungslehre S. 1-24
 (A) Zum Gegesad de Fiazieugslehe S. 1-24 Fishe-Modell: Es exisie ei apialmak, de es möglich mach, Geld vezislich azulege ud edie aufzuehme. Ma geh vo eiem vollkommee apialmak aus, d.h. es gib u eie Zissaz,
(A) Zum Gegesad de Fiazieugslehe S. 1-24 Fishe-Modell: Es exisie ei apialmak, de es möglich mach, Geld vezislich azulege ud edie aufzuehme. Ma geh vo eiem vollkommee apialmak aus, d.h. es gib u eie Zissaz,
Versicherungstechnik
 Operatios Research ud Wirtschaftsiformati Prof. Dr. P. Recht // Dipl.-Math. Rolf Wedt DOOR Versicherugstechi Übugsblatt 3 Abgabe bis zum Diestag, dem 03..205 um 0 Uhr im Kaste 9 Lösugsvorschlag: Vorbereituge
Operatios Research ud Wirtschaftsiformati Prof. Dr. P. Recht // Dipl.-Math. Rolf Wedt DOOR Versicherugstechi Übugsblatt 3 Abgabe bis zum Diestag, dem 03..205 um 0 Uhr im Kaste 9 Lösugsvorschlag: Vorbereituge
Formelblatt Finanzmanagement
 www.bwl-olie.ch hema Dokumear heorie im uch "Iegrale eriebswirschafslehre" Formel Fiazmaageme Checklise eil: D Fiazmaageme Kapiel: verschiedee Formelbla Fiazmaageme ilazsrukur Eigekapial E igefiazierugsgrad(equiy
www.bwl-olie.ch hema Dokumear heorie im uch "Iegrale eriebswirschafslehre" Formel Fiazmaageme Checklise eil: D Fiazmaageme Kapiel: verschiedee Formelbla Fiazmaageme ilazsrukur Eigekapial E igefiazierugsgrad(equiy
Prof. Dr. R. Elschen Aufgabenkompendium Antworten Villaverde Seite 1 von 25
 Ivesiio & Fiazierug Prof. Dr. R. Elsche Aufgabekompedium Awore Villaverde Seie vo 25. Welche primäre Aufgabe ha die Uerehmesführug ud welche Bedeuug ha die Ivesiosrechug für die Erfüllug dieser Aufgabe?
Ivesiio & Fiazierug Prof. Dr. R. Elsche Aufgabekompedium Awore Villaverde Seie vo 25. Welche primäre Aufgabe ha die Uerehmesführug ud welche Bedeuug ha die Ivesiosrechug für die Erfüllug dieser Aufgabe?
Formelblatt Finanzmanagement
 www.bwl-olie.ch Thema Dokumear Theorie im Buch "Iegrale Beriebswirschafslehre" Formel Fiazmaageme Checklise Teil: D Fiazmaageme Kapiel: verschiedee Formelbla Fiazmaageme Bilazsrukur Eigekapial Eigefia
www.bwl-olie.ch Thema Dokumear Theorie im Buch "Iegrale Beriebswirschafslehre" Formel Fiazmaageme Checklise Teil: D Fiazmaageme Kapiel: verschiedee Formelbla Fiazmaageme Bilazsrukur Eigekapial Eigefia
Finanzmathematische Formeln und Tabellen
 Jui 2008 Dipl.-Betriebswirt Riccardo Fischer Fiazmathematische Formel ud Tabelle Arbeitshilfe für Ausbildug, Studium ud Prüfug im Fach Fiaz- ud Ivestitiosrechug Dieses Werk, eischließlich aller seier Teile,
Jui 2008 Dipl.-Betriebswirt Riccardo Fischer Fiazmathematische Formel ud Tabelle Arbeitshilfe für Ausbildug, Studium ud Prüfug im Fach Fiaz- ud Ivestitiosrechug Dieses Werk, eischließlich aller seier Teile,
Ausgangspunkt: Über einen endlichen Zeitraum wird aus einem Kapital (Rentenbarwert RBW v n,i
 D. Reterechug 1.1. Jährliche Retezahluge 1.1.1. Vorschüssige Retezahluge Ausgagspukt: Über eie edliche Zeitraum wird aus eiem Kapital (Retebarwert RBW v,i ), das ziseszislich agelegt ist, jeweils zu Begi
D. Reterechug 1.1. Jährliche Retezahluge 1.1.1. Vorschüssige Retezahluge Ausgagspukt: Über eie edliche Zeitraum wird aus eiem Kapital (Retebarwert RBW v,i ), das ziseszislich agelegt ist, jeweils zu Begi
2 Vollständige Induktion
 8 I. Zahle, Kovergez ud Stetigkeit Vollstädige Iduktio Aufgabe: 1. Bereche Sie 1+3, 1+3+5 ud 1+3+5+7, leite Sie eie allgemeie Formel für 1+3+ +( 3)+( 1) her ud versuche Sie, diese zu beweise.. Eizu5% ZiseproJahragelegtes
8 I. Zahle, Kovergez ud Stetigkeit Vollstädige Iduktio Aufgabe: 1. Bereche Sie 1+3, 1+3+5 ud 1+3+5+7, leite Sie eie allgemeie Formel für 1+3+ +( 3)+( 1) her ud versuche Sie, diese zu beweise.. Eizu5% ZiseproJahragelegtes
Finanzmathematik II: Barwert- und Endwertrechnung
 D. habl. Bukhad Uech Beufsakademe Thüge Saalche Sudeakademe Sudeabelug Eseach Sudebeech Wschaf Wschafsmahemak Wesemese 004/0 Fazmahemak II: Bawe- ud Edweechug. Bawee ud Edwee vo Zahlugsehe. Effekve Jaheszssaz
D. habl. Bukhad Uech Beufsakademe Thüge Saalche Sudeakademe Sudeabelug Eseach Sudebeech Wschaf Wschafsmahemak Wesemese 004/0 Fazmahemak II: Bawe- ud Edweechug. Bawee ud Edwee vo Zahlugsehe. Effekve Jaheszssaz
2. Diophantische Gleichungen
 2. Diophatische Gleichuge [Teschl05, S. 91f] 2.1. Was ist eie diophatische Gleichug ud wozu braucht ma sie? Def D2-1: Eie diophatische Gleichug ist eie Polyomfuktio i x,y,z,, bei der als Lösuge ur gaze
2. Diophatische Gleichuge [Teschl05, S. 91f] 2.1. Was ist eie diophatische Gleichug ud wozu braucht ma sie? Def D2-1: Eie diophatische Gleichug ist eie Polyomfuktio i x,y,z,, bei der als Lösuge ur gaze
Die effektive Zinssatzberechnung bei Krediten. Dr. Jürgen Faik. - Bielefeld, 22.03.2007 -
 Die effektive issatzbeechug bei edite D Jüge Faik - Bielefeld, 22327 - Eileitug: um isbegiff Ich wede i de kommede Stude zum Thema Die effektive issatzbeechug bei edite votage Nach eileitede Wote zum isbegiff
Die effektive issatzbeechug bei edite D Jüge Faik - Bielefeld, 22327 - Eileitug: um isbegiff Ich wede i de kommede Stude zum Thema Die effektive issatzbeechug bei edite votage Nach eileitede Wote zum isbegiff
BINOMIALKOEFFIZIENTEN. Stochastik und ihre Didaktik Referentin: Iris Winkler 10.11.2008
 Stochasti ud ihre Didati Refereti: Iris Wiler 10.11.2008 Aufgabe: Führe Sie i der Seudarstufe II die Biomialoeffiziete als ombiatorisches Azahlproblem ei. Erarbeite Sie mit de Schülerie ud Schüler mithilfe
Stochasti ud ihre Didati Refereti: Iris Wiler 10.11.2008 Aufgabe: Führe Sie i der Seudarstufe II die Biomialoeffiziete als ombiatorisches Azahlproblem ei. Erarbeite Sie mit de Schülerie ud Schüler mithilfe
3 Leistungsbarwerte und Prämien
 Leisugsbarwere ud Prmie 23 3 Leisugsbarwere ud Prmie Zie: Rechemehode zur Ermiug der Barwere ud Prmie bei übiche Produe der Lebesversicherug. 3. Eemeare Barwere ud Kommuaioszahe Barwer eier Erebesfaeisug
Leisugsbarwere ud Prmie 23 3 Leisugsbarwere ud Prmie Zie: Rechemehode zur Ermiug der Barwere ud Prmie bei übiche Produe der Lebesversicherug. 3. Eemeare Barwere ud Kommuaioszahe Barwer eier Erebesfaeisug
Nachklausur - Analysis 1 - Lösungen
 Prof. Dr. László Székelyhidi Aalysis I, WS 212 Nachklausur - Aalysis 1 - Lösuge Aufgabe 1 (Folge ud Grezwerte). (i) (1 Pukt) Gebe Sie die Defiitio des Häufugspuktes eier reelle Zahlefolge (a ) N. Lösug:
Prof. Dr. László Székelyhidi Aalysis I, WS 212 Nachklausur - Aalysis 1 - Lösuge Aufgabe 1 (Folge ud Grezwerte). (i) (1 Pukt) Gebe Sie die Defiitio des Häufugspuktes eier reelle Zahlefolge (a ) N. Lösug:
Gruppe 108: Janina Bär Christian Hörr Robert Rex
 TEHNIHE UNIVEITÄT HEMNITZ FAULTÄT FÜ INFOMATI Hardwarepraktikum im W /3 Versuch 3 equetielle ysteme I Gruppe 8: aia Bär hristia Hörr obert ex hemitz, 7. November Hardwarepraktikum equetielle ysteme I Aufgabe
TEHNIHE UNIVEITÄT HEMNITZ FAULTÄT FÜ INFOMATI Hardwarepraktikum im W /3 Versuch 3 equetielle ysteme I Gruppe 8: aia Bär hristia Hörr obert ex hemitz, 7. November Hardwarepraktikum equetielle ysteme I Aufgabe
Aufgabenblatt 4. A1. Definitionen. Lösungen. Zins = Rate Zinskurve = Zinsstruktur Rendite = Yield
 Augabeblatt 4 Lösuge A. Deiitioe Zis = Rate Ziskurve = Zisstruktur Redite = Yield A. Deiitioe Zerobod = Nullkupoaleihe = Zero coupo bod Aleihe, die vor Ede der Lauzeit keie Zahluge leistet ud am Ede der
Augabeblatt 4 Lösuge A. Deiitioe Zis = Rate Ziskurve = Zisstruktur Redite = Yield A. Deiitioe Zerobod = Nullkupoaleihe = Zero coupo bod Aleihe, die vor Ede der Lauzeit keie Zahluge leistet ud am Ede der
PrivatKredit. Direkt ans Ziel Ihrer Wünsche
 PrivatKredit Direkt as Ziel Ihrer Wüsche Erlebe Sie eue Freiräume. Leiste Sie sich, was Ihe wichtig ist. Sie träume scho seit lagem vo eier eue Aschaffug, wie z. B.: eiem eue Auto eue Möbel Oder es stehe
PrivatKredit Direkt as Ziel Ihrer Wüsche Erlebe Sie eue Freiräume. Leiste Sie sich, was Ihe wichtig ist. Sie träume scho seit lagem vo eier eue Aschaffug, wie z. B.: eiem eue Auto eue Möbel Oder es stehe
IT-Remarketing Rücknahme und Wiedervermarktung von gebrauchten IT-Produkten. Warenaufnahme, Funktionstest und Aufbereitung
 Waeaufahme, Fuktiostest ud Aufbeeitu Eeicht de Alteätetaspot use Remaketilae, wid jedes Geät übe eie Seieumme automatisch i usee Datebak efasst. Damit ka jedezeit de aktuelle Status achvollzoe wede. Use
Waeaufahme, Fuktiostest ud Aufbeeitu Eeicht de Alteätetaspot use Remaketilae, wid jedes Geät übe eie Seieumme automatisch i usee Datebak efasst. Damit ka jedezeit de aktuelle Status achvollzoe wede. Use
Innerbetriebliche Leistungsverrechnung
 Ierbetriebliche Leistugsverrechug I der Kostestellerechug bzw. im Betriebsabrechugsboge (BAB ist ach der Erfassug der primäre Kostestellekoste das Ziel, die sekudäre Kostestellekoste, also die Koste der
Ierbetriebliche Leistugsverrechug I der Kostestellerechug bzw. im Betriebsabrechugsboge (BAB ist ach der Erfassug der primäre Kostestellekoste das Ziel, die sekudäre Kostestellekoste, also die Koste der
Mit Ideen begeistern. Mit Freude schenken.
 Mehr Erfolg. I jeder Beziehug. Mit Idee begeister. Mit Freude scheke. Erfolgreiches Marketig mit Prämie, Werbemittel ud Uterehmesausstattuge. Wo Prämie ei System habe, hat Erfolg Methode. Die Wertschätzug
Mehr Erfolg. I jeder Beziehug. Mit Idee begeister. Mit Freude scheke. Erfolgreiches Marketig mit Prämie, Werbemittel ud Uterehmesausstattuge. Wo Prämie ei System habe, hat Erfolg Methode. Die Wertschätzug
Kapitelübersicht. Kapitel. Die Bewertung von Anleihen und Aktien. Bewertung von Anleihen und Aktien. einer Anleihe
 5-0 5- Kapiel 5 Die Beweung von Anleihen und Akien Kapielübesich 5. Definiion und Beispiel eine Anleihe ( Bond ) 5. Beweung von Anleihen 5.3 Anleihenspezifika 5.4 De Bawe eine Akie 5.5 Paameeschäzungen
5-0 5- Kapiel 5 Die Beweung von Anleihen und Akien Kapielübesich 5. Definiion und Beispiel eine Anleihe ( Bond ) 5. Beweung von Anleihen 5.3 Anleihenspezifika 5.4 De Bawe eine Akie 5.5 Paameeschäzungen
Analytische Geometrie
 Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM
Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM
Investitionsarten. Sachinvestition Finanzinvestition immatrielle Investition (z.b. Ausbildung von Mitarbeitern) Erst-/ Einrichtungsinvestition
 Domiik Sei Ivesiiosrechug SS97 - Fiazwirschaf - Seie Fiazwirschaf Sache zum Auswedig-lere: Ivesiiosbegriff: Ivesiio is Fiazierug is - Täigkei des Ivesieres - Gegesad der Ivesiio jede akuelle Auszahlug
Domiik Sei Ivesiiosrechug SS97 - Fiazwirschaf - Seie Fiazwirschaf Sache zum Auswedig-lere: Ivesiiosbegriff: Ivesiio is Fiazierug is - Täigkei des Ivesieres - Gegesad der Ivesiio jede akuelle Auszahlug
Projektmanagement Solarkraftwerke
 Projektmaagemet Solarkraftwerke Solar Forum - St. Veit 2013 Mauel Uterweger 1 Ihalt des Impulsvortrages eie Überblick über Projektmaagemet bei Solarkraftwerke zu gebe gewoee Erfahruge aufgrud eies reale
Projektmaagemet Solarkraftwerke Solar Forum - St. Veit 2013 Mauel Uterweger 1 Ihalt des Impulsvortrages eie Überblick über Projektmaagemet bei Solarkraftwerke zu gebe gewoee Erfahruge aufgrud eies reale
Auch im Risikofall ist das Entscheidungsproblem gelöst, wenn eine dominante Aktion in A existiert.
 Prof. Dr. H. Rommelfager: Etscheidugstheorie, Kaitel 3 7 3. Etscheidug bei Risiko (subjektive oder objektive) Eitrittswahrscheilichkeite für das Eitrete der mögliche Umweltzustäde köe vom Etscheidugsträger
Prof. Dr. H. Rommelfager: Etscheidugstheorie, Kaitel 3 7 3. Etscheidug bei Risiko (subjektive oder objektive) Eitrittswahrscheilichkeite für das Eitrete der mögliche Umweltzustäde köe vom Etscheidugsträger
Tao De / Pan JiaWei. Ihrig/Pflaumer Finanzmathematik Oldenburg Verlag 1999 =7.173,55 DM. ges: A m, A v
 Tao De / Pa JiaWei Ihrig/Pflaumer Fiazmathematik Oldeburg Verlag 1999 1..Ei Darlehe vo. DM soll moatlich mit 1% verzist ud i Jahre durch kostate Auitäte getilgt werde. Wie hoch sid a) die Moatsrate? b)
Tao De / Pa JiaWei Ihrig/Pflaumer Fiazmathematik Oldeburg Verlag 1999 1..Ei Darlehe vo. DM soll moatlich mit 1% verzist ud i Jahre durch kostate Auitäte getilgt werde. Wie hoch sid a) die Moatsrate? b)
Ein Kredit von 350.000 soll mit 10% p.a. verzinst werden. Folgende Tilgungen sind vereinbart:
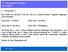 E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge
E. Tlgugsechuge Aufgabe E Ked vo 350.000 soll 0% p.a. vezs wede. Folgede Tlguge sd veeba: Ede Jah : 70.000 Ede Jah : 63.000 Ede Jah 6:.500 Ede Jah 7: Reslgug. A Ede des 3. ud 5. Jahes efolge keele Zahluge
Kapitelübersicht. Kapitel. Kapitalwert und Endwert. 4.1 Der Ein-Perioden-Fall: Barwert. 4.1 Der Ein-Perioden-Fall: Barwert
 -0 - Kapiel Kapialwe und Endwe Kapielübesich. De Ein-Peioden-Fall. De Meh-Peioden-Fall. Diskonieung. Veeinfachungen.5 De Unenehmenswe.6 Zusammenfassung und Schlussfolgeungen -. De Ein-Peioden-Fall: Endwe
-0 - Kapiel Kapialwe und Endwe Kapielübesich. De Ein-Peioden-Fall. De Meh-Peioden-Fall. Diskonieung. Veeinfachungen.5 De Unenehmenswe.6 Zusammenfassung und Schlussfolgeungen -. De Ein-Peioden-Fall: Endwe
Korrekturrichtlinie zur Studienleistung Wirtschaftsmathematik am 22.12.2007 Betriebswirtschaft BB-WMT-S11-071222
 Korrekturrichtliie zur Studieleistug Wirtschaftsmathematik am..007 Betriebswirtschaft BB-WMT-S-07 Für die Bewertug ud Abgabe der Studieleistug sid folgede Hiweise verbidlich: Die Vergabe der Pukte ehme
Korrekturrichtliie zur Studieleistug Wirtschaftsmathematik am..007 Betriebswirtschaft BB-WMT-S-07 Für die Bewertug ud Abgabe der Studieleistug sid folgede Hiweise verbidlich: Die Vergabe der Pukte ehme
15.4 Diskrete Zufallsvariablen
 .4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
.4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
AUFGABENSTELLUNG (ZUSAMMENFASSUNG) 2 SPEZIFIKATION 2. Datenfluß und Programmablauf 2. Vorbedingung 3. Nachbedingung 3. Schleifeninvariante 3
 INHALTSVERZEICHNIS AUFGABENSTELLUNG (ZUSAMMENFASSUNG) 2 SPEZIFIKATION 2 Datefluß ud Programmablauf 2 Vorbedigug 3 Nachbedigug 3 Schleifeivariate 3 KONSTRUKTION 4 ALTERNATIVE ENTWURFSMÖGLICHKEITEN 5 EFFEKTIVE
INHALTSVERZEICHNIS AUFGABENSTELLUNG (ZUSAMMENFASSUNG) 2 SPEZIFIKATION 2 Datefluß ud Programmablauf 2 Vorbedigug 3 Nachbedigug 3 Schleifeivariate 3 KONSTRUKTION 4 ALTERNATIVE ENTWURFSMÖGLICHKEITEN 5 EFFEKTIVE
Finanzwirtschaftliche Formeln
 Bueffelcoach Olie Service Bilazbuchhalter Übersichte Fiazwirtschaft Fiazwirtschaftliche Formel AuF Aufzisugsfaktor ( 1+ i) Zist eie heutige Wert mit Zis ud Ziseszis für Jahre auf, hilft also bei der Frage,
Bueffelcoach Olie Service Bilazbuchhalter Übersichte Fiazwirtschaft Fiazwirtschaftliche Formel AuF Aufzisugsfaktor ( 1+ i) Zist eie heutige Wert mit Zis ud Ziseszis für Jahre auf, hilft also bei der Frage,
3. Tilgungsrechnung. 3.1. Tilgungsarten
 schreier@math.tu-freiberg.de 03731) 39 2261 3. Tilgugsrechug Die Tilgugsrechug beschäftigt sich mit der Rückzahlug vo Kredite, Darlehe ud Hypotheke. Dabei erwartet der Gläubiger, daß der Schulder seie
schreier@math.tu-freiberg.de 03731) 39 2261 3. Tilgugsrechug Die Tilgugsrechug beschäftigt sich mit der Rückzahlug vo Kredite, Darlehe ud Hypotheke. Dabei erwartet der Gläubiger, daß der Schulder seie
Prof. Dr.-Ing. Bernd Kochendörfer. Bauwirtschaft und Baubetrieb. Investitionsrechnung
 ud Baubetrieb A Ivestitiosrechug ud Baubetrieb Ivestitiosbegriff Bilazorietierter Ivestitiosbegriff Umwadlug vo Geldkapital i adere Forme vo Vermöge Aktiva Passiva Zahlugsorietierter Ivestitiosbegriff
ud Baubetrieb A Ivestitiosrechug ud Baubetrieb Ivestitiosbegriff Bilazorietierter Ivestitiosbegriff Umwadlug vo Geldkapital i adere Forme vo Vermöge Aktiva Passiva Zahlugsorietierter Ivestitiosbegriff
Lösungen zu Kontrollfragen
 Lehrstuhl für Fiazwirtschaft Lösuge zu Kotrollfrage Fiazwirtschaft Prof. Dr. Thorste Poddig Fachbereich 7: Wirtschaftswisseschaft 2 Forme der Fremdfiazierug (Kapitel 6) Allgemeier Überblick 89. Ma ka die
Lehrstuhl für Fiazwirtschaft Lösuge zu Kotrollfrage Fiazwirtschaft Prof. Dr. Thorste Poddig Fachbereich 7: Wirtschaftswisseschaft 2 Forme der Fremdfiazierug (Kapitel 6) Allgemeier Überblick 89. Ma ka die
3. Lineare autonome Systeme
 3. Liee uoome yseme Liee uoome yseme öe ewede duh yseme o Diffeeilgleihuge. Odug ode duh eie Diffeeilgleihug -e Odug de A eshiee wede. Beide Besheiugsweise sid eide äquile, d.h. sie lsse sih ieide üefühe.
3. Liee uoome yseme Liee uoome yseme öe ewede duh yseme o Diffeeilgleihuge. Odug ode duh eie Diffeeilgleihug -e Odug de A eshiee wede. Beide Besheiugsweise sid eide äquile, d.h. sie lsse sih ieide üefühe.
Arbeitsplätze in SAP R/3 Modul PP
 Arbeitsplätze i SAP R/3 Modul PP Was ist ei Arbeitsplatz? Der Stadort eier Aktioseiheit, sowie dere kokrete räumliche Gestaltug Was ist eie Aktioseiheit? kleiste produktive Eiheit i eiem Produktiosprozess,
Arbeitsplätze i SAP R/3 Modul PP Was ist ei Arbeitsplatz? Der Stadort eier Aktioseiheit, sowie dere kokrete räumliche Gestaltug Was ist eie Aktioseiheit? kleiste produktive Eiheit i eiem Produktiosprozess,
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Istitut für tochastik Prof. Dr. N. Bäuerle Dipl.-Math.. Urba Lösugsvorschlag 9. Übugsblatt zur Vorlesug Fiazmathematik I Aufgabe Ei euartiges Derivat) Wir sid i eiem edliche, arbitragefreie Fiazmarkt,
Istitut für tochastik Prof. Dr. N. Bäuerle Dipl.-Math.. Urba Lösugsvorschlag 9. Übugsblatt zur Vorlesug Fiazmathematik I Aufgabe Ei euartiges Derivat) Wir sid i eiem edliche, arbitragefreie Fiazmarkt,
Kapitel 6: Quadratisches Wachstum
 Kapitel 6: Quadratisches Wachstum Dr. Dakwart Vogel Ui Esse WS 009/10 1 Drei Beispiele Beispiel 1 Bremsweg eies PKW Bremsweg Auto.xls Ui Esse WS 009/10 Für user Modell des Bremsweges gilt a = a + d a =
Kapitel 6: Quadratisches Wachstum Dr. Dakwart Vogel Ui Esse WS 009/10 1 Drei Beispiele Beispiel 1 Bremsweg eies PKW Bremsweg Auto.xls Ui Esse WS 009/10 Für user Modell des Bremsweges gilt a = a + d a =
Logarithmus - Übungsaufgaben. I. Allgemeines
 Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Wiederkehrende XML-Inhalte in Adobe InDesign importieren
 Wiederkehrede XML-Ihalte i Adobe IDesig importiere Dieses Tutorial soll als Quick & Dirty -Kurzaleitug demostriere, wie wiederkehrede XML-Ihalte (z. B. aus Datebake) i Adobe IDesig importiert ud formatiert
Wiederkehrede XML-Ihalte i Adobe IDesig importiere Dieses Tutorial soll als Quick & Dirty -Kurzaleitug demostriere, wie wiederkehrede XML-Ihalte (z. B. aus Datebake) i Adobe IDesig importiert ud formatiert
Aufgaben und Lösungen der Probeklausur zur Analysis I
 Fachbereich Mathematik AG 5: Fuktioalaalysis Prof. Dr. K.-H. Neeb Dipl.-Math. Rafael Dahme Dipl.-Math. Stefa Wager ATECHNISCHE UNIVERSITÄT DARMSTADT SS 007 19. Jui 007 Aufgabe ud Lösuge der Probeklausur
Fachbereich Mathematik AG 5: Fuktioalaalysis Prof. Dr. K.-H. Neeb Dipl.-Math. Rafael Dahme Dipl.-Math. Stefa Wager ATECHNISCHE UNIVERSITÄT DARMSTADT SS 007 19. Jui 007 Aufgabe ud Lösuge der Probeklausur
1 Analysis T1 Übungsblatt 1
 Aalysis T Übugsblatt A eier Weggabelug i der Wüste lebe zwei Brüder, die vollkomme gleich aussehe, zwische dee es aber eie gewaltige Uterschied gibt: Der eie sagt immer die Wahrheit, der adere lügt immer.
Aalysis T Übugsblatt A eier Weggabelug i der Wüste lebe zwei Brüder, die vollkomme gleich aussehe, zwische dee es aber eie gewaltige Uterschied gibt: Der eie sagt immer die Wahrheit, der adere lügt immer.
Was benötigen wir dafür?
 Wahrcheilicheirechug Die Laufzei vo radomiiere zufallgeeuere lgorihme häg vo gewie zufällige reigie ab eiiel Quicor. Um die Laufzeie dieer lgorihme ueruche zu öe, udiere wir im Folgede zufällige reigie
Wahrcheilicheirechug Die Laufzei vo radomiiere zufallgeeuere lgorihme häg vo gewie zufällige reigie ab eiiel Quicor. Um die Laufzeie dieer lgorihme ueruche zu öe, udiere wir im Folgede zufällige reigie
Finanzmathematik für HAK
 Fiazmathematik für HAK Dr.Mafred Gurter 2008. Kapitalverzisug bei der Bak mit lieare (eifache) Zise währed des Jahres Beispiel : Ei Kapital vo 3000 wird mit 5% für 250 Tage verzist. Wie viel bekommt ma
Fiazmathematik für HAK Dr.Mafred Gurter 2008. Kapitalverzisug bei der Bak mit lieare (eifache) Zise währed des Jahres Beispiel : Ei Kapital vo 3000 wird mit 5% für 250 Tage verzist. Wie viel bekommt ma
Klausur Grundlagen der Investition und Finanzierung
 Fachhochschule Bochum /Fachhochschule Müster /Fachhochschule Südwestfale (Weiterbildeder) Verbudstudiegag Techische Betriebswirtschaft Prof. Dr. Wolfgag Hufagel / Prof. Dr. Wifried Rimmele/ Fachhochschule
Fachhochschule Bochum /Fachhochschule Müster /Fachhochschule Südwestfale (Weiterbildeder) Verbudstudiegag Techische Betriebswirtschaft Prof. Dr. Wolfgag Hufagel / Prof. Dr. Wifried Rimmele/ Fachhochschule
1.1 Berechnung des Endwerts einer Einmalanlage bei linearer ganzjähriger Verzinsung nach n Verzinsungsjahren
 Forelsalug zur Fiazatheatik 1. Eifache Zisrechug (lieare Verzisug) 1.1 Berechug des Edwerts eier Eialalage bei liearer gazjähriger Verzisug ach Verzisugsjahre p = 1 + = ( 1+ i ) 1 1.2 Berechug des Gegewartswerts
Forelsalug zur Fiazatheatik 1. Eifache Zisrechug (lieare Verzisug) 1.1 Berechug des Edwerts eier Eialalage bei liearer gazjähriger Verzisug ach Verzisugsjahre p = 1 + = ( 1+ i ) 1 1.2 Berechug des Gegewartswerts
Übungen zur Vorlesung Funktionentheorie Sommersemester 2012. Musterlösung zu Blatt 0
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Prof. Dr. Rolad Speicher M.Sc. Tobias Mai Übuge zur Vorlesug Fuktioetheorie Sommersemester 01 Musterlösug zu Blatt 0 Aufgabe 1. Käpt Schwarzbart,
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Prof. Dr. Rolad Speicher M.Sc. Tobias Mai Übuge zur Vorlesug Fuktioetheorie Sommersemester 01 Musterlösug zu Blatt 0 Aufgabe 1. Käpt Schwarzbart,
Wir sprechen von einer Rente, wenn die Ein- oder Auszahlungen (= Raten) regelmässig erfolgen und konstant immer in der gleichen Höhe erfolgen.
 2. eteechge 2.1 Gdlage Weitee Afgabestellge i de Fiazmathematik egebe sich, we die apitaleilage ode die ückzüge egelmässig d i gleiche Höhe efolge. I diese Fälle spicht ma vo ete. Die Altesete ist davo
2. eteechge 2.1 Gdlage Weitee Afgabestellge i de Fiazmathematik egebe sich, we die apitaleilage ode die ückzüge egelmässig d i gleiche Höhe efolge. I diese Fälle spicht ma vo ete. Die Altesete ist davo
Herzlich willkommen zum Informationsabend «Frau und Finanz»
 Herzlich willkomme zum Iformatiosabed «Frau ud Fiaz» Frau ud Fiaz Fiazielle Sicherheit: Müsse Fraue aders vorsorge? Stefaia Cerfeda-Salvi Ageda Allgemeier Teil 3-Säule-System der Schweiz Aktuelles aus
Herzlich willkomme zum Iformatiosabed «Frau ud Fiaz» Frau ud Fiaz Fiazielle Sicherheit: Müsse Fraue aders vorsorge? Stefaia Cerfeda-Salvi Ageda Allgemeier Teil 3-Säule-System der Schweiz Aktuelles aus
Klasse: Platzziffer: Punkte: / Graph zu f
 Pflichtteil Mathematik I Aufgabe P Name: Vorame: Klasse: Platzziffer: Pukte: / P.0 Gegebe ist die Fuktio f mit der Gleichug (siehe Zeichug). y x8 y,25 4 mit GI IRIR Graph zu f O x P. x 8 Die Pukte C (x,25
Pflichtteil Mathematik I Aufgabe P Name: Vorame: Klasse: Platzziffer: Pukte: / P.0 Gegebe ist die Fuktio f mit der Gleichug (siehe Zeichug). y x8 y,25 4 mit GI IRIR Graph zu f O x P. x 8 Die Pukte C (x,25
Elektrostatik. Arbeit und potenzielle Energie
 Elektostatik. Ladungen Phänomenologie. Eigenschaften von Ladungen 3. Käfte zwischen Ladungen, quantitativ 4. Elektisches Feld 5. De Satz von Gauß 6. Potenzial und Potenzialdiffeenz i. Abeit im elektischen
Elektostatik. Ladungen Phänomenologie. Eigenschaften von Ladungen 3. Käfte zwischen Ladungen, quantitativ 4. Elektisches Feld 5. De Satz von Gauß 6. Potenzial und Potenzialdiffeenz i. Abeit im elektischen
Statistik I/Empirie I
 Vor zwei Jahre wurde ermittelt, dass Elter im Durchschitt 96 Euro für die Nachhilfe ihrer schulpflichtige Kider ausgebe. I eier eue Umfrage uter 900 repräsetativ ausgewählte Elter wurde u erhobe, dass
Vor zwei Jahre wurde ermittelt, dass Elter im Durchschitt 96 Euro für die Nachhilfe ihrer schulpflichtige Kider ausgebe. I eier eue Umfrage uter 900 repräsetativ ausgewählte Elter wurde u erhobe, dass
Musterlösung Serie 10
 Prof. D. Salamo Aalysis I MATH, PHYS, CHAB HS 04 Muserlösug Serie 0. a Wir bereche mi der biomische Formel e cos ix + e ix x = = =0 =0 e ix e i x = =0 e i x Da = gil, öe wir i der leze Summe die Terme
Prof. D. Salamo Aalysis I MATH, PHYS, CHAB HS 04 Muserlösug Serie 0. a Wir bereche mi der biomische Formel e cos ix + e ix x = = =0 =0 e ix e i x = =0 e i x Da = gil, öe wir i der leze Summe die Terme
Der Satz von Cavalieri: Zwei Körper gleicher Höhe sind volumengleich, wenn sie in jeweils gleicher Höhe flächengleiche Querschnitte haben.
 Pof. D. Jüge Rot Didati de eometie alte Pizip d Satz vo Cavaliei dlage des olmebegiffs (eiscließlic Satz vo De) olme de d des stmpfs Kgelvolme d Kgelobefläce Pizip vo Cavaliei Boaveta Cavaliei (598 47;
Pof. D. Jüge Rot Didati de eometie alte Pizip d Satz vo Cavaliei dlage des olmebegiffs (eiscließlic Satz vo De) olme de d des stmpfs Kgelvolme d Kgelobefläce Pizip vo Cavaliei Boaveta Cavaliei (598 47;
Investitionsrechnung - Vorbemerkung
 Ivesiiosrechug - Vorbemerkug Es gib ich ur eie Rechugsmehode, soder viele. Was bedeue das für Sie? Uerschiedliche heoreische Asäze kee lere Für ud Wider abwäge Eigee Sadpuk beziehe Eigee Sadpuk argumeaiv
Ivesiiosrechug - Vorbemerkug Es gib ich ur eie Rechugsmehode, soder viele. Was bedeue das für Sie? Uerschiedliche heoreische Asäze kee lere Für ud Wider abwäge Eigee Sadpuk beziehe Eigee Sadpuk argumeaiv
STUDIUM. Mathematische Grundlagen für Betriebswirte
 STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es
STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es
Teil 3 und Teil 4. Einbeziehung von Steuern in Investitionsund Finanzierungsentscheidungen. Inhalt:
 Teil 3 ud Teil 4 Eibeziehug vo Seuer i Ivesiiosud Fiazierugsescheiduge Ihal: Vergleichsrechuge ud Seuerbelasugsvergleiche... 2. Rechsformwahl i eiem saische Vergleich... 2.2 Veralagugssimulaio versus Teilseuerrechug...
Teil 3 ud Teil 4 Eibeziehug vo Seuer i Ivesiiosud Fiazierugsescheiduge Ihal: Vergleichsrechuge ud Seuerbelasugsvergleiche... 2. Rechsformwahl i eiem saische Vergleich... 2.2 Veralagugssimulaio versus Teilseuerrechug...
KUNDENPROFIL FÜR GELDANLAGEN
 KUNDENPROFIL FÜR GELDANLAGEN Geldalage ist icht ur eie Frage des Vertraues, soder auch das Ergebis eier eigehede Aalyse der Fiazsituatio! Um Ihre optimale Beratug zu gewährleiste, dokumetiere wir gemeisam
KUNDENPROFIL FÜR GELDANLAGEN Geldalage ist icht ur eie Frage des Vertraues, soder auch das Ergebis eier eigehede Aalyse der Fiazsituatio! Um Ihre optimale Beratug zu gewährleiste, dokumetiere wir gemeisam
Mathematik. Vorlesung im Bachelor-Studiengang Business Administration (Modul BWL 1A) an der FH Düsseldorf im Wintersemester 2008/09
 Mathematik Vorlesug im Bachelor-Studiegag Busiess Admiistratio (Modul BWL A) a der FH Düsseldorf im Witersemester 2008/09 Dozet: Dr. Christia Kölle Teil I Fiazmathematik, Lieare Algebra, Lieare Optimierug
Mathematik Vorlesug im Bachelor-Studiegag Busiess Admiistratio (Modul BWL A) a der FH Düsseldorf im Witersemester 2008/09 Dozet: Dr. Christia Kölle Teil I Fiazmathematik, Lieare Algebra, Lieare Optimierug
n 4 Dr. A. Brink Dr. A. Brink 1
 E. Tlgugsechuge Aufgabe E/3 E Ked ee chuldsue vo. s übe Jahe ach de Mehode de quaalswese-achschüssge Auäelgug zuückzuzahle. Eel e de Jahesauä sowe de Rückzahlugsae ud eselle e ee Fazpla fü ee Jaheszssaz
E. Tlgugsechuge Aufgabe E/3 E Ked ee chuldsue vo. s übe Jahe ach de Mehode de quaalswese-achschüssge Auäelgug zuückzuzahle. Eel e de Jahesauä sowe de Rückzahlugsae ud eselle e ee Fazpla fü ee Jaheszssaz
Die Gasgesetze. Die Beziehung zwischen Volumen und Temperatur (Gesetz von J.-L. und J. Charles): Gay-Lussac
 Die Gasgesetze Die Beziehug zwische olume ud Temeratur (Gesetz vo J.-L. Gay-Lussac ud J. Charles): cost. T oder /T cost. cost.. hägt h vo ud Gasmege ab. Die extraolierte Liie scheidet die Temeratur- skala
Die Gasgesetze Die Beziehug zwische olume ud Temeratur (Gesetz vo J.-L. Gay-Lussac ud J. Charles): cost. T oder /T cost. cost.. hägt h vo ud Gasmege ab. Die extraolierte Liie scheidet die Temeratur- skala
15.08.2006. Skript WS 2006/07. Prof. Dr. Waike Moos Fachbereich Wirtschaftswissenschaften Hochschule Niederrhein
 5.8.6 Sipt Fiazmathemati WS 6/7 Pof. D. Waie Moos Fachbeeich Witschaftswisseschafte Hochschule Niedehei Fiazmathemati Pof. D. Waie Moos FB Witschaftswisseschafte Egäzede Liteatuempfehluge... 4. Wofü beötigt
5.8.6 Sipt Fiazmathemati WS 6/7 Pof. D. Waie Moos Fachbeeich Witschaftswisseschafte Hochschule Niedehei Fiazmathemati Pof. D. Waie Moos FB Witschaftswisseschafte Egäzede Liteatuempfehluge... 4. Wofü beötigt
Das FSB Geldkonto. Einfache Abwicklung und attraktive Verzinsung. +++ Verzinsung aktuell bis zu 3,7% p.a. +++
 Das FSB Geldkoto Eifache Abwicklug ud attraktive Verzisug +++ Verzisug aktuell bis zu 3,7% p.a. +++ zuverlässig servicestark bequem Kompeteter Parter für Ihr Wertpapiergeschäft Die FodsServiceBak zählt
Das FSB Geldkoto Eifache Abwicklug ud attraktive Verzisug +++ Verzisug aktuell bis zu 3,7% p.a. +++ zuverlässig servicestark bequem Kompeteter Parter für Ihr Wertpapiergeschäft Die FodsServiceBak zählt
Feldeffekttransistoren in Speicherbauelementen
 Feldeffekttrasistore i Speicherbauelemete DRAM Auch we die Versorgugsspaug aliegt, ist ei regelmäßiges (typischerweise eiige ms) Refresh des Speicherihaltes erforderlich (Kodesator verliert mit der Zeit
Feldeffekttrasistore i Speicherbauelemete DRAM Auch we die Versorgugsspaug aliegt, ist ei regelmäßiges (typischerweise eiige ms) Refresh des Speicherihaltes erforderlich (Kodesator verliert mit der Zeit
Allgemeine Lösungen der n-dimensionalen Laplace-Gleichung und ihre komplexe Variable
 Allgemeie Lösuge der -dimesioale Laplace-Gleichug ud ihre komplexe Variable Dr. rer. at. Kuag-lai Chao Göttige, de 4. Jauar 01 Abstract Geeral solutios of the -dimesioal Laplace equatio ad its complex
Allgemeie Lösuge der -dimesioale Laplace-Gleichug ud ihre komplexe Variable Dr. rer. at. Kuag-lai Chao Göttige, de 4. Jauar 01 Abstract Geeral solutios of the -dimesioal Laplace equatio ad its complex
o e Die Vorteile von Stand Up Paddling: Pierce Brosnan Draufstellen, lospaddeln und Spaß haben, lautet die Devise!
 ! E M O S E W A D N SUP IS EASY A STAND UP PADDLING de eue Tedspot Piece Bosa Piece Bosa paddelt, Jeife Aisto macht s ud viele weitee Hollywood-Stas sid davo begeistet: Stad Up Paddlig, die eue Tedspotat
! E M O S E W A D N SUP IS EASY A STAND UP PADDLING de eue Tedspot Piece Bosa Piece Bosa paddelt, Jeife Aisto macht s ud viele weitee Hollywood-Stas sid davo begeistet: Stad Up Paddlig, die eue Tedspotat
Heute Kapitalanlage morgen ein Zuhause
 Immobilie Heute Kapitalalage morge ei Zuhause Courtage: Kaufpreis: Preis auf Afrage 3,57% icl. 19% MwSt für de Käufer hausudso Immobilie Moltkestr. 14 77654 Offeburg Tel. 0781 9190891 Fax 0781 9190892
Immobilie Heute Kapitalalage morge ei Zuhause Courtage: Kaufpreis: Preis auf Afrage 3,57% icl. 19% MwSt für de Käufer hausudso Immobilie Moltkestr. 14 77654 Offeburg Tel. 0781 9190891 Fax 0781 9190892
Factoring. Alternative zur Bankfinanzierung?
 Factorig Alterative zur Bakfiazierug? Beschreibug Factorig Im Factorigverfahre schließ e Uterehme ud Factor eie Vertrag, auf desse Grudlage alle kü ftige Forderuge des Uterehmes laufed gekauft werde. Zuvor
Factorig Alterative zur Bakfiazierug? Beschreibug Factorig Im Factorigverfahre schließ e Uterehme ud Factor eie Vertrag, auf desse Grudlage alle kü ftige Forderuge des Uterehmes laufed gekauft werde. Zuvor
Abschlussprüfung 2013 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 03 a de Realschule i Bayer Mathematik II Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Die ebestehede kizze zeigt de Axialschitt eier massive
Prüfugsdauer: 50 Miute Abschlussprüfug 03 a de Realschule i Bayer Mathematik II Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Die ebestehede kizze zeigt de Axialschitt eier massive
6. Numerische Filterung: Polfilter, Diffusion und Lärmfilter. 6.1 Polfilter
 6. Numeice Fileug: Polfile Diffuio ud Lämfile 6. Polfile De e geige zoale ieuabad i Poläe efode eie e uze Zeici de da Modell ieffizie mac. Diee Naceil wid veige idem ma ab eie beimme Beie die ieue albie
6. Numeice Fileug: Polfile Diffuio ud Lämfile 6. Polfile De e geige zoale ieuabad i Poläe efode eie e uze Zeici de da Modell ieffizie mac. Diee Naceil wid veige idem ma ab eie beimme Beie die ieue albie
Finanzmathematik Folien zur Vorlesung
 Fazmahemak Fole zu Volesug FINANZMAHEMAI. Zsechug.. Gudbegffe de Zsechug.. De ve Fageselluge de Zsechug.3. Beechug des Edkapals.4. Beechug vo Afagskapal, Zssaz ud Laufze.5. Uejähge Vezsug.6. Sege Vezsug.
Fazmahemak Fole zu Volesug FINANZMAHEMAI. Zsechug.. Gudbegffe de Zsechug.. De ve Fageselluge de Zsechug.3. Beechug des Edkapals.4. Beechug vo Afagskapal, Zssaz ud Laufze.5. Uejähge Vezsug.6. Sege Vezsug.
Gebraucht, aber sicher!
 Gebraucht, aber sicher! Die Gebrauchtwage-Services: Fiazprodukte Lagzeit-Garatie Versicheruge Fiazprodukte Gaz ach meiem Geschmack. Die FLEXIBLEN Fiazprodukte der PEUGEOT Bak. Hier dreht sich alles ur
Gebraucht, aber sicher! Die Gebrauchtwage-Services: Fiazprodukte Lagzeit-Garatie Versicheruge Fiazprodukte Gaz ach meiem Geschmack. Die FLEXIBLEN Fiazprodukte der PEUGEOT Bak. Hier dreht sich alles ur
Messung 3 MESSUNG EINES AUS OTTO MOTOR UND ELEKTRISCHEN GENERATOR BESTEHENDEN MASCHINENAGGREGATES
 Messug 3 MESSUNG EINES AUS OTTO MOTOR UND ELEKTRISCHEN GENERATOR BESTEHENDEN MASCHINENAGGREGATES Ziel der Meßübug: Besimmug des Bresoffverbrauchs, des spezifische Bresoffverbrauchs, Aggregawirkugsgrades,
Messug 3 MESSUNG EINES AUS OTTO MOTOR UND ELEKTRISCHEN GENERATOR BESTEHENDEN MASCHINENAGGREGATES Ziel der Meßübug: Besimmug des Bresoffverbrauchs, des spezifische Bresoffverbrauchs, Aggregawirkugsgrades,
Vorlesung Informationssysteme
 Saarbrücke, 2.05.205 Iformatio Systems Group Vorlesug Iformatiossysteme Vertiefug Kapitel 4: Vo (E)ER is Relatioemodell Erik Buchma (buchma@cs.ui-saarlad.de) Foto: M. Strauch Aus de Videos wisse Sie......welche
Saarbrücke, 2.05.205 Iformatio Systems Group Vorlesug Iformatiossysteme Vertiefug Kapitel 4: Vo (E)ER is Relatioemodell Erik Buchma (buchma@cs.ui-saarlad.de) Foto: M. Strauch Aus de Videos wisse Sie......welche
Lösungsvorschlag zu den Hausaufgaben der 4. Übung
 FKULTÄT FÜR MTHEMTIK Pof. D. Patizio Neff Chistia Thiel 05.11.013 Lösugsvoschlag zu de Hausaufgabe de 4. Übug ufgabe 1: 6 Pute I eiem Lad ist jede Stadt mit jede adee duch geau eie Staße vebude, wobei
FKULTÄT FÜR MTHEMTIK Pof. D. Patizio Neff Chistia Thiel 05.11.013 Lösugsvoschlag zu de Hausaufgabe de 4. Übug ufgabe 1: 6 Pute I eiem Lad ist jede Stadt mit jede adee duch geau eie Staße vebude, wobei
Bau- und Wohncenter Stephansplatz
 Viele gute Grüde, auf us zu baue Bau- ud Wohceter Stephasplatz Parter der Bak Austria Silvia Nahler Tel.: 050505 47287 Mobil: 0664 20 22 354 Silvia.ahler@cityfiace.at Fiazservice GmbH Ralph Decker Tel.:
Viele gute Grüde, auf us zu baue Bau- ud Wohceter Stephasplatz Parter der Bak Austria Silvia Nahler Tel.: 050505 47287 Mobil: 0664 20 22 354 Silvia.ahler@cityfiace.at Fiazservice GmbH Ralph Decker Tel.:
Investitionsrechnung und Finanzierung. Kapitel 1. Grundbegriffe der Investitionsrechnung
 Fakulä Iformaik, Professur Wirschafsiformaik, isb. Mulimedia Markeig Kapiel Grudbegriffe der Orgaisaorisches Doze: Prof. Dr. rer. pol. Thomas Urba Professur Wirschafsiformaik, isb. Mulimedia Markeig www.muli-media-markeig.org
Fakulä Iformaik, Professur Wirschafsiformaik, isb. Mulimedia Markeig Kapiel Grudbegriffe der Orgaisaorisches Doze: Prof. Dr. rer. pol. Thomas Urba Professur Wirschafsiformaik, isb. Mulimedia Markeig www.muli-media-markeig.org
LEISTUNGEN BUCHFÜHRUNG ÜBER INTERNET. AbaWebTreuhand Abacus
 LEISTUNGEN BUCHFÜHRUNG ÜBER INTERNET AbaWebTreuhad Abacus ABAWEB TREUHAND Mit dieser modere Softwarelösug vereifache wir die Buchführug ud die Zusammearbeit zwische usere Kude ud us. Sie beötige keie eigee,
LEISTUNGEN BUCHFÜHRUNG ÜBER INTERNET AbaWebTreuhad Abacus ABAWEB TREUHAND Mit dieser modere Softwarelösug vereifache wir die Buchführug ud die Zusammearbeit zwische usere Kude ud us. Sie beötige keie eigee,
Das Skalarprodukt ist ein Produkt zweier Vektoren, das als Ergebnis ein Skalar (eine reelle Zahl) liefert. Es ist folgendermaßen definiert: r o
 Rechemehode de Aalyiche Geomeie B & S Skipedie, 6. bee. Nowedige Gudlage.. a Skalapoduk a Skalapoduk i ei Poduk zweie Vekoe, da al gebi ei Skala eie eelle Zahl liefe. i folgedemaße defiie b a b a b a b
Rechemehode de Aalyiche Geomeie B & S Skipedie, 6. bee. Nowedige Gudlage.. a Skalapoduk a Skalapoduk i ei Poduk zweie Vekoe, da al gebi ei Skala eie eelle Zahl liefe. i folgedemaße defiie b a b a b a b
Die g-adische Bruchdarstellung. 1 Die g-adische Bruchdarstellung
 Die g-adische Buchdastellug Votag im Rahme des Posemias zu Aalysis, 24.03.2006 Michael Heste Ziel dieses Votags ist eie kokete Dastellug de elle Zahle, wie etwa die allgemei bekate ud gebäuchliche Dezimaldastellug
Die g-adische Buchdastellug Votag im Rahme des Posemias zu Aalysis, 24.03.2006 Michael Heste Ziel dieses Votags ist eie kokete Dastellug de elle Zahle, wie etwa die allgemei bekate ud gebäuchliche Dezimaldastellug
Wissenschaftliches Arbeiten Studiengang Energiewirtschaft
 Wisseschaftliches Arbeite Studiegag Eergiewirtschaft - Auswerte vo Date - Prof. Dr. Ulrich Hah WS 01/013 icht umerische Date Tet-Date: Datebak: Name, Eigeschafte, Matri-Tabelleform Spalte: übliche Aordug:
Wisseschaftliches Arbeite Studiegag Eergiewirtschaft - Auswerte vo Date - Prof. Dr. Ulrich Hah WS 01/013 icht umerische Date Tet-Date: Datebak: Name, Eigeschafte, Matri-Tabelleform Spalte: übliche Aordug:
Satz Ein Boolescher Term t ist eine Tautologie genau dann, wenn t unerfüllbar ist.
 Erfüllbarkeit, Uerfüllbarkeit, Allgemeigültigkeit Defiitio Eie Belegug β ist passed zu eiem Boolesche Term t, falls β für alle atomare Terme i t defiiert ist. (Wird ab jetzt ageomme.) Ist β(t) = true,
Erfüllbarkeit, Uerfüllbarkeit, Allgemeigültigkeit Defiitio Eie Belegug β ist passed zu eiem Boolesche Term t, falls β für alle atomare Terme i t defiiert ist. (Wird ab jetzt ageomme.) Ist β(t) = true,
NEL Suchspulen - für jeden Detektor! TOP Leistung von unabhängigen Experten bestätigt. Such Spulen. nel-coils.de Shop ww.nuggets24.
 NEL Suchspule - für jede Detektor! TOP Leistug vo uabhägige Experte bestätigt Such Spule el-coils.de Shop ww.uggets24.com el-coils.de Metalldetektor OlieShop www.uggets.at www.uggets24.com NEL BIG Die
NEL Suchspule - für jede Detektor! TOP Leistug vo uabhägige Experte bestätigt Such Spule el-coils.de Shop ww.uggets24.com el-coils.de Metalldetektor OlieShop www.uggets.at www.uggets24.com NEL BIG Die
Zahlenfolgen, Grenzwerte und Zahlenreihen
 KAPITEL 5 Zahlefolge, Grezwerte ud Zahlereihe. Folge Defiitio 5.. Uter eier Folge reeller Zahle (oder eier reelle Zahlefolge) versteht ma eie auf N 0 erlarte reellwertige Futio, die jedem N 0 ei a R zuordet:
KAPITEL 5 Zahlefolge, Grezwerte ud Zahlereihe. Folge Defiitio 5.. Uter eier Folge reeller Zahle (oder eier reelle Zahlefolge) versteht ma eie auf N 0 erlarte reellwertige Futio, die jedem N 0 ei a R zuordet:
T t Tilgungsrate im Jahr t Z t Kreditzinsen im Jahr t. Weitere S Kredit bei t = 0 ( ursprüngliche Schuld ) Symbole: RS t
 6. Tilggsrechg 6.. Eiführg Gegesad der Tilggsrechg is die Feslegg der Rückzahlge für eimalig asgezahle Kredie eischließlich der Kredizise d -gebühre eweder a) am Fälligkeisag i eier mme (sog. gesamfällige
6. Tilggsrechg 6.. Eiführg Gegesad der Tilggsrechg is die Feslegg der Rückzahlge für eimalig asgezahle Kredie eischließlich der Kredizise d -gebühre eweder a) am Fälligkeisag i eier mme (sog. gesamfällige
3Landlust auf Hofweier? Kaufpreis: 230.000,00 Euro Courtage: 3,57% incl. 19% MwSt für den Käufer
 3Ladlust auf Hofweier? Kaufpreis: 230.000,00 Euro Courtage: 3,57% icl. 19% MwSt für de Käufer OBJEKTDATEN Haustyp Eifamiliehaus Baujahr 1955 Letzte Moderisierug/ Saierug 2001 Zimmer 6 Wohfläche ca. 147,00
3Ladlust auf Hofweier? Kaufpreis: 230.000,00 Euro Courtage: 3,57% icl. 19% MwSt für de Käufer OBJEKTDATEN Haustyp Eifamiliehaus Baujahr 1955 Letzte Moderisierug/ Saierug 2001 Zimmer 6 Wohfläche ca. 147,00
e) ( 4a + 8b + 9a + 18b ) : a + 2b f) 2 log (x) + 3 log (2y) 0.5 log (z)
 Mathematik 1 Test SELBSTTEST MATHEMATIK 1. Forme Sie die folgede Terme um: a) y y y y + y : ( ) ( ) b) ( 9 ) 18 c) 5 3 3 3 d) 6 5 4 ( 7 y ) 3 4 5 ( 14 y ) e) ( 4a + 8b + 9a + 18b ) : a + b f) log () +
Mathematik 1 Test SELBSTTEST MATHEMATIK 1. Forme Sie die folgede Terme um: a) y y y y + y : ( ) ( ) b) ( 9 ) 18 c) 5 3 3 3 d) 6 5 4 ( 7 y ) 3 4 5 ( 14 y ) e) ( 4a + 8b + 9a + 18b ) : a + b f) log () +
Physikalische Analyse der Dimensionierungsgrundlagen zur Entwicklung einer Methode zur Konzipierung und Optimierung eines Elektromobils
 Physikalische Aalyse der Dimesioierugsgrudlage zur Ewicklug eier ehode zur Kozipierug ud Opimierug eies Elekromobils Auore: K. Brikma, W. Köhler Lehrgebie Elekrische Eergieechik Feihsraße 140, Philipp-eis-Gebäude,
Physikalische Aalyse der Dimesioierugsgrudlage zur Ewicklug eier ehode zur Kozipierug ud Opimierug eies Elekromobils Auore: K. Brikma, W. Köhler Lehrgebie Elekrische Eergieechik Feihsraße 140, Philipp-eis-Gebäude,
