Theoretische Informatik
|
|
|
- Edmund Knopp
- vor 6 Jahren
- Abrufe
Transkript
1 Theoretische Informtik Mrkus Klemm.net SS 2014 Inhltsverzeichnis 1 Automten und formle Sprchen Reguläre Sprchen Deterministische ndliche Automten (Deterministic Finite Automte, DFA) Nichtdeterministische endliche Automten (NFA) Reguläre Ausdrücke Nichtreguläre Sprchen Kontextfreie Sprchen Kellerutomten (PDAs) Kontextfreie Grmmtiken PDAs und kontextfreie Grmmtiken L-Systeme Teil Berechenrkeit und Komplexität ntscheidrkeit Komplexitätstheorie Die Klssen P und NP NP-vollständige Proleme Automten und formle Sprchen Definition in Alphet Σ ist eine endliche Menge, die nicht leer ist. Mit Σ ezeichnen wir lle lemente (Wörter), die sich durch Zusmmenfügen von Symolen us Σ ilden lssen. Die Länge eines Wortes ist die Anzhl der Symole us denen es esteht. Ds leere Wort ezeichnen wir mit ɛ. Beispiel: Alphet Σ = {,, c}, Σ = {ɛ,,, c,, c,,, c, c, c, cc,,... } 1
2 Alphet Σ = {if, then, else, x, =, 0, 1,..., 9} Wörter: if x = 0 else x = 5, if else thn x Definition ine formle Sprche, üer ein Alphet Σ ist eine Teilmenge von Σ. Beispiel: Die Menge der Schlüsselwörter der Progrmmiersprche C (if,while,else,for,... ) ist eine formle Sprche üer dem Alphet {,..., z} Die Menge der syntktisch korrekten C-Progrmme ist eine formle Sprche. Diese lässt sich drstellen üer dem Alphet {,..., z, (, ), {, }, =,!, &,,, <, >, 0,..., 9} oder üer {if,else,for,do,while,goto,==,! =, <, >, <=, >=, <<, >>, &&,, &,,, 0,..., 9} Konktention von Wörtern Definition Für Wörter v, w ist vw die Konktention. Ds Wort w n ist die n fche Konktention von w. Dei ist w 0 = ɛ. Beispiel: (c) 3 = c c c Bemerkung: s gilt ɛ Σ, d Σ die Menge ller Wörter ist. 1.1 Reguläre Sprchen Motivtion: Suche nch einem Wort s in einem Text t. Niver Algorithmus: Wort s Zeichen für Zeichen mit t vergleichen, ei Mismtch eine Stelle weiterschieen. Lufzeit: O( s t ) (schlechte Lufzeit) Deterministische ndliche Automten (Deterministic Finite Automte, DFA) in Automt ist ein formles Modell, um formle Sprchen zu verreiten. in DFA esteht us endlich vielen Zuständen und Üergängen zwischen Zuständen. In jedem Schritt verreitet der DFA ein Zeichen und wechselt dei den Zustnd. Wenn sich der DFA dei in einem ndzustnd efindet, dnn kzeptiert der DFA die Folge der ereits verreiteten Zeichen (Wort).,c,,c strt c Dieser Automt kzeptiert lle Wörter üer Σ = {,, c}, die c enthlten. Dieser Automt eschreit dmit die formle Sprche ller Wörter, die c enthlten. Zur Drstellung von DFAs verwenden wir folgende grphische Nottion: c 2
3 Zustände: Strtzustände [Hier im Script:] strt ndzustände Üergänge Weiteres Beispiel: DFA, der lle Wörter kzeptiert, die uf enden. Defnition in DFA ist ein Tupel M = (Z, Σ, δ, z 0, ) Z: Menge der Zustände Σ: ingelphet δ : Z Σ Z: Üerführungsfunktion z 0 Z: Strtzustnd Z: ndzustände Beispiel Der DFA M, der lle Wörter kzeptiert, die c enthlten, lässt sich forml eschreien durch. M = ({z 0, z 1, z 2, z }, {,, c}, δ, z 0, {z }), woei δ durch folgende Telle gegeen ist: δ z 0 z 1 z 2 z z 1 z 1 z 1 z z 0 z 2 z 0 z c z 0 z 0 z z Definition Sei M = (Z, Σ, δ, z 0, ) ein DFA. Die erweiterte Üerführungsfunktion ˆδ : Z Σ Z von M ist definiert durch: { z für w = ɛ ˆδ(z, w) = ˆδ(δ(z, ), x) für w = x mit Σ, x Σ Die von M kzeptierte Sprche ist: L(M) = {w Σ ˆδ(z 0, w) } 3
4 1.1.2 Nichtdeterministische endliche Automten (NFA) in NFA ist eine Verllgemeinerung eines DFA. Während ein DFA für jedes Pr us Zustnd und gelesenem Zeichen genu einen Folgezustnd esitzt, esitzt der NFA elieig viele Folgezustände. z ine Möglichkeit, diesen Nichtdeterminismus zu verstehen, esteht drin, einen NFA ls Modell zulässiger Zustndsfolgen zu etrchten. Beispiel: NFA, der lle Wörter kzeptiert, die c enthlten:,,c,,c z strt 0 z 1 z c 2 z So wie eine Strßenkrte mögliche Wege eschreit, eschreit uch ein NFA mögliche Zustndsfolgen ei der Verreitung eines Wortes. Inesondere weiß der NFA nicht, welchen Folgezustnd er uswählen muss. in NFA lässt sich dher nicht unmittelr ls Progrmm implementieren. Die von einem NFA M kzeptierte Sprche L(M) esteht us llen Wörtern w Σ, für die M einen ndzustnd erreichen knn. Dei müssen Knten entsprechend der Zeichen der inge durchlufen werden. Beispiel (Fortsetzung) Für die inge w = ccc knn der NFA die Zustndsfolge z 0, z 0, z 0, z 0, z 0, z 0, z 1, z 2, z, z durchlufen. D der letzte Zustnd ein ndzustnd ist, wird w kzeptiert, d.h. w L(M). Für die inge cc git es zwei Zustndsfolgen, die zu z führen (z 0, z 0, z 0, z 0, z 1, z 2, z sowie z 0, z 1, z 2, z, z, z, z ). Dher gilt cc L(M). Für die inge git es dgegen keine Zustndsfolge, mit der ein ndzustnd erreicht werden knn. Drus folgt / L(M). ine lterntive Möglichkeit, den Nichtdeterminismus eines NFA zu verstehen, esteht drin, einen NFA ls Modell zu etrchten, ds prllele Berechnungen eschreit. Die durch einen NFA eschrieenen, möglichen Zustndsüergänge lssen sich dnn durch einen Berechnungsum drstellen.: 4
5 z 0 z 0 D es eine Folge von Berechnungen git, die zu einem ndzustnd führt, wird die inge kzeptiert. Für einen NFA lässt sich die Üerführungsfunktion definieren durch δ : Z Σ P(Z) woei z δ(z, ) edeutet: Wenn der NFA sich in Zustnd z efindet und ds Zeichen erhält, dnn knn er in den Zustnd z wechseln. Ferner esitzt ein NFA einen oder mehrere Strtzustände. Beispiel strt strt NFA, der die Sprche {, } kzeptiert. Umwndlung eines NFA in einen DFA s gilt: Für jeden NFA git es einen DFA, der die gleiche Sprche erkennt. Idee zu Umwndlung: Wir vereinigen mögliche Folgezustände des NFA zu einem Zustnd des DFA. z strt 0 z 2 strt z 1 z 3 strt {z 0, z 1 } {z 2, z 3 } DFA NFA Flls es für einen Zustnd z und ein Zeichen keinen Folgezustnd git (d.h. δ(z, ) = ), führen wir einen Fehlerzustnd ein, der nicht mehr verlssen werden knn. c c strt strt,,,c 5
6 Beispiel: Umwndlung des NFA,,c,,c z strt 0 z 1 z c 2 z in einen DFA.,c z c strt 0 {z 0, z 1 } {z 0, z 2 } {z 0, z } c,,c Der Zustnd {z 0, z } ist ein ndzustnd, weil er einen ndzustnd des NFA enthält. Alle Zustände die von {z 0, z } usgehen, enthlten z und sind dmit eenflls ndzustände. Diese können vereinigt werden, ohne die vom Automten erknnte Sprche zu verändern. D die Potenzmenge P(Z) der Zustndsmenge des NFA 2 z lemente enthält, knn der us einem NFA umgewndelte DFA im schlimmsten Fll 2 z viele Zustände enthlten. s ist möglich, dss sich drunter gleichwertige Zustände efinden, die zusmmengefsst werden können. Mit dem Algorithmus Minimlutomt knn us einem DFA ein Automt erzeugt werden, der die gleiche Sprche erkennt und der miniml ezüglich der Anzhl der Zustände ist (Minimlutomt). Je zwei Minimlutomten unterscheiden sich höchstens in der Benennung der Zustände. 1.2 Reguläre Ausdrücke Definition Sei Σ ein Alphet. in regulärer Ausdruck üer Σ sowie die durch erzeugte Sprche L() sind induktiv definiert: 1. ist ein regulärer Ausdruck L( ) =. 2. Für jedes Σ {ε} ist ein regulärer Ausdruck und L() = {}. 3. Für reguläre Ausdrücke 1, 2 sind ( 1 2 ), ( 1 2 ), (1 ) reguläre Ausdrücke und L( 1 2 ) = L( 1 ) L( 2 ), L( 1 2 ) = L( 1 )L( 2 ) (dei ist L( 1 )L( 2 ) = {w 1 w 2 w 1 L( 1 ), w 2 L( 2 )}) L(1 ) = (L( 1)) Um Klmmern zu spren, legen wir folgende Regeln für die Priorität der Opertoren fest: Die höchste Priorität esitzt der Opertor, gefolgt von Konktention, gefolgt vom Opertor. 6
7 Beispiel: ( ) ist ein regulärer Ausdruck und L(( ) ) = (L( )) = (L() L()) = ({} {}) = {, }. Stz Für jeden regulären Ausdruck git es einen NFA M mit L() = L(M) Beweis: Wir induzieren üer den Aufu regulärer Ausdrücke: Induktionsnfng: Für = ist M folgender NFA: strt Für = ist M der NFA: Für = ε ist M der NFA: strt strt Induktionsschritt: Seien 1, 2 reguläre Ausdrücke und nch Induktionsvorrussetzung M 1, M 2 NFAs mit L( 1 ) = L(M 1 ), L( 2) = L(M 2 ). Ferner seien M 1, M 2 DFAs mit L(M 1 ) = L(M 1 ), L(M 2) = L(M 2 ) 1 2 : Der NFA für 1 2 ist die Vereinigung von M 1, M 2, d ein NFA mehrere Strtzustände hen drf.,, strt strt 1 2 : Skizze zur Idee: z strt 0 z z strt z 0 z z strt 0 z z z 0 z 7
8 1 z strt 0 z z ε L( 1 ) strt strt z z + = [? = ε ] Stz Für jeden NFA M git es einen regulären Ausdruck mit L() = L(M). Ohne Beweis. Beispiel:, strt Sei M der NFA in regulärer Ausdruck mit L() = L(M) ist ( ). Definition Die Menge der regulären Sprchen ist die Menge der Sprchen, die von einem DFA erknnt werden. Folgerung us den isher ufgeschrieenen Sätzen: Die NFAs erkennen genu die regulären Sprchen. Die regulären Ausdrücke erzeugen genu die regulären Sprchen. Menge der regulären Sprchen = Sprchen, die von DFAs, NFAs oder von regulären Ausdrücken erknnt werden Menge ller Sprchen Lexer in Lexer ist ein Werkzeug, ds us einem regulären Ausdruck einen DFA erzeugt, der die gleiche Sprche erkennt. Dmit können Akzeptoren für Wörter ller Muster konstruiert werden. Areitsweise eines Lexers: regulärer Ausdruck NFA DFA 8
9 1.3 Nichtreguläre Sprchen Stz Die Sprche L = { n n n 0} ist nicht regulär. Beweis: Angenommen, L sei regulär. Dnn git es einen DFA M mit L(M) = L. Nch dem Lesen von n efindet sich M in einem von Z Zuständen. D es mehr Präfixe n ls Zustände git, folgt us dem Schufchprinzip: s git zwei verschiedene Wörter n 1, n 2, so dss sich M nch dem Lesen von n 1, zw. n 2 im gleichen Zustnd z efindet. strt n 1 n 2 z n 1 D M nch Annhme n 1 n 1 kzeptiert, gelngt M von z us, durch ds Lesen von n 1, in einen ndzustnd. Dnch kzeptiert M jedoch uch ds Wort n 2 1, Widerspruch, d n 1 n Kontextfreie Sprchen Kellerutomten (PDAs) in Kellerutomt (Pushdown Automton, PDA) esitzt gegenüer einem NFA zwei zusätzliche igenschften: in Kellerutomt knn den Zustnd wechseln, ohne ein ingezeichen zu lesen (ε-üergänge) in Kellerutomt esitzt einen Stck (oder Keller ezeichnet), in dem er eine unegrenzte Anzhl von Zeichen speichern knn. Der Stck ist eine LIFO (lst in, first out) Dtenstruktur. Ferner git es nur einen Strtzustnd, ws wegen der ε-üergänge keine inschränkung ist. Grpische Drstellung von PDAs: Wir erweitern die Drstellung von NFAs um Stckopertionen. γ γ.., γ, γ z z.. Stck vorher in Üergng mit der Beschriftung, γ, γ edeutet: Stck nchher 9
10 Der PDA liest ds Zeichen der inge, entfernt ds oerste Stckzeichen γ und schreit γ uf den Stck. Jedes der Zeichen, γ, γ knn ε sein. Für = ε knn der PDA diesen Üergng usführen, ohne ein Zeichen der inge zu lesen. γ = ε knn der PDA diesen Üergng usführen, ohne ds oerste Stckzeichen zu entfernen γ = ε schreit der PDA kein Zeichen uf den Stck Dmit ein PDA einen leeren Stck erkennen knn, wird ds nde des Stcks mit dem unterstem Stckzeichen mrkiert. Zu Beginn jeder Rechnung enthält der Stck nur ds Zeichen. in PDA kzeptiert eine inge, wenn er mit dieser einen ndzustnd erreicht. Beispiel: in PDA, der die Sprche { n n n 1} kzeptiert. Für jedes gelesene wird dzu ein uf den Stck geschoen, für jedes gelesene ein vom Stck entfernt. Dnch muss der Stck leer sein., ε/, /ε, /ε ε, /ε strt z 1 z 2 z e Verhlten für die inge :
11
12 8. Verhlten für ε 12
13 Sckgsse in z 2 Verhlten für wird nicht kzeptiert, weil die inge nicht is zum nde gelesen werden knn (ein ist noch ürig) Im Folgenden erluen wir, dss ein PDA mehrere Zeichen uf den Stck schreit. Wir schreien, γ/γ 1... γ n, wenn der PDA zuerst γ n und zuletzt γ 1 uf den Stck schreit. γ 1 γ., γ, γ 1 z... γ n z. γ n. Stck vorher Stck nchher 13
14 Definition Die von einem PDA M kzeptierte Sprche L(M) ist die Menge ller w Σ, für die gilt: Der PDA M knn, usgehend vom Strtzustnd und dem initilen Stckinhlt, durch ds Lesen des Wortes w einen ndzustnd erreichen. Bemerkung: Die deterministischen PDAs (DPDAs) sind weniger leistungsfähig ls nichtdeterministische PDAs. Insesondere lssen sich PDAs nicht umwndeln in DP- DAs 1.5 Kontextfreie Grmmtiken Jede Grmmtik esitzt ein Strtsymol und rsetzungsregeln der Form linke Seite rechte Seite. Beginnend mit dem Strtsymol können diese Regeln solnge ngewendet werden, is keine Regel mehr nwendr ist. Bei einer kontextfreien Grmmtik muss die linke Seite eine Vrile sein. Beispiel: Wir etrchten eine Grmmtik, die us den Vrilen: Stz, Nominlphrse, Verlphrse, Artikel, Nomen, Ver sowie den Terminlzeichen: die, Ktze, Mus, jgdt esteht. Ds Strtsymol ist Stz, die Regeln sind Stz Nominlphrse Verlphrse Nominlphrse Artikel Nomen Ver jgt Artikel die Nomen Ktze Nomen Mus Verlphrse Ver Verlphrse Ver Nominlphrse Mögliche Aleitung: Stz Nominlphrse Verlphrse Artikel Nomen Verlphrse die Nomen Verlphrse die Ktze Verlphrse die Ktze Ver Nominlphrse die Ktze jgt Nominlphrse die Ktze jgt Artikel Nomen die Ktze jgt die Nomen die Ktze jgt die Mus Syntxum dzu: 14
15 Stz NP VP Artikel Nomen Ver NP die Ktze jgdt Artikel Nomen die Mus Definition ine kontextfreie Grmmtik ist ein Tupel G = (V, Σ, P, S), woei gilt: V ist die Menge der Vrilen oder Nonterminlzeichen Σ ist ds Alphet mit V Σ =. Die lemente us Σ heißen uch Terminlzeichen P ist die Menge der Regeln (oder Produktionen) der Form u v, woei u V, v (V Σ). S V ist ds Strtsymol Beispiel (Forts) Die Grmmtik lässt sich ls Tupel G = (V, Σ, P, S) drstellen, mit V = {Stz, Nominlphrse, Verlphrse, Ver, Artikel, Nomen}, Σ = {die,ktze,mus,jgt}, S = Stz und P wie oen. Wir schreien x y, wenn sich us x (V Σ) durch die Anwendung genu einer Regel y (V Σ) erzeugen lässt. Beispiel Definition (V Σ) ) Beispiel s gilt Stz Nominlphrse Verlphrse Artikel Nomen Verlphrse Die Reltion ist die reflexive und trnsitive Hülle der Reltion (uf s gilt Stz Stz Stz Artikel, Nomen, Verlphrse Stz die Ktze jgt die Mus 15
16 Definition Die von einer kontextfreien Grmmtik G erzeugte Sprche ist L(G) = {w Σ S w} Wenn in einer kontextfreien Grmmtik eine linke Seite durch verschiedene rechte Seiten ersetzt werden knn, verwenden wir ds Zeichen (oder), um Alterntiven nzugeen. Beispiel Die Grmmtik mit den Regeln S ε S SS S [S] können wir dmit kürzer drstellen durch S ε SS [S] Beispiel Durch die Grmmtik mit den Regeln S N S N 1S N... 9S N und dem Strtsymol S N können wir Zhlen us N 0 drstellen. Die Zhl 120 lässt sich leiten durch S N 1S N 12S N 120. Diese Regeln verwenden wir in einer weiteren Grmmtik, um rithmetische Ausdrücke zu erzeugen. Die Opertoren +,,, / sind inär, weshl vor und nch jedem Opertor ein rithmetischer Ausdruck stehen muss. Auf jede öffnende Klmmer muss eine schließende Klmmer folgen. Dmit erhlten wir die Grmmtik mit den Regeln. S S N (S ) S Op S und dem Strtsymol S. Der Ausdruck 2 (3 + 4) lässt sich leiten durch S S S S N S 2 S 2 (S ) 2 (S + S ) 2 (S N + S ) 2 (S N + S n ) 2 (3 + S N ) 2 (3 + 4) Definition ine Sprche L heißt kontextfrei, wenn es eine kontextfreie Grmmtik G git, mit L(G) = L. 16
17 1.5.1 PDAs und kontextfreie Grmmtiken Stz Kellerutomten (PDAs) kzeptieren genu die kontextfreien Sprchen. Beweis: 1. Für jeden PDA M git es eine kontextfreie Grmmtik G mit L(M) = L(G). Ohne Beweis. 2. Für jede kontextfreie Grmmtik G git es einen PDA M mit L(M) = L(G) Idee: M simuliert uf seinen Stck Aleitungen us der Grmmtik G. Wir konstruieren einen PDA M mit drei Zuständen wie folgt: Zuerst schreit M ds Strtsymol S uf den Stck und wechselt in einen weiteren Zustnd. In diesem Zustnd unterscheiden wir drei Fälle: Ds oerste Stckzeichen ist eine Vrile A. Wenn es eine Regel A γ in G git, knn M ds oerste Stckzeichen A durch γ ersetzen. ein Zeichen Σ, ds mit den nächsten Zeichen der inge üereinstimmt. Dnn wird vom Stck entfernt.. Dnn geht M in den ndzustnd üer. ε, A/γ strt ε, ε/s ε, /ε, /ε Beispiel Für die Sprche L = { n n n 0} konstruieren wir einen PDA M mit L(M) = L. L wird erzeugt von der Grmmtik mit den Regeln S S ε. Aus oigen Beweis erhlten wir den PDA. ε, S/S; ε, S/ε strt ε, ε/s ε, /ε, /ε;, /ε Verhlten für : 17
18 S S S S S Syntxnlyse Areitsweise eines Compilers if(x < 0 y < 0){... }else if... Lexer if ( ID < NUM OR ID < NUM ) {... } LS IF... Prser Syntxum Code-rzeuger Prser lssen sich in zwei Klssen unterteilen: Top-Down-Prser in Top-Down-Prser erzeugt einen Syntxum von oen nch unten. in Top-Down-Prser reitet wie ds Verfhren us dem Beweis zur Umwndlung einer kontextfreien Grmmtik in einen PDA. in Top-Down-Prser lässt sich durch rekursive 18
19 Prozeduren implementieren, von denen jede einer Regel der Grmmtik entspricht. Der Cllstck üernimmt die Funktion des Stck des PDA. Wir erluen dem Prser, die k nächsten Zeichen der inge zu sehen (lookhed von k), um dvon hängig eine Regel uszuwählen. Beim Verreiten der inge ut ein Top-Down-Prser implizit den Syntxum von oen nch unten uf. Beispiel: Prser für { n n n 0}, inge S() mtch( ) S() mtch( ) mtch( ) S() mtch( ) return true Der Cllgrph esitzt die gleiche Struktur wie der Syntxum. in Prser, der durch rekursive Funktionen einen Syntxum von oen nch unten ufut, heißt Recursive Descent Prser. Mehrdeutigkeit Definition ine Grmmtik G heißt mehrdeutig, wenn es ein w L(G) git, für ds zwei Aleitungsäume existieren. Beispiel: Die Grmmtik für rithmetische Ausdrücke mit den Regeln + / () x y z ist mehrdeutig, denn der Ausdruck x + y z esitzt zwei Aleitungsäume. + x + z y z x Auch wenn wir nur den Opertor - etrchten, ist die Grmmtik mehrdeutig, denn der Ausdruck x y z esitzt die Aleitungsäume: y 19
20 z x x y y z (x y) z x (y z) x y + z Mit oiger Grmmtik git es mehrere Proleme Sie erücksichtigt nicht die Priorität der Opertoren (Punkt vor Strich) Sie erücksichtigt nicht die Assozitivität der Opertoren Um ds Prolem der Priorität zu lösen, definieren wir eine Grmmtik, ei der sich Opertoren niedriger Priorität oen im Aleitungsum und Opertoren höherer Priorität weiter unten im Aleitungsum efinden müssen. Wir führen dzu eine Vrile T (Term) ein, us der Produkte geleitet werden können. Für die Produktionen us git es folgende Möglichkeiten: oder T + T T (1) T T + T (2) Sowohl mit (1) ls uch (2) ist gewährleistet, dss die Opertoren +, oen im Aleitungsum vorkommen. Mit (1) ist folgende Aleitung möglich. T T T entspricht (T T ) T, d.h. ist links-ssozitiv. Mit (2) ist folgende Aleitung möglich 20
21 T T T entspricht T (T T ), d.h. wäre rechtsssozitiv. Nur Grmmtik (1) erücksichtigt sowohl die Priorität ls uch die Assozitivität der Opertoren +, in korrekter Weise. ntsprechend definieren wir Regeln für T und erhlten: T + T T T T F T/F F F () x y z Diese Grmmtik ist eindeutig und erücksichtigt Priorität und Assozitivität der Opertoren. Der eindeutige Aleitungsum für x + y z ist + T T T F F F z x y Der Aleitungsum für x y z ist 21
22 T T T F F F z x y Bottom-up Prser in Buttom-up Prser ut einen Aleitungsum von unten nch oen uf. Diese lssen sich effizient relisieren durch LR-Prser. in LR-Prser liest die inge von links nch rechts und führt in jedem Schritt eine von vier möglichen Aktionen us: Shift: Ds nächste Zeichen der inge wird uf den Stck geschoen. Reduce: in oder mehrere Symole n der Spitze des Stcks entsprechen der rechten Seite γ einer Regel A γ und werden durch A ersetzt. Accept: Die inge wurde verreitet und der Stck enthält nur ds Strtsymol. rror: in Syntxfehler wird gemeldet. Um zu entscheiden, welche Aktion (Shift oder Reduce) uszuführen ist, verwendet der Prser eine Prsetelle. Beispiel Mit der eindeutigen Grmmtik von oen und der inge x + y + z führt ein LR-Prser folgende Aktionen us: 22
23 Stck ottom top Restliche inge Aktion x + y z s x +y z r F +y z r T +y z r +y z s + y z s + y z r + F z r + T z s + T z s + T z r + T F r + T r ccept Die vom Prser konstruierte Rechtsleitung lässt sich us den ersten eiden Splten von unten nch oen lesen. enso knn der Prser den Wert des Ausdrucks erechnen, wenn Zwischenwerte in den Symolen gespeichert werden. Zur Konstruktion von LR-Prsern werden Tools wie Ycc,Bison, Cup verwendet. Wenn wir die eindeutige Grmmtik für rithmetische Ausdrücke in einen Recursive Descent Prser üerführen wollen, stellen sich zwei Proleme: s ist nicht erkennr, welche Regel usgewählt werden soll Die Regel + T ist linksrekursiv. Diese führt zu einer endlosen Rekursion. Wir ruchen dher eine ndere Grmmtik. Mögliche Lösung: T + T T Dnn sind die Opertoren jedoch rechtsssozitiv, lso würde die Grmmtik flsche rgenisse erechnen. BNF (rweiterte Bckus-Nur-Form) Wir etrchten Aleitungen us : + T + T + T T + + T In BNF lässt sich dies drstellen durch T {+T } (lternt. Nottion: T (+T ) ) Dei edeutet {x}: elieig viele Vorkommen von x. Die Grmmtik für rithmetische Ausdrücke lässt sich in BNF wie folgt drstellen: T {+T T } 23
24 T F { F /F } F () Num Num Z{Z} Z Aus der Drstellung in BNF lssen sich Syntxdigrmme leiten: : F : Prolem: Aus der Drstellung in BNF oder den Syntxdigrmmen ist nicht ersichtlich, welche Assozitivität die Opertoren hen. Ohne weitere Annhmen (z.b: lle Opertoren linksssozitiv) ist diese Grmmtikeschreiung nicht eindeutig. Wir wollen nun eine eindeutige Grmmtik für Ausdrücke in Infix-Nottion konstruieren, die eindeutig und nicht linksrekursiv ist. T Til Til ε + T F T Til T Til ε T /T F () Num Num ZNum Til Num Til ε Num Z Beispiel: Aleitung des Ausdrucks
25 T Til F T Til + Num ε T Z Num Til F T Til 3 ε Num T Z Num Til F T Til 2 ε Num ε Z Num Til 4 ε L-Systeme ine Turtle esitzt eine Position in der ene und eine Orientierung. Zeichenefehle sind: forwrd(l) left(α) zw. right(α). Dreht die Turtle in 0L-System esteht, wie eine kontextfreie Grmmtik, us Vrilen, Terminlzeichen und Regeln: In jedem Aleitungsschritt müssen jedoch lle Vrilen ersetzt werden durch eine Regel. Beispiel: Koch-Kurve Vrilen: F 25
26 Terminlzeichen: +, Regeln: F F + F F + F 2 Teil Berechenrkeit und Komplexität ntscheidrkeit Ist es möglich, durch einen Algorithmus festzustellen, o ein Progrmm P eine estimmte igenschft esitzt. Progrmm P ntscheidungsverfhren j/nein igenschften können sein: Ds Progrmm P stürzt nicht Ds Progrmm P liefert immer eine Antwort Ds Progrmm P terminiert immer 1 for (k >= 3) 2 for (x,y, z := 1 to k) 3 for ( n = 3 to k) 4 if ( x^n + y^n = z^n) stop Dieses Progrmm sucht nch einen Gegeneispiel zu der von Fermt ufgestellten Behuptung (Fermts letzter Stz), dss die Gleichung x n + y n = z n keine Lösung in x, y, z N für n 3 esitzt. Dies wr üer Jhrhunderte ein ungelöstes Prolem. Offenr gilt: Ds Progrmm hält genu dnn wenn Fermts letzter Stz flsch ist. Weiteres Prolem: Ist es entscheidr o ein Progrmm P Hello World usgit? Progrmm P ntscheidungsverfhren j, git HW us/ nein Mn etrchte dzu ds Progrmm 1 void P() { 2 fermt (); 3 printf (" Hello World "); 4 } D P () genu dnn Hello World usgit, wenn fermt() terminiert, ist dieses Prolem mindestens so schwierig wie ds Hlteprolem. Um Berechenrkeit zu untersuchen, verwenden wir Progrmme uf einen strkten mit unegrenzten Speicher und Vrilen, die elieig große Werte nnehmen können, ls Berechnungsmodell. 26
27 Definition igenschft ine Sprche L heißt entscheidr, wenn es ein Progrmm P L git, mit der Für die inge w L liefert P L true Für die inge w / L liefert P L flse In Pseudocode 1 oolen P L (w) { 2 if (w L) return true ; 3 else return flse ; 4 } Üung: Zeigen Sie, dss folgende Sprchen entscheidr sind: Σ Die Sprche ller Plindrome {(M, w) M ist ein DFA mit w L(M))} {M M ist ein DFA mit L(M) = Σ }, z strt 1 z 2 δ z 1 z 2 z 2 z 2 z 1 z 2 ({z 1, z 2 }, z 1, {{z 2, z 2 }, {z 1, z 2 }}, {z 2 }) Die Srpche ist entscheidr durch ds Progrmm 1 oolen P (w) { 2 return flse ; 3 } Σ ist entscheidr durch ds Progrmm 1 oolen P Σ (w) { 2 return true ; 3 } Die Sprche ller Plindrome ist entscheidr durch 1 oolen P Plindrom (w) { 2 for ( i =1 to length ( w) /2 ) 3 if (w[i] w[ length (w) -i]) 4 return flse ; 5 return true ; 6 } 27
28 Die Sprche in {(M, w) M ist ein DFA mit w L(M))} ist entscheidr durch ds Progrmm 1 oolen P d ( DFA M,word w) { 2 return simmulte (M, w); 3 } woei simmulte(m,w) den DFA M für die inge w simuliert. Dies ist möglich (vgl. HA). {M M ist ein DFA mit L(M) = Σ } ist entscheidr durch 1 oolen P e ( DFA M ) { 2 return Minimlutomt (M) == M Σ ; 3 } strt woei M Σ der DFA HA: Ist {(M 1, M 2 ) L(M 1 ) = L(M 2 )} entscheidr Ds Hlteprolem Ds Hlteprolem ist forml die Sprche H = {(P, w) Ds Progrmm P hält für die inge w} Die Frge, o ein Progrmm P, gegeen ls Text, für eine inge w hält, ist dmit gleichwertig zu der Frge, o (P, w) H gilt. Um zu zeigen, dss H unentscheidr ist, zeigen wir zunächst: Stz Ds spezielle Hlteprolem K = {P Ds Progrmm P hält für die inge P } ist unentscheidr. Beweis: Angenommen, K ist entscheidr durch ein Progrmm P K. Drus konstruieren wir ein Progrmm P K, ds P K ls Unterprogrmm enutzt und ds in eine ndlosschleife üergeht, wenn P K true liefert hält, wenn P K flse liefert 28
29 true P P K flse P K Nch Konstruktion gilt dmit: Für die inge P hält P K genu dnn, wenn P K flse liefert. D P K nch Annhme die Sprche K entscheid, edeutet dies: Für die inge P hält PK genu dnn, wenn P nicht hält. D dies für elieige P gilt, können wir P = PK wählen. Dmit folgt: Für die inge PK hält P K genu dnn, wenn P K Widerspruch. nicht hält und dmit ein Weitere unentscheidre Proleme Mit der Untentscheidrkeit des speziellen Hlteprolems können wir die Unentscheidrkeit weiterer Proleme zeigen. Um zu zeigen, dss eine Sprche B nicht entscheidr ist, verwenden wir eine unentscheidre Sprche A. Wir zeigen, dss mit der Annhme, B sei entscheidr, ein ntscheidungsverfhren für A konstruieren lässt. Aus diesem Widerspruch folgt die Unentscheidrkeit von B. Stz H ist nicht entscheidr. Beweis: Angenommen H sei entscheidr. Dnn können wir folgendes Progrmm konstruieren, ds ds ngenommene ntescheidungsverfhren P H für H ls Unterprogrmm verwendet: 1 oolen P K ( Progrmm P ) { 2 return P H(P, P ) 3 } Dmit wäre er P K ein ntscheidungsverfhren für K, Widerspruch. Dmit folgt, dss uch die Progrmmverifiktion unentscheidr ist. 29
30 Stz Verify = {(P, S) Ds Progrmm erfüllt die Spezifiktion S} ist nicht entscheidr. Beweis: Angenommen Verify ist entscheidr durch ein Progrmm P verify. Dnn können wir ds Progrmm konstruieren. 1 oolen P H ( Progrmm P, Input w) { 2 return P verify(p, P hält für die inge w) 3 } ds dnn ein ntscheidungsverfhren für H ist, Widerspruch. Stz H ε = {P P hält für die inge ε} ist nicht entscheidr. Beweis: Sei wieder ngenommen, H ε sei entscheidr, durch ein Progrmm P Hε. 1 oolen P H ( Progrmm P, Input w){ 2 void F(){ 3 P(w) 4 } 5 return P Hε (F) 6 } Dnn ist P H er ein ntscheidungsverfhren für ds Hlteprolem, denn (P, w) H P hält für w F, hält für ε F H ε und dmit Widerspruch. Fst lle Proleme im Zusmmenhng mit Pro- Weitere unentscheidre Proleme grmmverifiktion, z.b. {P P verurscht eine Division durch 0 für eine inge } {P P verurscht einen Buffer-Overflow für eine inge } {(P 1, P 2 ) P 1 verhält sich wie P 2 } Mthemtische Proleme {F Die durch die Formel F usgedrückte Funktion ist x 0} {S S ist eine whre mthemtische Aussge } 2.2 Komplexitätstheorie Wir eschränken uns nun uf entscheidre Proleme und etrchten den Aufwnd zur Lösung dieser Proleme: 30
31 2.2.1 Die Klssen P und NP Für die O-Nottion gelten folgende Rechenregeln: O(f + g) = O(f) + O(g) O(f + g) = O(mx (f, g)) O(c f) = O(f) für eine Konstnte c > 0 O(f g) = O(f) O(g) Bei der Lufzeitmessung von Algorithmen verwenden wir ds uniforme Kostenmß, ei dem die Lufzeit ller inzelopertionen (wie Zuweisung, Vergleich, Addition) in O(1) liegt. Definition Die Komplexitätklsse P ist definiert durch P = k 1 {L L ist entscheidr durch ein Progrmm mit Lufzeit in O(n k )} woei n die Länge der inge ist. Beispiele: Folgende Sprchen liegen in P: Die Sprche ller Plindrome: Ds Progrmm 1 oolen P ( String w ) { 2 return w= reverse ( w) 3 } stellt für lle w Σ in der Zeit O( w ) fest, o w ein Plindrom ist. Dei seien reverse sowie = Funktionen mit linerer Lufzeit. Die Sprche { n n n 0}, d diese durch einen Rekursive Descent Prser in Zeit O(n) entschieden werden knn. Jede kontextfreie Sprche. s git einen Algorithmus der jede kontextfreie Sprche in Zeit O(n 3 ) entscheidet. Pfd = {(G, n 1, n 2 ) G ist ein Grph, in dem es einen Pfd von n 1 nch n 2 git }, woei G durch eine Adjzenzliste gegeen sei. Denn d die Adjzenzliste eines Grphen G = (V, ) mindestens V + lemente enthält, gilt für die Länge n der inge n V +. in ntscheidungsverfhren für Pfd ist eine in n 1 gestrtete Breitensuche mit Ziel n 2. Deren Lufzeit liegt in O( V + ). Aus V + n folgt: O( V + ) O(n). Dmit liegt die Lufzeit in des ntscheidungsverfhren in O(n), worus Pfd P folgt. 31
32 Ferner git es Sprchen, die nicht offensichtlich in P liegen. Wichtiges Beispiel: SAT = {F F ist eine erfüllre Formel der Aussgenlogik} z.b. gilt (x y) z SAT, x x / SAT Um für eine Formel F zu prüfen, o F SAT gilt, können wir lle 2 n Belegungen erzeugen und jeweils den Whrheitswert erechnen (n sei die Anzhl der Vrilen in F ). Die Lufzeit dieses ntscheidungsverfhren liegt in O(2 n f(n)), woei f(n) die Zeit ist, um den Whrheitswert zu erechnen. Wir können jedoch in polynomieller Zeit verifizieren, dss F SAT gilt, wenn eine erfüllende Belegung c F für F eknnt ist. Denn dzu muss ds ntscheidungsverfhren lediglich den Whrheitswert von F unter der Belegung c F erechnen, ws in der Zeit O( F ) möglich ist. Definition Die Komplexitätsklsse NP ist definiert durch NP = k 1 {L L ist verifizierr in Zeit O(n k )} woei n die Länge der inge ist. Beispiel: s gilt SAT NP, d mit einer erfüllenden Belegung für F in Zeit O( F ) verifiziert werden knn, o F SAT gilt. s gilt P NP, denn für jede Sprche L P git es ein ntscheidungsverfhren mit einer Lufzeit in O(n k ). Dies ist eenflls ein Verifizierungsverfhren ds kein Zertifikt verwendet. Uneknnt ist, o P = NP gilt. Die Klsse P wird etrchtet ls Klsse der effizient lösren Proleme. Gründe dzu: Die meisten Proleme in P lssen sich in Zeit O(n k ) mit einem kleinen k lösen. Diese Proleme sind dmit uch prktisch lösr NP-vollständige Proleme Die NP-vollständigen Proleme sind eine Klsse von Prolemen in NP, für die keine effizienten ntscheidungsverfhren eknnt sind. Alle eknnten Verfhren esitzen exponentielle Lufzeit. Die NP-vollständigen Proleme sind mindestens so schwierig wie jedes ndere Prolem in NP. s gilt: Wenn ein effizientes ntscheidungsverfhren für ein NP-vollständiges Prolem gefunden wird, dnn ist für jedes Prolem in NP ein effizientes ntscheidungsverfhren eknnt. Genuer: 32
33 Stz s gilt P = NP genu dnn, wenn es ein NP-vollständiges Prolem L mit L P git. Mn vermutet, dss P NP gilt, weil isher kein NP-vollständiges Prolem in P gefunden wurde. Sitution für P NP: P NP-v. NP ntscheidre Proleme Alle Sprchen Stz Ds rfüllrkeitsprolem der Aussgenlogik SAT = {F F ist eine erfüllre Formel der Aussgenlogik} ist NP-vollständig. Bemerkung: Ds schnellste eknnte Verfhren für SAT ht die Lufzeit O(1, 308 n p(n)), woei p ein Polynom ist. Anwendungen: Autokonfigurtion: Die estellren Konfigurtionen knn mn durch Regeln in Form von ussgenlogischen Formelen eschreien, z.b: Sportfhrwerk Leichtm (Motor 2.0 Motor 2.5 Motor 3.0) Alle derrtigen Formel werden mit verknüpft zu einer Formel F 1. Die Wünsche des Kunden lssen sich ls Formel F 2 eschreien. Die Kundenwünsche sind erfüllr, wenn F 1 F 2 erfüllr ist. 33
34 Vereinfchen von Schltkreisen Angenommen, es ist ein Referenzentwurf für einen Schltkreis vorhnden. Dieser ntwurf soll nun vereinfcht werden (weniger Gtter), um die Herstellungskosten zu senken. Um zu prüfen, o dieser Schltkreis gleichwertig zum Referenzentwurf ist, wird der Referenzentwurf durch eine Formel F R der Aussgenlogik, der vereinfchte Schltkreis durch eine Formel F S. Dnn muss F R F S eine Tutologie sein. Dies ist gleichwertig dmit, dss (F R F S ) unerfüllr ist. D.h., eide Schltkreise sind gleichwertig genu dnn, wenn (F R F S ) / SAT. Stz Ds Prolem Hmilton-Kreis = {G Der Grph G esitzt einen Hmiltonkreis } ist NP-vollständig. Verllgemeinerung dvon: Trveling Slesmn Prolem (TSP). Gegeen n Städte und Verindungen zwischen diesen Städten, gesucht ist eine kürzeste Rundreise durch lle Städte. Stz Ds Prolem T SP = {(M, k) M ist eine ntfernungsmtrix und es git eine Rundreise der Länge k} ist NP-vollständig. Bemerkung: Ds Prolem, eine kürzeste Rundreise zu erechnen, ist mindestens so schwierig wie oiges ntscheidungsprolem. Anwendungen: Pltine ohren: Um die Bohrzeit für eine Pltine zu minimieren, muss ein TSPfür die Bohrlöcher gelöst werden. Auf einer Fertigungsstrße sollen Produkte P 1,..., P n hergestellt werden. Dzu muss die Fertigungsstrße jeweils umgerüstet werden. Sei d ij der Zeitufwnd, um eine Fertigungsstrße die Produkt i herstellt, für Produkt j umzurüsten. Um eine Reihenfolge festzulegen, die die Summe der Rüstzeiten minimiert, muss ein TSP für die Mtrix (d ij ) gelöst werden Weiteres, ähnliches Prolem: Kürzester Hmiltonpfd Dieses Prolem ist eenflls NP-vollständig. Anwendung DNA-Sequenzierung ine DNA-Sequenz ist ein Wort üer dem Alphet {A, C, G, T }. Um eine DNA zu sequenzieren, wird diese in kleine Bruchstücke geschnitten, diese sequenziert, und us diesen Bruchstücken die ursprüngliche Sequenz rekonstruiert. Anstz dzu: Kürzeste gemeinsme Oersequenz (Shortest Common Supersequence) estimmen, d.h. eine kürzeste Sequenz finden, die lle Bruchstücke ls Teilwort enthält. Dzu wird nhnd der Üerlppung zweier Bruchstücke ein Astnd erechnet und dmit ein Short Common Superstring zw. kürzester Hmiltonpfd-Pfd-Prolem gelöst. 34
35 Beispiel Ursprüngliche Sequenz: AT GCAA Bruchstücke: AT G, CAA, GCA, T GC Algorithmen für TSP: Nerest Neighor Greedy Algorithmus: Strte in einem elieigen Knoten Solnge noch nicht lle Knoten esucht wurden: Wähle einen nächsten unesuchten Nchrn des ktuellen Knoten us und verlängere den ktuellen Pfd Greedy-Algorithmen wählen in jeden Schritt eine lokl optimle Teillösung us. Greedy-Algorithmen können optiml sein. Für ds TSP ist der Greedy-Algorithmus nicht optiml, er knn elieig schlechte Lösungen liefern. s git einen Algorithmus, der eine optimle Lösung liefert, mit Lufzeit in O(n 2 2 n ), woei n = V. Approximtion: Wir versuchen, einen Rundweg zu finden, dessen Länge etw so groß ist, wie die kürzeste Länge. Ds metrische TSP ist ein TSP, ei dem der Astnd d ij zweier Knoten eine Metrik ist. Für ds metrische TSP git es einen Approximtionslgorithmus mit Lufzeit in O(n 2 log n), der eine Lösung liefert, die eine Länge 2 optimle Länge esitzt. Ds Rucksckprolem in Rucksck der Größe S > 0 soll mit einer Auswhl von Gegenständen 1,..., n der Größe s 1,..., s n > 0 mximl epckt werden. Gesucht ist lso eine Menge C {1,..., n} mit s k S und Anwendungen: CD mit mp3 optiml efüllen Budget mximl verruchen k C s k mximl k C Ds Rucksckprolem ist NP-vollständig. Algorithmus für Rücksck: Sei r(k, s) die mximle Füllmenge eines Rucksckes der Größe s, 0 s S, der mit einer Auswhl von Gegenständen 1,..., k epckt ist. Gesucht ist r(n, S). Wir erechnen r(k, s) für 1 k n, 0 s S mit Hilfe einer Feststellung: Wenn für lle 0 l s, r(k 1, l) ereits eknnt ist, lässt sich drus r(k, s) erechnen: Wenn der Gegenstnd k nicht eingepckt wird, gilt r(k, s) = (k 1, s) 35
36 Wenn der Gegenstnd k eingepckt wird, gilt r(k, s) = r(k 1, s s k ) + s k Drus ergit sich 0 für k = 0 r(k, s) = r(k 1, s) für s < s k mx (r(k 1, s), r(k 1, s s k ) + s k ) sonst Lufzeit: O(nS). Dies ist kein Widerspruch dzu, dss Rucksck NP-vollständig ist, denn die Länge der inge ist log 2 S + n log 2 s k S = 2 log 2 S k=1 36
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Teil V: Formale Sprachen
 Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Inhaltsverzeichnis. Inhaltsverzeichnis... 1 3.Logik... 2. 3.1 Zahlensysteme... 2. 3.2 Grundbegriffe zweiwertiger Logik... 13
 Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Identifizierbarkeit von Sprachen
 FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
Karlsruher Institut für Technologie
 Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Seminar Quantum Computation - Finite Quanten-Automaten und Quanten-Turingmaschinen
 Seminr Quntum Computtion - Finite Qunten-Automten und Qunten-Turingmschinen Sebstin Scholz sscholz@informtik.tu-cottbus.de Dezember 3. Einleitung Aus der klssischen Berechenbrkeitstheorie sind die odelle
Seminr Quntum Computtion - Finite Qunten-Automten und Qunten-Turingmschinen Sebstin Scholz sscholz@informtik.tu-cottbus.de Dezember 3. Einleitung Aus der klssischen Berechenbrkeitstheorie sind die odelle
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
Public-Key-Verfahren: Diffie-Hellmann und ElGamal
 Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Endliche Automaten. S. Kuske: Endliche Automaten; 6.Novenber 2006
 1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
Einführung in die Schaltalgebra
 Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Erweitern. a b. bd + bc. bd = ad+bc. bei ganzzahligem Nenner: Hauptnenner (= kgv der Nenner), z.b. 4 6 + 3 4 = 8 12 + 9. a d = ac
 F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit bietet, ihre statistischen Meldungen über das Internet auszufüllen und einzureichen.
 Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
 S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
Definition Suffixbaum
 Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
. Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
Programmieren in C/C++ und Matlab
 Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Motivation. Kap. 4.2 Binäre Suchbäume ff Kap. 4.3: AVL-Bäume. Überblick. Pseudocode von SEARCH. in binären Suchbäumen. in binären Suchbäumen
 Kp. 4.2 inäre Schäme ff Kp. 4.: VL-äme Professor r. Lehrsthl für lgorithm Engineering, LS11 Fkltät für Informtik, TU ortmnd Motition Wrm soll ich hete hier leien? lncierte äme rchen Sie immer wieder! Ws
Kp. 4.2 inäre Schäme ff Kp. 4.: VL-äme Professor r. Lehrsthl für lgorithm Engineering, LS11 Fkltät für Informtik, TU ortmnd Motition Wrm soll ich hete hier leien? lncierte äme rchen Sie immer wieder! Ws
Shortest Path Algorithmus von Edsger Dijkstra
 Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Einschub: Zahlendarstellung und Codes
 Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
Endliche Automaten. Prof. Dr. W. Vogler. Sommersemester 2007
 Endliche Automten Prof. Dr. W. Vogler Sommersemester 2007 1 INHALTSVERZEICHNIS i Inhltsverzeichnis 1 Wörter und Monoide 1 2 Endliche Automten 4 3 Anwendung: Diophntische Gleichungen 9 4 Minimierung endlicher
Endliche Automten Prof. Dr. W. Vogler Sommersemester 2007 1 INHALTSVERZEICHNIS i Inhltsverzeichnis 1 Wörter und Monoide 1 2 Endliche Automten 4 3 Anwendung: Diophntische Gleichungen 9 4 Minimierung endlicher
Reguläre Sprachen und endliche Automaten
 2 Reguläre Sprchen und endliche Automten Sei Σ = {, b,...} ein endliches Alphbet. Ein endliches Wort über Σ ist eine Folge w = 0... n 1, wobei i Σ für i = 0,...,n 1. Wir schreiben w für die Länge von w,
2 Reguläre Sprchen und endliche Automten Sei Σ = {, b,...} ein endliches Alphbet. Ein endliches Wort über Σ ist eine Folge w = 0... n 1, wobei i Σ für i = 0,...,n 1. Wir schreiben w für die Länge von w,
5.4 CMOS Schaltungen und VLSIDesign
 Kp5.fm Seite 447 Dienstg, 7. Septemer 2 :55 3 5.4 CMOS Schltungen und VLSI Design 447 r u u r id + + A. 5.39: Progrmmierrer Gitterustein 5.4 CMOS Schltungen und VLSIDesign Die Boolesche Alger eginnt mit
Kp5.fm Seite 447 Dienstg, 7. Septemer 2 :55 3 5.4 CMOS Schltungen und VLSI Design 447 r u u r id + + A. 5.39: Progrmmierrer Gitterustein 5.4 CMOS Schltungen und VLSIDesign Die Boolesche Alger eginnt mit
Seminar zum anorganisch-chemischen Praktikum. Quantitative Analyse. Patrick Schwarz
 Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
 Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Boole'sche Algebra. Inhaltsübersicht. Binäre Funktionen, Boole'sche Algebren, Schaltalgebra. Verknüpfungen der mathematischen Logik
 Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
über der Strangbreite 2. Zugleich vermindert Einschlüssen, wodurch sich die Qualität des gegossenen Stahls verbessert.
 S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
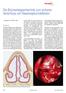 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Installations und Bedienungsanleitung
 Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Logische Grundschaltungen
 Elektrotechnisches Grundlgen-Lor II Logische Grundschltungen Versuch Nr. 9 Erforderliche Geräte Anzhl Bezeichnung, Dten GL-Nr. 1 Voltmeter 335 1 Steckrett SB 1 1 Steckrett SB 2 mit 5V Netzteil 1 Steckrett
Elektrotechnisches Grundlgen-Lor II Logische Grundschltungen Versuch Nr. 9 Erforderliche Geräte Anzhl Bezeichnung, Dten GL-Nr. 1 Voltmeter 335 1 Steckrett SB 1 1 Steckrett SB 2 mit 5V Netzteil 1 Steckrett
Nutzung der Abwärme aus Erneuerbare-Energie-Anlagen
 5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
Was bisher geschah: Formale Sprachen
 Was isher geschah: Formale Sprachen Alphaet, Wort, Sprache Operationen und Relationen auf Wörtern und Sprachen reguläre Ausdrücke: Syntax, Semantik, Äquivalenz Wortersetzungssysteme Wortersetzungsregeln
Was isher geschah: Formale Sprachen Alphaet, Wort, Sprache Operationen und Relationen auf Wörtern und Sprachen reguläre Ausdrücke: Syntax, Semantik, Äquivalenz Wortersetzungssysteme Wortersetzungsregeln
c dl SPiC (Teil C, SS 11) 13 Zeiger und Felder 13.1 Zeiger Einführung 13 1 Zeigervariable := Behälter für Verweise ( Adresse) Beispiel int x = 5;
 Überblick: Teil C Systemnhe Softwreentwicklung Einordnung: Zeiger (Pointer) Literl: Drstellung eines Wertes 0110 0001 12 Progrmmstruktur und Module Vrible: Bezeichnung chr ; eines Dtenobjekts Behälter
Überblick: Teil C Systemnhe Softwreentwicklung Einordnung: Zeiger (Pointer) Literl: Drstellung eines Wertes 0110 0001 12 Progrmmstruktur und Module Vrible: Bezeichnung chr ; eines Dtenobjekts Behälter
Wie erfahre ich, welches Programm ich verwenden muss? 1. Wie kann ich meine Videobänder auf eine Disc übertragen? 5
 hp dvd writer Wie... Inhlt Wie erfhre ich, welches Progrmm ich verwenden muss? 1 Deutsch Wie knn ich eine Disc kopieren? 2 Wie knn ich meine änder uf eine Disc üertrgen? 5 Wie knn ich einen DVD-Film erstellen?
hp dvd writer Wie... Inhlt Wie erfhre ich, welches Progrmm ich verwenden muss? 1 Deutsch Wie knn ich eine Disc kopieren? 2 Wie knn ich meine änder uf eine Disc üertrgen? 5 Wie knn ich einen DVD-Film erstellen?
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Personal und Finanzen der öffentlich bestimmten Fonds, Einrichtungen, Betriebe und Unternehmen (FEU) in privater Rechtsform im Jahr 2003
 Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
5.3 Dynamisches Sitzen und Stehen
 Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
17 Doppelbündel-Rekonstruktion mit Semitendinosussehne
 Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Dental-CT bei Kindern Technische Vorgehensweise und exemplarische Befunde
 Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil I: Theorie. Michael Buhlmann
 Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Kapitel 8 Apps installieren und verwalten
 Kpitel 8 Apps instllieren und verwlten In diesem Kpitel sehen wir uns die Stndrdquelle ller Apps einml etws genuer n, den Google Ply Store (kurz: Google Ply oder Ply Store). Er ist der Dreh- und Angelpunkt,
Kpitel 8 Apps instllieren und verwlten In diesem Kpitel sehen wir uns die Stndrdquelle ller Apps einml etws genuer n, den Google Ply Store (kurz: Google Ply oder Ply Store). Er ist der Dreh- und Angelpunkt,
Digitaltechnik. 3 Sequenzielle. Schaltungen. Revision 1.1
 igitltechnik 3 Sequenzielle Schltungen A Revision 1.1 Trnsitionssysteme Synchroner sequenzieller Entwurf Timing-Anlyse Pipelining Mely und Moore Mschinen Zustndsmschinen in Verilog Sequentielle Schltungen
igitltechnik 3 Sequenzielle Schltungen A Revision 1.1 Trnsitionssysteme Synchroner sequenzieller Entwurf Timing-Anlyse Pipelining Mely und Moore Mschinen Zustndsmschinen in Verilog Sequentielle Schltungen
In Fachwerken gibt es demnach nur konstante Normalkräfte. Die Fachwerksknoten sind zentrale Kraftsysteme.
 Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
7. Portfolioinvestitionen und Wechselkursschwankungen. Literatur. Prof. Dr. Johann Graf Lambsdorff Universität Passau SS 2008
 Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
www. line21 Kommunikation Daten- und Telefontechnik über 1 Kabel mit 4 Adern. Kein Problem mit line21 natürlich von Rutenbeck!
 Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Version 3. Installation. Konfiguration. Bedienung. Referenz. SYNCING.NET Technologies GmbH Weipertstr. 8-10 74076 Heilbronn www.syncing.
 Rev. 03 SNT 000.2547 Version 3 Instlltion Konfigurtion Bedienung Referenz SYNCING.NET Technologies GmbH Weipertstr. 8-10 74076 Heilbronn www.syncing.net Inhltsverzeichnis Inhltsverzeichnis Einleitung 5
Rev. 03 SNT 000.2547 Version 3 Instlltion Konfigurtion Bedienung Referenz SYNCING.NET Technologies GmbH Weipertstr. 8-10 74076 Heilbronn www.syncing.net Inhltsverzeichnis Inhltsverzeichnis Einleitung 5
Prozeßalgebren. Prof. Dr. Ursula Goltz
 Prozeßlgebren Prof Dr Ursul Goltz Stnd: 24 Oktober 2012 Vorwort Ds vorliegende Skript ist die Ausrbeitung einer Vorlesung, die wesentliche Grundbegriffe us dem weiten Feld der Prozeßlgebren einführt Dbei
Prozeßlgebren Prof Dr Ursul Goltz Stnd: 24 Oktober 2012 Vorwort Ds vorliegende Skript ist die Ausrbeitung einer Vorlesung, die wesentliche Grundbegriffe us dem weiten Feld der Prozeßlgebren einführt Dbei
Einführung: Sequence Alignment
 lgorthmsche nendungen - Prktkum WS 7/8 ynmsche Progrmmerung / reedy-lgorthmen ufgen 8 - Hener Klocke Fchhochschule Köln Informtk Prktkum: ynmsche Progrmmerung / reedy-lgorthmen ufgen 8 9 ufge Kptel ynmsche
lgorthmsche nendungen - Prktkum WS 7/8 ynmsche Progrmmerung / reedy-lgorthmen ufgen 8 - Hener Klocke Fchhochschule Köln Informtk Prktkum: ynmsche Progrmmerung / reedy-lgorthmen ufgen 8 9 ufge Kptel ynmsche
Frustration ist ein alltägliches Phänomen, und
 FESTKÖRPERPHYSIK Topologische Spinflüssigkeiten Frustrtion mgnetischer Momente durch widerstreitende Kopplungen knn zu Spinflüssigkeiten mit topologischer Ordnung führen. Ki Phillip Schmidt und Simon Trest
FESTKÖRPERPHYSIK Topologische Spinflüssigkeiten Frustrtion mgnetischer Momente durch widerstreitende Kopplungen knn zu Spinflüssigkeiten mit topologischer Ordnung führen. Ki Phillip Schmidt und Simon Trest
Gerd Wöstenkühler. Grundlagen der Digitaltechnik Elementare Komponenten, Funktionen und Steuerungen
 Gerd Wöstenkühler Grundlgen der Digitltehnik Elementre Komponenten, Funktionen und Steuerungen Inhlt 1 Einleitung... 11 1.1 Anloge unddigitledrstellungsformen... 11 1.1.1 AnlogeGrößendrstellung... 11 1.1.2
Gerd Wöstenkühler Grundlgen der Digitltehnik Elementre Komponenten, Funktionen und Steuerungen Inhlt 1 Einleitung... 11 1.1 Anloge unddigitledrstellungsformen... 11 1.1.1 AnlogeGrößendrstellung... 11 1.1.2
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
bei Problemen die Theorie und die Beispiele am Anfang jeder Lerneinheit durcharbeiten
 Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Technische Informatik 2
 TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
Neue Internet Radio Funktion
 XXXXX XXXXX XXXXX /XW-SMA3/XW-SMA4 Neue Internet Rdio Funktion DE EN Dieser drhtlose Lutsprecher ist druf usgelegt, Ihnen den Empfng von Pndor*/Internet-Rdiosendern zu ermöglichen. Bitte echten Sie jedoch,
XXXXX XXXXX XXXXX /XW-SMA3/XW-SMA4 Neue Internet Rdio Funktion DE EN Dieser drhtlose Lutsprecher ist druf usgelegt, Ihnen den Empfng von Pndor*/Internet-Rdiosendern zu ermöglichen. Bitte echten Sie jedoch,
Musterlösung zu Aufgabe 1 (Klassenstufe 9/10)
 Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Kapitel 6 E-Mails senden und empfangen
 Kpitel 6 E-Mils senden und empfngen Sie ist zwr mittlerweile infolge des hohen Spmufkommens ein wenig in Verruf gerten, gehört er immer noch zum Stndrdkommuniktionsmittel des Weürgers: die E-Mil. Zentrle
Kpitel 6 E-Mils senden und empfngen Sie ist zwr mittlerweile infolge des hohen Spmufkommens ein wenig in Verruf gerten, gehört er immer noch zum Stndrdkommuniktionsmittel des Weürgers: die E-Mil. Zentrle
FernUniversität Gesamthochschule in Hagen
 FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
McAfee Firewall Enterprise
 Hnduch für den Schnellstrt Revision B McAfee Firewll Enterprise Version 8.3.x In diesem Hnduch für den Schnellstrt finden Sie llgemeine Anweisungen zum Einrichten von McAfee Firewll Enterprise (im Folgenden
Hnduch für den Schnellstrt Revision B McAfee Firewll Enterprise Version 8.3.x In diesem Hnduch für den Schnellstrt finden Sie llgemeine Anweisungen zum Einrichten von McAfee Firewll Enterprise (im Folgenden
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
QualitŠtskriterien fÿr die betriebliche Gesundheitsfšrderung
 WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
Werben auf askenrico
 Weren uf skenrico skenrico Ihr Online-Reiseführer für Mitteleurop Unser Online-Reiseführer ht eine rsnte Entwicklung zu verzeichnen. Gegründet Ende 2009, zählt er mit üer 10.000 montlichen Besuchern Mitte
Weren uf skenrico skenrico Ihr Online-Reiseführer für Mitteleurop Unser Online-Reiseführer ht eine rsnte Entwicklung zu verzeichnen. Gegründet Ende 2009, zählt er mit üer 10.000 montlichen Besuchern Mitte
Musterlösung zur Musterprüfung 2 in Mathematik
 Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
Ntoneni-be Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen
 FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
Institut für Volkswirtschaftslehre und Wirtschaftspolitik. Prof. Dr. Andreas Thiemer. VWL-Semesterprojekt Nr. 4 WS 2007/2008. Bayessche Lemminge
 Institut für Volkswirtschftslehre und Wirtschftspolitik Prof. Dr. ndres Thiemer VWL-Semesterprojekt Nr. 4 WS 007/008 yessche Lemminge Ein Experiment mit Informtionskskden Unter Mitreit von: Olg eder xel
Institut für Volkswirtschftslehre und Wirtschftspolitik Prof. Dr. ndres Thiemer VWL-Semesterprojekt Nr. 4 WS 007/008 yessche Lemminge Ein Experiment mit Informtionskskden Unter Mitreit von: Olg eder xel
Netzstrategien für Betreiber von Energienetzen Verschmelzung von Technik und Regulierung Teil 4 von 4
 Orgnistion & Mngement Netzstrtegien für Betreier von Energienetzen Verschmelzung von Technik und Regulierung Teil 4 von 4 Quelle: Eisenhns Fotoli.com Der vierte und letzte Teil der Veröffentlichungsreihe
Orgnistion & Mngement Netzstrtegien für Betreier von Energienetzen Verschmelzung von Technik und Regulierung Teil 4 von 4 Quelle: Eisenhns Fotoli.com Der vierte und letzte Teil der Veröffentlichungsreihe
-25/1- DIE RÖHRENDIODE
 -25/1- DIE RÖHRENDIODE ufgben: Messverfhren: Vorkenntnisse: Lehrinhlt: Litertur: ufnhme der Kennlinie einer Röhrendiode und einiger rbeitskennlinien. Bestimmung des Exponenten der Schottky-Lngmuirschen
-25/1- DIE RÖHRENDIODE ufgben: Messverfhren: Vorkenntnisse: Lehrinhlt: Litertur: ufnhme der Kennlinie einer Röhrendiode und einiger rbeitskennlinien. Bestimmung des Exponenten der Schottky-Lngmuirschen
Beispiel-Abiturprüfung
 Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
6.4 Klassendiagramme in UML Übersicht
 6.4 Klssendigrmme in UML Übersicht Mod-6.19 1. UML (Unified Modelling Lnguge): die derzeit wichtigste Sprche zur Modellierung von Systemen 2. Als Zusmmenfssung mehrerer Modellierungssprchen 1997 in der
6.4 Klssendigrmme in UML Übersicht Mod-6.19 1. UML (Unified Modelling Lnguge): die derzeit wichtigste Sprche zur Modellierung von Systemen 2. Als Zusmmenfssung mehrerer Modellierungssprchen 1997 in der
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
Ausbildung zum Passagement-Consultant
 M & MAICONSULTING Mngementbertung Akdemie M MAICONSULTING Mngementbertung & Akdemie MAICONSULTING GmbH & Co. KG Hndschuhsheimer Lndstrße 60 D-69121 Heidelberg Telefon +49 (0) 6221 65024-70 Telefx +49 (0)
M & MAICONSULTING Mngementbertung Akdemie M MAICONSULTING Mngementbertung & Akdemie MAICONSULTING GmbH & Co. KG Hndschuhsheimer Lndstrße 60 D-69121 Heidelberg Telefon +49 (0) 6221 65024-70 Telefx +49 (0)
16.3 Unterrichtsmaterialien
 16.3 Unterrichtsmterilien Vness D.l. Pfeiffer, Christine Glöggler, Stephnie Hhn und Sven Gembll Mteril 1: Alignieren von Nukleotidsequenzen für die Verwndtschftsnlyse Für eine Verwndtschftsnlyse vergleicht
16.3 Unterrichtsmterilien Vness D.l. Pfeiffer, Christine Glöggler, Stephnie Hhn und Sven Gembll Mteril 1: Alignieren von Nukleotidsequenzen für die Verwndtschftsnlyse Für eine Verwndtschftsnlyse vergleicht
Übungsblatt Gleichungssysteme Klasse 8
 Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Entwurf und Realisierung analoger und digitaler Filter
 Signl- und Messwert- Verrbeitung Dr. K. Schefer Entwurf und Relisierung nloger und digitler Filter Im Rhmen dieses Versuchs wollen wir uns mit der Dimensionierung von nlogen und digitlen Filtern und mit
Signl- und Messwert- Verrbeitung Dr. K. Schefer Entwurf und Relisierung nloger und digitler Filter Im Rhmen dieses Versuchs wollen wir uns mit der Dimensionierung von nlogen und digitlen Filtern und mit
Hinweise für den schulischen Umgang mit lese-/rechtschreibschwachen Kindern speziell in der Sekundarstufe I
 Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
Exportmodul Artikel-Nr.: 20208
 Seite 1 / 5 V5.32 Exportmodul Artikel-Nr.: 20208 Erweiterungsmodul für ds ELV-TimeMster Komplettsystem Hndbuch und Beschreibungen Ab der Version 5 befinden sich die Kurznleitung und ds gesmte Hndbuch ls
Seite 1 / 5 V5.32 Exportmodul Artikel-Nr.: 20208 Erweiterungsmodul für ds ELV-TimeMster Komplettsystem Hndbuch und Beschreibungen Ab der Version 5 befinden sich die Kurznleitung und ds gesmte Hndbuch ls
Monte Carlo Methoden. Kapitel 3. 3.1 Simple Sampling
 Kpitel 3 Monte Crlo Methoden Historisch wird der Begriff der Monte Crlo Methode 1947 geprägt [38] 1 und zum ersten MlzweiJhrespäter im Titel einer Veröffentlichung verwendet [39]. Wie der Nme nklingen
Kpitel 3 Monte Crlo Methoden Historisch wird der Begriff der Monte Crlo Methode 1947 geprägt [38] 1 und zum ersten MlzweiJhrespäter im Titel einer Veröffentlichung verwendet [39]. Wie der Nme nklingen
Abb. 2.10: Galvanische Zelle (DANIELL 20 -Element)
 . Der Gleichstromkreis 45.4. Elektrochemische Spnnungsquellen Git mn in ein Lösungsmittel Säuren, Lugen oder Slze, werden deren Moleküle in prweise positiv und negtiv geldene Ionen gesplten (dissoziiert)
. Der Gleichstromkreis 45.4. Elektrochemische Spnnungsquellen Git mn in ein Lösungsmittel Säuren, Lugen oder Slze, werden deren Moleküle in prweise positiv und negtiv geldene Ionen gesplten (dissoziiert)
Versuchsumdruck. Schaltungsvarianten des Operationsverstärkers
 Hchschule STDIENGANG Wirtschftsingenieurwesen Bltt n 6 Aschffenburg Prf. Dr.-Ing.. Bchtler, Armin Huth Versuch 2 Versin. m 23.3.2 Versuchsumdruck Schltungsrinten des Opertinserstärkers Inhlt Verwendete
Hchschule STDIENGANG Wirtschftsingenieurwesen Bltt n 6 Aschffenburg Prf. Dr.-Ing.. Bchtler, Armin Huth Versuch 2 Versin. m 23.3.2 Versuchsumdruck Schltungsrinten des Opertinserstärkers Inhlt Verwendete
EasyMP Slide Converter Bedienungsanleitung
 EsyMP Slide Converter Bedienungsnleitung Inhltsverzeichnis 2 Übersicht über EsyMP Slide Converter EsyMP Slide Converter - Übersicht... 4 Unterstützte Dteitypen für EsyMP Slide Converter... 4 Instlltion
EsyMP Slide Converter Bedienungsnleitung Inhltsverzeichnis 2 Übersicht über EsyMP Slide Converter EsyMP Slide Converter - Übersicht... 4 Unterstützte Dteitypen für EsyMP Slide Converter... 4 Instlltion
