6. Quadratische Gleichungen
|
|
|
- Charlotte Bachmeier
- vor 6 Jahren
- Abrufe
Transkript
1 6. Qudrtische Gleichungen 6.1 Voremerkungen Potenzieren und Wurzelziehen, somit uch Qudrieren und Ziehen der Qudrtwurzel, sind entgegengesetzte Oertionen. Sie heen sich gegenseitig uf. qudrieren Qudrtwurzel ziehen Qudrtwurzeln geen nur us Qudrtzhlen eine gnzzhlige Lösung. Aus llen nderen Zhlen ist die Lösung eine Zhl mit unendlich vielen Dezimlstellen, die im Gegenstz zu Brüchen nicht eriodisch ist Diese nicht eriodischen, unendlich lngen Dezimlzhlen ilden den Grossteil der irrtionlen Zhlen und ergeen zusmmen mit den rtionlen Zhlen die reellen Zhlen (vgl. Kitel 1.). "Qudrierte Zhlen" sind immer ositiv. Sowohl eine ositive wie eine negtive Zhl ergit mit sich seler multiliziert immer eine ositive Zhl. ( ) 5 5 ( ) ( 5) 5 er: -5-5 Qudrtwurzeln können nur us ositiven Zhlen gezogen werden, nur dnn hen sie eine Lösung. ist in unlösr Aus negtiven Zhlen hen Qudrtwurzeln in keine Lösung, denn es git keine reelle Zhl, die mit sich seler multiliziert, eine negtive Zhl ergit. Die Gleichung 5 ht zwei Lösungen: nämlich 1-5 und 5 L { -5 ; 5 } Kontrolle: ( 5) 5 und Normlformen der qudrtischen Gleichungen Qudrtische Gleichungen, d.h. Gleichungen mit, können wie folgt unterschieden werden: rein-qudrtische Gleichung: Die Gleichung enthält nur die Vrile. Beisiel: 5 gemischt-qudrtische Gleichung: Die Gleichung enthält die Vrilen und. Beisiel: Normlformen sind llgemein gehltene Formen, uf die sich uch komlee Aufgenstellungen zurückführen lssen. Folgende Normlformen lssen sich unterscheiden: q-normlform: q 0, q qudrtisches Glied, lineres Glied, q solutes Glied c-normlform: c 0,, c qudrtisches Glied, lineres Glied, c solutes Glied rein-qudrtische Gleichung: - c 0 (oder c) Qudrtische Gleichungen 11
2 6. Lösen von rein-qudrtischen Gleichungen Gleichungen der Form - c 0 zw. c heissen rein-qudrtische Gleichungen. Rein-qudrtische Gleichungen können genu zwei, eine oder keine Lösung hen: zwei Lösungen c > 0 c 1 c, c L { c ; c } eine Lösung ("Doellösung") c , 0 L { 0 } keine Lösung c < 0 unlösr Die Wurzel us einer negtiven Zhl ist in nicht definiert. L { } Beisiele (G ) ) D L { 8 ; 8 } ) ( 11 ) ( - 11 ) 0 D ( 11 ) ( - 11 ) L { 11; 11 } 11 Qudrtische Gleichungen
3 Dozentenseite (mit Lösung) c) 8 D \ { 0 } 7 D \ { 0 } L { -1 ; 1 } L { -1 ; 1 } d) ( - ) ( ) - D D ( - ) ( ) - usmultilizieren zusmmenfssen , L { -1.7 ; 1.7 } L { -1.7 ; 1.7 } e) 0 D D L { } Die. Wurzel us einer negtiven Zhl ist in nicht definiert, lso git es keine Lösung. L { } Qudrtische Gleichungen 115
4 6. Lösen von gemischt-qudrtischen Gleichungen Zum Lösen von gemischt-qudrtischen Gleichungen kennen wir mehrere Methoden. Nicht immer sind lle nwendr oder einfch nwendr. Es lohnt sich deshl, sie lle zu kennen und die jeweils m esten geeignete zu wählen Fktorzerlegung Die Anwendung der Fktorzerlegung geschieht mit den folgenden Schritten: Definitionsmenge estimmen Gleichung in die q-normlform ringen q 0 Linke Seite in zwei Fktoren (mit Summen) zerlegen ( 1 ) ( ) 0 Zum Finden der Werte für 1 und dient folgende Üerlegung: Welche Zhlen 1 und geen miteinnder multiliziert q und zusmmen ddiert? Die Vorzeichen von und q sind zu erücksichtigen Lösungsmenge estimmen L { 1, } Nchweis / Erklärung: Ein Produkt zweier Fktoren ergit nur dnn 0, wenn einer der eiden Fktoren 0 ist ( 1 ) ( ) 0 Der 1. Fktor soll 0 sein d.h Der. Fktor soll 0 sein d.h. 0 Beisiele (G ) ) D ( ) ( - ) 0 Welche Zhlen geen miteinnder drus folgt: 1 -, multiliziert -1 und zusmmen ddiert -1? L { ; } ) ( - 10 ) D , : ( - ) ( - 8 ) 0 Welche Zhlen geen miteinnder drus folgt: 1, 8 multiliziert 16 und zusmmen ddiert -10? L { ; 8 } Diese Methode eignet sich fst nur dnn, wenn die Lösungen us gnzen Zhlen estehen. 116 Qudrtische Gleichungen
5 Dozentenseite (mit Lösung) c) 10 D D ( 5 ) ( - ) 0 Welche Zhlen geen miteinnder drus folgt: 1-5, multiliziert -10 und zusmmen ddiert? L { -5 ; } L { -5 ; } d) 6 ( 8) D \ { -1 } 1 D \ { -1 } 6 ( 8) ( 1 ) 1 ( 1) 6 ( 8) usmultilizieren 6 8-6, : 0 ( ) ( - 6 ) 0 Welche Zhlen geen miteinnder drus folgt: 1 -, 6 multiliziert - und zusmmen ddiert -? L { - ; 6 } L { - ; 6 } Qudrtische Gleichungen 117
6 6.. Qudrtische Ergänzung Die Technik der Fktorzerlegung funktioniert fst nur dnn, wenn die Lösungen gnzzhlig sind. Im ndern Fll ist es rktisch unmöglich, die entsrechenden Summnden der eiden Fktoren heruszufinden. In diesen Fällen führt die Methode der qudrtischen Ergänzung zum Ziel. Sie siert uf den inomischen Formeln. Ds Anwenden dieser Methode ist nhnd von zwei Vrinten erläutert, ei denen sich nur die Schritte und unterscheiden: Üerlegung vi inomische Formeln (mthemtisch korrekt, er etws strkt) "Volkstümliches Rezet" (weniger strkt) Beisiel mit der 1. inomischen Formel (G ) ) D Vrilen und uf die linke, Konstnte uf die rechte Seite der Gleichung trennen (flls der Fktor vor 1 ist, muss die Gleichung noch durch diesen dividiert werden) 8-7 Üerlegung vi inomische Formeln Linke Seite der Gleichung ls Teil einer 1. oder. inomischen Formel uffssen 8-7 ( ) Wert für herusfinden: 8-7 d.h. 8 Fehlendes Glied ( sog. "qudrtische Ergänzung") uf eiden Seiten ddieren -7 ( ) Volkstümliches Rezet Hlieren Sie den Koeffizienten von (d.h. die Zhl vor dem inkl. Vorzeichen), und ddieren Sie uf eiden Seiten der Gleichung ds Qudrt dieser hlierten Zhl. Koeffizienten von (inkl. Vorzeichen) durch dividieren: 8 : Also muss uf eiden Seiten der Gleichung ( ) ddiert werden ( ) Schritte is nlog zur Lösung links Linken Teil ls inomische Formel schreien: ( ) ( ) 9 9-1, 9 Wurzel usrechnen 1, , - -1 L { 7 ; 1 } 118 Qudrtische Gleichungen
7 Dozentenseite (mit Lösung) Beisiel mit der. inomischen Formel (G ) ) D Vrilen und uf die linke, Konstnte uf die rechte Seite der Gleichung trennen : (d.h. durch den Fktor vor dividieren) - 6 Üerlegung vi inomische Formeln Volkstümliches Rezet Linke Seite der Gleichung ls Teil einer 1. oder. inomischen Formel uffssen - 6 Hlieren Sie den Koeffizienten von (d.h. die Zhl vor dem inkl. Vorzeichen), und ddieren Sie uf eiden Seiten der Gleichung ds Qudrt dieser hlierten Zhl. ( - ) d.h. 6 - ( - ) Koeffizienten von durch dividieren: ( -6 ) : - Also muss uf eiden Seiten der Gleichung ( - ) ddiert werden. - 6 ( - ) ( - ) ( - ) Schritte is nlog zur Lösung links ( - ) 9 ( - ) , 11 Wurzel usrechnen 1, , L { 0. ; 6. } c) D D d.h Vrinte: "Volkstümliches Rezet" Koeffizienten von durch dividieren (-1) : -6-1 (-6) - (-6) ( - 6 ) - 6 Schritte is nlog zur Lösung links ( - 6 ) , 6 Wurzel usrechnen 1, 6 1-6, 6 8 L { ; 8 } L { ; 8 } Qudrtische Gleichungen 119
8 Dozentenseite (mit Lösung) d) ( 1 ) ( - ) - 0 D D ( 1 ) ( - ) d.h ( 0.5 ) Vrinte: "Volkstümliches Rezet" Koeffizienten von durch dividieren 1 : Schritte is nlog zur Lösung links ( 0.5 ) , Wurzel usrechnen 1, , L { - ; } L { - ; } e) D D d.h Vrinte: "Volkstümliches Rezet" Koeffizienten von durch dividieren 8 : Schritte is nlog zur Lösung links ( ).5 16 ( ) , 0.5 Wurzel usrechnen 1, , L { -8.5 ; 0.5 } 1 L 8.5 ; 10 Qudrtische Gleichungen
9 6.. q-formel Neen den eiden mthemtischen Methoden der Fktorzerlegung und der qudrtischen Ergänzung git es uch Lösungsmethoden, die uf Formeln sieren: die q- und die c-formel der qudrtischen Gleichungen. Hen wir eine qudrtische Gleichung, ei der vor dem der Fktor 1 steht, lässt sich die q-formel nwenden. Normlform: q 0 1, q Die mthemtische Herleitung der q-formel können Sie im Kitel 6.. nchvollziehen. Allgemeines Lösungsvorgehen: Definitionsmenge estimmen Gleichung in die q-normlform ringen (wenn nötig), und die Werte für und q estimmen Achtung: Die Vorzeichen von und q uch üernehmen. Werte für und q in der Formel einsetzen (inkl. Vorzeichen ) Vrilen 1 und usrechnen Lösungsmenge estimmen Beisiele (G ) ) D Wir estimmen zuerst und q. (flls der Fktor vor 1 ist, muss die Gleichung noch durch diesen dividiert werden) q Die Vorzeichen gehören zu und q dzu Die Werte für und q in der Formel einsetzen:, q -1 1, (-1) Vrilen 1 und usrechnen: 1, 1 1, 5 1, L { 17 ; 1 } Qudrtische Gleichungen 11
10 Dozentenseite (mit Lösung) ) D Gleichung in die q-normlform ringen: : (d.h. durch den Fktor vor dividieren) q Die Werte für und q in der Formel einsetzen: -, q 1 1, Vrilen 1 und usrechnen: 1, , , L { 0.8 ;.6 } c) - 5 D D q 1, ( 5) 1, , , , 9 L { -6 ; 9 } L { -6 ; 9 } 1 Qudrtische Gleichungen
11 Dozentenseite (mit Lösung) d) 1 D \ { 0 ; } D \ { 0 ; } 1 1 ( ) ( - ) zusmmenfssen -, 0 : q 1, 1 1, , 1 0 1, , 1 L { 1 } L { 1 } e) 1 1 D D 1 1-1, : q 1, ( 7) 1, 7 1, 11 1, , L { -1. ; 5. } L { -1. ; 5. } Qudrtische Gleichungen 1
12 1 Qudrtische Gleichungen 6.. Mthemtische Herleitung der q-formel Die Gleichung q 0 soll gelöst werden. Wir wollen eweisen, dss drus die eiden folgenden Lösungen resultieren: q 1 und q 1. Schritt Auf eiden Seiten der Gleichung q sutrhieren q 0 -q. Schritt Auf eiden Seiten der Gleichung ddieren ( qudrtische Ergänzung) q. Schritt Linke Seite in Fktoren zerlegen nch der 1. inomischen Formel: ( ) q. Schritt Wurzel ziehen q 5. Schritt Auf eiden Seiten der Gleichung sutrhieren 1 q q
13 6..5 c-formel Hen wir eine qudrtische Gleichung, ei der vor dem ein Fktor ungleich 0 und ungleich 1 steht, lässt sich die c-formel nwenden. Normlform: c 0 1, c Die mthemtische Herleitung der c-formel können Sie im Kitel 6..6 nchvollziehen. Anmerkung: Mit einer Division durch lässt sich zwr jede c-form einer qudrtischen Gleichung uf die eknnte q-form zurückführen. c 0 : c 0 q : Ist der Fktor vor dem keine einfche ntürliche Zhl oder ergeen die eiden Divisionen keine gnzen Zhlen, so knn die Anwendung der q-formel llerdings komliziert werden : Aus diesem Grund ist zusätzlich zur q-formel uch eine c-formel entwickelt worden. Mit der c-formel lässt sich diese Aufge einfcher lösen ls mit der q-formel. Qudrtische Gleichungen 15
14 Allgemeines Lösungsvorgehen: Definitionsmenge estimmen Gleichung in die c-normlform ringen (wenn nötig) und Werte für, und c estimmen Achtung: Die Vorzeichen von, und c uch üernehmen. Werte für, und c in der Formel einsetzen (inkl. Vorzeichen ) Vrilen 1 und usrechnen Lösungsmenge estimmen Beisiele (G ) ) D Werte für, und c estimmen: c Werte für, und c in der Formel einsetzen: 7, -17, c 6 1, -(-17) (-17) - ( 7 6) 7 Vrilen 1 und usrechnen: 1, , , , L ; ) 5 D \ { - ; } ( - ) 1 ( ) 5 ( ) ( - ) ( ) ( - ) c Werte für, und c in der Formel einsetzen: 5, -1, c -5 1, -(-1) (-1) - ( 5 (-5)) 5 Vrilen 1 und usrechnen: 1, 1 1 ( 1'080) 1, 1 1' , 1-1.8, 6 L { 1.8 ; 6 } Qudrtische Gleichungen
15 Dozentenseite (mit Lösung) c) 1 0 D D c 1, 1 1 ( ) 1, , , , 1 L ; 1 L ; 1 d) 8 5 D D c 1, ( 8 ( 5)) 8 1, , , , 5 8 L 1; 5 8 L 1; 5 8 Qudrtische Gleichungen 17
16 Dozentenseite (mit Lösung) e) 5 5 D \ { ; 5 } D \ { ; 5 } 5 5 (-1) ( - ) ( - 5) ( 1) ( ) ( 1) ( 5) 5 ( 5) ( ) ( 5) ( ) ( ) usmultilizieren zusmmenfssen , : c 1, ( 19) ( 19) ( ) 1, , , , L { 0. ;.5 } L { 0. ;.5 } 18 Qudrtische Gleichungen
17 6..6 Mthemtische Herleitung der c-formel Die Gleichung c 0 soll gelöst werden. Wir wollen eweisen, dss drus die eiden folgenden Lösungen resultieren: 1 c und c 1. Schritt c 0 uf eiden Seiten der Gleichung durch dividieren (Die Division durch ist erlut, weil 0 ist.) c c 0 uf eiden Seiten der Gleichung sutrhieren. Schritt c uf eiden Seiten der Gleichung ddieren c ( qudrtische Ergänzung). Schritt Linke Seite in Fktoren zerlegen nch der 1. inomischen Formel: ( ) c. Schritt Wurzel ziehen c 5. Schritt Wurzel uf der rechten Seite vereinfchen c c c c drus folgt: c 6. Schritt Auf eiden Seiten der Gleichung sutrhieren 1 c 1 c c c Qudrtische Gleichungen 19
18 6..7 Lösungsdiskussion Qudrtische Gleichungen können genu zwei, eine oder keine Lösung hen. Ds hängt dvon, o der Ausdruck in der Wurzel der Lösungsformel grösser, gleich oder kleiner ls 0 ist. Der Ausdruck in der Wurzel heisst Diskriminnte (D) [Diskriminnte Bestimmende]. ei der q-formel: D q ei der c-formel: D c Es ergeen sich somit Fälle (hier ufgezeigt nur n der q-formel): D > 0 zwei Lösungen - 0 1, ( ) 1, 1 1 1, 1 1, 1 1 -, 1 L { ; 1 } y y - D 0 eine Lösung ("Doellösung") 1 0 1, 1 y 5 1, , , , L { 1 } -5 y 1 D < 0 keine Lösung 0 1, 1, 1 1 1, 1 keine Lösung, d in nicht definiert ist L { } y y Nähere Informtionen zur grfischen Vernschulichung der Lösung finden Sie in Kitel Qudrtische Gleichungen
19 6.5 Sätze von Viet Der frnzösische Mthemtiker Viet ( ) ht folgende interessnten Zusmmenhänge uf Grund der q-formel herusgefunden: Die Multiliktion der eiden Lösungen einer qudrtischen Gleichung ergit q. Die Addition der eiden Lösungen einer qudrtischen Gleichung ergit den gleichen Wert wie, er mit umgekehrtem Vorzeichen (lso -). In mthemtischer Schreiweise: Flls q 0 und 1, je Lösungen der Gleichung sind, dnn gilt: 1 q 1 - Die Vorzeichen gehören zu und q dzu Mit den Sätzen von Viet esitzen wir ein gutes Hilfsmittel, um die Korrektheit der Lösungen von qudrtischen Gleichungen zu üerrüfen. ) L { -7 ; 5 } Lösungskontrolle: 1 q ( -7 ) 5-5 Lösungskontrolle, d q ( -7 ) 5 - Lösungskontrolle, d - - ) L { ; 11 } Lösungskontrolle: 1 q 11 Lösungskontrolle, d q Lösungskontrolle, d - - ( -1 ), d.h. - 1 Jede c-normlform knn mit der Division durch in eine q-normlform üerführt werden; drus folgt, dss die Sätze von Viet ngewndt uf die c-form so ussehen: 1 c 1 Die Vorzeichen gehören zu, und c dzu c) L { -0.5 ; } d) 6-0 L { - ; } Lösungskontrolle: 1 c ( -0.5 ) - Lösungskontrolle, d c - Lösungskontrolle: 1 c ( - ) -8 Lösungskontrolle, d c -8 1 ( -0.5 ).5 Lösungskontrolle, d ( - ) - Lösungskontrolle, d 6 - Qudrtische Gleichungen 11
20 6.6 Qudrtische Gleichungen mit zwei Uneknnten Auch ei zwei Vrilen ( und y) knn es im Verluf der Ausrechnung zu qudrtischen Gleichungen kommen. Dies führt dzu, dss die Lösung us zwei Zhlenren esteht. Beisiele (G ) ) (1) 6y 16 ( ) (y ) () y 6 1 D \ { 0 }, D y \ { } (1) 6y 16 ( ) (y ) usmultilizieren 6y 16 (y y 6) usmultilizieren 6y 16 y 6 y 1 6, - y, 1 (1)' 7 y y () y 6 1 ( y - 6 ) (y 6) (y 6) usmultilizieren 6y 18 y 6 6 ()' 6y 18 y Gleichsetzungsverfhren (Gleichungen (1)' und ()' gleichsetzen) 7 y 6y 18 -, - y, y 1 : y 1 Ausrechnen der 1. Vrilen ( in Gleichung (1)' einsetzen) y 1 y 1 7 y y 7 (y 1) 6y 1 y (y 1) usmultilizieren 8y 98 6y 1 8y 8y zusmmenfssen y 110 8y 8y - y, 110 8y 6y : y 1y 55 0 y 1, ( 1) ( 1) ( 55) y 1, y 1.75, y 5 y 1, y 1, Ausrechnen der. Vrilen (y 1, in die Umformung von Schritt einsetzen) y 1 einsetzen: y y einsetzen: y L {( 1.75) ; ( 5 ) } 1 Qudrtische Gleichungen
21 Dozentenseite (mit Lösung) ) (1) y 1 () ( ) y 5 D D (1) y 1 : (1)' 1 y () ( ) y 5 6 y 5 5 ()' y 11 Gleichsetzungsverfhren (Gleichungen (1)' und ()' gleichsetzen) c Ausrechnen der 1. Vrilen 1, ( 1) 1, , , , - Ausrechnen der. Vrilen (hier: 1, in Gleichung ()' einsetzen) 1 einsetzen: 11 y 1 (.5) 11 y 1 y1 1 einsetzen: 11 y ( ) 11 y 7 y L { ( -.5 ) ; ( - 7 ) } L { ( -.5 ) ; ( - 7 ) } Qudrtische Gleichungen 1
22 Dozentenseite (mit Lösung) c) (1) y () 1 y D \ { -1 } \ { - ; 0 } D \ { -1 }, D y \ { - ; 0 } oder D \ { -1 } \ { - ; 0 } (1) y () ( - ) ()' y 1 y Additionsverfhren (1) y ()' y y 6 y 5 8 Ausrechnen der 1. Vrilen 6 y ( y ) y y (y ) 6y y (y ) usmultilizieren y 6 6y y 6y zusmmenfssen 9y 6 y 6y y, 6y y y 6 0 : y y 0 y - 1y - 0 q y 1, 1 1 ( ) y 1, y 1, y 1-1, y Ausrechnen der. Vrilen (hier: y 1, in Gleichung (1) einsetzen) y 1 einsetzen: (1 1) y einsetzen: ( 1) L ( 1) ; 1 L ( 1) ; 1 1 Qudrtische Gleichungen
23 6.7 Qudrtische Gleichungen mit Prmetern Zusätzlich zu den Konstnten knn eine qudrtische Gleichung uch noch Prmeter enthlten. Ds Anwenden der vier Lösungsmethoden leit grundsätzlich gleich, erfordert er oft ein hohes Mss n Konzentrtion. Beisiele (G ) ) - 0 Lösungsmethode "Fktorzerlegung" D ( - ) ( - ) 0 L { ; } ) Lösungsmethode "q-formel" D, q , ( 0.75 ) , 0.5 L { 1.5 ; 0.5 } c) ( ) 0 Lösungsmethode "c-formel" D, ( ), c 1, ( 1 ) ( ) ( ( ) ), 8 L ; 0 Qudrtische Gleichungen 15
24 Dozentenseite (mit Lösung) d) D D ( - 1 ) - 0 ( - 1 ) - 0 q 1, 1 1 ( ) 1, 1 1 1, 1, , 1 ( 1) ( 1) 1, L { - ; 1 } L { - ; 1 } e) 1 D 0 D 0 1 -, ( 1) ( ) 0 c 1, ( 1) ( 1) 1, L 1, 1, 1 ; ( 1) 1 ( ) 1 1 L ; Achtung: Dmit keine Division durch 0 entsteht, folgt: 0. Ist in D ereits so festgelegt. Es entfällt somit, 0 ei der Lösungsmenge zu ergänzen Qudrtische Gleichungen
Nullstellen quadratischer Gleichungen
 Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Wurzeln. bestimmen. Dann braucht man Wurzeln. Treffender müsste man von Quadratwurzeln sprechen. 1. Bei Quadraten, deren Fläche eine Quadratzahl ist,
 Seitenlängen von Qudrten lssen sich mnchml sehr leicht und mnchml etws schwerer Wurzeln bestimmen. Dnn brucht mn Wurzeln. Treffender müsste mn von Qudrtwurzeln sprechen. Sie stehen in enger Beziehung zu
Seitenlängen von Qudrten lssen sich mnchml sehr leicht und mnchml etws schwerer Wurzeln bestimmen. Dnn brucht mn Wurzeln. Treffender müsste mn von Qudrtwurzeln sprechen. Sie stehen in enger Beziehung zu
Grundwissen. Die Menge der reellen Zahlen 0 =0. Beispiele
 Grundwissen Klsse 9 Die Menge der reellen Zhlen Die Umkehrung des Qudrierens wird für nicht negtive Zhlen ls Ziehen der Wurzel oder Rdizieren ezeichnet. Die Qudrtwurzel us (kurz: Wurzel us ) ist dei die
Grundwissen Klsse 9 Die Menge der reellen Zhlen Die Umkehrung des Qudrierens wird für nicht negtive Zhlen ls Ziehen der Wurzel oder Rdizieren ezeichnet. Die Qudrtwurzel us (kurz: Wurzel us ) ist dei die
5 Gleichungen (1. Grades)
 Mthemtik PM Gleichungen (. Grdes) Gleichungen (. Grdes). Einführung Betrchtet mn und (, Q) und vergleicht sie miteinnder, so git es Möglichkeiten:. > ist grösser ls. = ist gleich gross wie. < ist kleiner
Mthemtik PM Gleichungen (. Grdes) Gleichungen (. Grdes). Einführung Betrchtet mn und (, Q) und vergleicht sie miteinnder, so git es Möglichkeiten:. > ist grösser ls. = ist gleich gross wie. < ist kleiner
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
ARBEITSBLATT 5L-6 FLÄCHENBERECHNUNG MITTELS INTEGRALRECHNUNG
 Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Mathe Warm-Up, Teil 1 1 2
 Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Mthe Wrm-Up, Teil 1 1 2 HEUTE: 1. Elementre Rechenopertionen: Brüche, Potenzen, Logrithmus, Wurzeln 2. Summen- und Produktzeichen 3. Gleichungen/Ungleichungen 1 orientiert sich n den Kpiteln 3,4,6,8 des
Bruchterme I. Definitionsmenge eines Bruchterms
 Bruchterme I Definitionsmenge eines Bruchterms Alle zulässigen Einsetzungen in einen Bruchterm ilden die Definitionsmenge D. Einsetzungen, für die der Nenner Null wird, gehören nicht zur Definitionsmenge.
Bruchterme I Definitionsmenge eines Bruchterms Alle zulässigen Einsetzungen in einen Bruchterm ilden die Definitionsmenge D. Einsetzungen, für die der Nenner Null wird, gehören nicht zur Definitionsmenge.
Exponentialgleichungen 70 Exponentialgleichungen mit Ergebnissen und ausführlichen Lösungsweg
 Übungen zum Kurs Eponentilgleichungen Eponentilgleichungen 70 Eponentilgleichungen mit Ergebnissen und usführlichen Lösungsweg 7.technisch verbesserte Auflge vom.09.007 (Sonderzeichen wurden teilweise
Übungen zum Kurs Eponentilgleichungen Eponentilgleichungen 70 Eponentilgleichungen mit Ergebnissen und usführlichen Lösungsweg 7.technisch verbesserte Auflge vom.09.007 (Sonderzeichen wurden teilweise
RESULTATE UND LÖSUNGEN
 TG TECHNOLOGISCHE GRUNDLAGEN Kpitel 3 Mthemtik Kpitel 3.2 Alger Grundrechenrten RESULTATE UND LÖSUNGEN Verfsser: Hns-Rudolf Niedererger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausge:
TG TECHNOLOGISCHE GRUNDLAGEN Kpitel 3 Mthemtik Kpitel 3.2 Alger Grundrechenrten RESULTATE UND LÖSUNGEN Verfsser: Hns-Rudolf Niedererger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausge:
Übungen zu Wurzeln III
 A.Nenner rtionl mchen: Nenner ist Qudrtwurzel: 5 bc 1.).).).) 5.) 1 15 9 bc.).) 8.) 9.) 10.) 5 5 B.Nenner rtionl mchen: Nenner ist höhere Wurzel: 1 1 9 5 1 1.).).).) 5.).) 5 C.Nenner rtionl mchen: Nenner
A.Nenner rtionl mchen: Nenner ist Qudrtwurzel: 5 bc 1.).).).) 5.) 1 15 9 bc.).) 8.) 9.) 10.) 5 5 B.Nenner rtionl mchen: Nenner ist höhere Wurzel: 1 1 9 5 1 1.).).).) 5.).) 5 C.Nenner rtionl mchen: Nenner
Orientierungstest Mathematische Grundlagen
 Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mthemtik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufge 69. Quizz Integrle. Es sei Höhere Mthemtik für Informtiker II (Sommersemester
4 Die rationalen Zahlen
 4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
4 Die rtionlen Zhlen Der Ring der gnzen Zhlen ht den Mngel, dß nicht jede Gleichung = X, 0 innerhl Z lösr ist. (Z.B. ist 1 = 2 X unlösr in Z). Zu seiner Beseitigung erweitert mn den Zhlereich zum Körper
Mathematik schriftlich
 WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
WS KV Chur Abschlussprüfungen 00 für die Berufsmtur kufmännische Richtung Mthemtik schriftlich LÖSUNGEN Kndidtennummer Nme Vornme Dtum der Prüfung Bewertung mögliche erteilte Punkte Punkte. Aufgbe 0. Aufgbe
Verlauf Material LEK Glossar Lösungen. Das Wurzelwerk ein Spiel. Dr. Heinrich Schneider, Wien
 Reihe S 1 Verluf Mteril Ds Wurzelwerk ein Spiel Dr. Heinrich Schneider, Wien Klsse 10 Duer Inhlt Ihr Plus vriel, weil Sie Spielkrten weglssen können (Gesmtumfng: 9 Stunden) Wurzeln in jeglicher Form; teilweise
Reihe S 1 Verluf Mteril Ds Wurzelwerk ein Spiel Dr. Heinrich Schneider, Wien Klsse 10 Duer Inhlt Ihr Plus vriel, weil Sie Spielkrten weglssen können (Gesmtumfng: 9 Stunden) Wurzeln in jeglicher Form; teilweise
Quadratische Funktionen
 Qudrtische Funktionen Definition: Eine Funktion mit der Gleichung y = c (,, c R; 0) heißt qudrtische Funktion oder Funktion. Grdes. qudrtisches Glied;...lineres Glied; c...solutes Glied Der Grph einer
Qudrtische Funktionen Definition: Eine Funktion mit der Gleichung y = c (,, c R; 0) heißt qudrtische Funktion oder Funktion. Grdes. qudrtisches Glied;...lineres Glied; c...solutes Glied Der Grph einer
Differenzial- und Integralrechnung III
 Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Differenzil- und Integrlrechnung III Riner Huser April 2012 1 Einleitung 1.1 Polynome und Potenzfunktionen Die Polynome oder Polynomfunktionen lssen sich durch die endliche Anzhl von n+1 Prmetern i R in
Vorkurs Mathematik DIFFERENTIATION
 Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
Kleine Algebra-Formelsammlung
 Immnuel-Knt-Gymnsium Heiligenhus Gierhrt Kleine Alger-Formelsmmlung Mittelstufe (is Klsse 0) Drgestellt sin ie wichtigsten Fkten un Gesetze, woei iverse Ausnhmeregeln wie z.b. s Verot er Division urch
Immnuel-Knt-Gymnsium Heiligenhus Gierhrt Kleine Alger-Formelsmmlung Mittelstufe (is Klsse 0) Drgestellt sin ie wichtigsten Fkten un Gesetze, woei iverse Ausnhmeregeln wie z.b. s Verot er Division urch
R. Brinkmann http://brinkmann-du.de Seite 1 17.11.2010
 R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
R. rinkmnn http://rinkmnn-du.de Seite 7..2 Grundegriffe der Vektorrehnung Vektor und Sklr Ein Teil der in Nturwissenshft und Tehnik uftretenden Größen ist ei festgelegter Mßeinheit durh die nge einer Mßzhl
Mathematik Brückenkurs
 Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Mthemtik Brückenkurs im Fchbereich Informtik & Elektrotechnik Rumpfskript V7 Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Inhltsverzeichnis Mengen...
Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Mthemtik Brückenkurs im Fchbereich Informtik & Elektrotechnik Rumpfskript V7 Rumpfskript zur Vorlesung Mthemtik-Brückenkurs /86 Inhltsverzeichnis Mengen...
Bruchterme. Franz Embacher
 mthe online Skripten http://www.mthe-online.t/skripten/ Bruchterme Frnz Emcher Fkultät für Mthemtik der Universität Wien E-mil: frnz.emcher@univie.c.t WWW: http://homepge.univie.c.t/frnz.emcher/ In diesem
mthe online Skripten http://www.mthe-online.t/skripten/ Bruchterme Frnz Emcher Fkultät für Mthemtik der Universität Wien E-mil: frnz.emcher@univie.c.t WWW: http://homepge.univie.c.t/frnz.emcher/ In diesem
Grundwissen Jahrgangsstufe 9
 Grundwissen Jhrgngsstufe 9 GM 9. Qudrtwurzeln und die Menge der reellen Zhlen QUADRATWURZELN Unter der Qudrtwurzel us einer Zhl (kurz: Wurzel us, Schreibweise ) versteht mn diejenige nichtnegtive Zhl,
Grundwissen Jhrgngsstufe 9 GM 9. Qudrtwurzeln und die Menge der reellen Zhlen QUADRATWURZELN Unter der Qudrtwurzel us einer Zhl (kurz: Wurzel us, Schreibweise ) versteht mn diejenige nichtnegtive Zhl,
Berechnung von Flächen unter Kurven
 Berechnung von Flächen unter Kurven Es soll die Fläche unter einer elieigen (stetigen) Kurve erechnet werden. Dzu etrchten wir die (sog.) Flächenfunktion, mit der die zu erechnende Fläche qusi ngenähert
Berechnung von Flächen unter Kurven Es soll die Fläche unter einer elieigen (stetigen) Kurve erechnet werden. Dzu etrchten wir die (sog.) Flächenfunktion, mit der die zu erechnende Fläche qusi ngenähert
Grundlagen in Mathematik für die 1. Klassen der HMS und der FMS
 Grundlgen in Mthemtik für die. Klssen der HMS und der FMS Einleitung In der Mthemtik wird häufig uf bereits Gelerntem und Beknntem ufgebut. Wer die Grundlgen nicht beherrscht, ht deshlb oft Mühe und Schwierigkeiten,
Grundlgen in Mthemtik für die. Klssen der HMS und der FMS Einleitung In der Mthemtik wird häufig uf bereits Gelerntem und Beknntem ufgebut. Wer die Grundlgen nicht beherrscht, ht deshlb oft Mühe und Schwierigkeiten,
Brückenkurs Mathematik
 Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Bruchterme und gebrochen rationale Funktionen ================================================================== Der Quotient zweier Terme
 Bruchterme und gebrochen rtionle Funktionen Der Quotient zweier Terme Es ist ist 3 : 4 3 und. 4 : 3 4 3 4 Dehnt mn die Bruchschreibweise uf Terme us, dnn erhält mn sog. Bruchteme. ² ( + ) : (3 + 4) + 3
Bruchterme und gebrochen rtionle Funktionen Der Quotient zweier Terme Es ist ist 3 : 4 3 und. 4 : 3 4 3 4 Dehnt mn die Bruchschreibweise uf Terme us, dnn erhält mn sog. Bruchteme. ² ( + ) : (3 + 4) + 3
v P Vektorrechnung k 1
 Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
- 1 - VB Inhaltsverzeichnis
 - - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Theoretische Informatik und Logik Übungsblatt 2 (2013S) Lösung
 Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
Theoretische Informtik und Logik Üungsltt 2 (2013S) en Aufge 2.1 Geen Sie jeweils eine kontextfreie Grmmtik n, welche die folgenden Sprchen erzeugt, sowie einen Aleitungsum für ein von Ihnen gewähltes
1.6 Bruchterme. 1 Einführung und Repetition 2. 2 Multiplikation und Division von Bruchtermen 3. 3 Die Addition von zwei Bruchtermen-Methode I 3
 .6 Bruchterme Inhltsverzeichnis Einführung und Repetition 2 2 Multipliktion und Division von Bruchtermen 3 3 Die Addition von zwei Bruchtermen-Methode I 3 4 Doppelbrüche 5 5 Die Addition von zwei Bruchtermen
.6 Bruchterme Inhltsverzeichnis Einführung und Repetition 2 2 Multipliktion und Division von Bruchtermen 3 3 Die Addition von zwei Bruchtermen-Methode I 3 4 Doppelbrüche 5 5 Die Addition von zwei Bruchtermen
10 Anwendungen der Integralrechnung
 9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Brückenkurs Lineare Gleichungssysteme und Vektoren
 Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
Bestimmtes (Riemannsches) Integral / Integral als Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhalb bestimmter Grenzen
 III. Integrlrechnung : Bestimmtes (Riemnnsches Integrl / Integrl ls Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhl estimmter Grenzen yf( y n y n ( Δ Berechnung der Fläche A unter
III. Integrlrechnung : Bestimmtes (Riemnnsches Integrl / Integrl ls Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhl estimmter Grenzen yf( y n y n ( Δ Berechnung der Fläche A unter
Inhalt: Die vorliegenden Folienvorlagen enthalten folgende Elemente:
 Inhlt: 1 Qudrt und Rechteck Prllelogrmm 3 Dreieck 4 Trpez 5 Drchen und Rute 6 Exkurs: Höhen zeichnen 7 heckliste Kopiervorlge: Formeln herleiten 8 Hinweise zur Benutzung 6 10 13 17 0 3 4 Die vorliegenden
Inhlt: 1 Qudrt und Rechteck Prllelogrmm 3 Dreieck 4 Trpez 5 Drchen und Rute 6 Exkurs: Höhen zeichnen 7 heckliste Kopiervorlge: Formeln herleiten 8 Hinweise zur Benutzung 6 10 13 17 0 3 4 Die vorliegenden
5.6 Additionsverfahren
 5.6 Additiosverfhre Prizip Die eide Gleihuge werde so umgeformt, dss ei der Additio der eide Gleihuge eie Vrile wegfällt. Es müsse h der Umformug lso i eide Gleihuge gleih viele x oder gleih viele y (er
5.6 Additiosverfhre Prizip Die eide Gleihuge werde so umgeformt, dss ei der Additio der eide Gleihuge eie Vrile wegfällt. Es müsse h der Umformug lso i eide Gleihuge gleih viele x oder gleih viele y (er
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Logarithmus - Übungsaufgaben. I. Allgemeines
 Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Teilbarkeitsregeln. 6.1 Grundwissen Mathematik Algebra Klasse 6. Teilbarkeit durch 2: Eine Zahl ist durch 2 teilbar, wenn die Endziffer gerade ist.
 6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
 Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen Mathematik 8. Klasse. Eigenschaften Besonderheiten - Beispiele
 Themen Direkte Proportionlität Eigenschften Besonderheiten - Beispiele Zwei Größen und y heißen direkt proportionl, wenn gilt: Zum k-fchen Wert von gehört der k-fche Wert von y; Der Quotient q = y ht für
Themen Direkte Proportionlität Eigenschften Besonderheiten - Beispiele Zwei Größen und y heißen direkt proportionl, wenn gilt: Zum k-fchen Wert von gehört der k-fche Wert von y; Der Quotient q = y ht für
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Matrizen und Determinanten
 Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
A.25 Stetigkeit und Differenzierbarkeit ( )
 A.5 Stetigkeit / Differenzierbrkeit A.5 Stetigkeit und Differenzierbrkeit ( ) Eine Funktion ist wenn die Kurve nicht unterbrochen wird, lso wenn mn sie zeichnen knn, ohne den Stift vom Bltt bzusetzen.
A.5 Stetigkeit / Differenzierbrkeit A.5 Stetigkeit und Differenzierbrkeit ( ) Eine Funktion ist wenn die Kurve nicht unterbrochen wird, lso wenn mn sie zeichnen knn, ohne den Stift vom Bltt bzusetzen.
MATHEMATIK GRUNDWISSEN KLASSE 5
 MATHEMATIK GRUNDWISSEN KLASSE 5 Them NATÜRLICHE ZAHLEN Zählen und Ordnen Ntürliche Zhlen werden zum Zählen und Ordnen verwendet Stefn ist beim 100m-Luf ls 2. ins Ziel gekommen. Große Zhlen und Zehnerpotenzen
MATHEMATIK GRUNDWISSEN KLASSE 5 Them NATÜRLICHE ZAHLEN Zählen und Ordnen Ntürliche Zhlen werden zum Zählen und Ordnen verwendet Stefn ist beim 100m-Luf ls 2. ins Ziel gekommen. Große Zhlen und Zehnerpotenzen
Analysis mit dem Voyage 1
 Anlysis mit dem Voyge 1 1. Kurvendiskussion Gegeben ist die Funktionschr Den Nenner erhält mn mit Hilfe der Funktion getdenom. Zeros liefert die Nullstellen des Nenners und dmit die Werte, die us dem Definitionsbereich
Anlysis mit dem Voyge 1 1. Kurvendiskussion Gegeben ist die Funktionschr Den Nenner erhält mn mit Hilfe der Funktion getdenom. Zeros liefert die Nullstellen des Nenners und dmit die Werte, die us dem Definitionsbereich
Einführung in die Lineare Algebra
 Einführung in die Linere Alger Linere Gleichungssysteme Dieses Kpitels dient zur Motivtion und Vorereitung der systemtischen Drstellung. Wir hen dfür ds wichtigste Prolem der elementren lineren Alger gewählt,
Einführung in die Linere Alger Linere Gleichungssysteme Dieses Kpitels dient zur Motivtion und Vorereitung der systemtischen Drstellung. Wir hen dfür ds wichtigste Prolem der elementren lineren Alger gewählt,
Reader. für den Einsatz in der Wiederholungsphase im Mathematikunterricht der Jahrgangsstufe 11
 Reder für den Einstz in der Wiederholungsphse im Mthemtikunterricht der Jhrgngsstufe Anhng zur schriftlichen Husrbeit zur Zweiten Sttsprüfung für ds Lehrmt n öffentlichen Schulen von Andres Rschke Vorwort
Reder für den Einstz in der Wiederholungsphse im Mthemtikunterricht der Jhrgngsstufe Anhng zur schriftlichen Husrbeit zur Zweiten Sttsprüfung für ds Lehrmt n öffentlichen Schulen von Andres Rschke Vorwort
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil I: Theorie. Michael Buhlmann
 Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Facharbeit über algebraische Gleichungen vierten Grades
 Fchrbeit über lgebrische Gleichungen vierten Grdes inkl. der Crdni schen Formeln und dem Beweis der Formeln. Verfßt von Ing. Wlter Höhlhubmer im Oktober ergänzt im Juli und August und erweitert im Dez.
Fchrbeit über lgebrische Gleichungen vierten Grdes inkl. der Crdni schen Formeln und dem Beweis der Formeln. Verfßt von Ing. Wlter Höhlhubmer im Oktober ergänzt im Juli und August und erweitert im Dez.
Grundwissen Abitur Analysis
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
hat genau eine eindeutig bestimmte Lösung, wenn für die Determinante der Koeffizientenmatrix gilt:
 1 Determinnten Die Determinnte einer qudrtischen Mtrix ist eine reelle Zhl. Sie ermöglicht insbesondere eine Aussge über die Existenz der inversen Mtrix bzw. über die Lösbrkeit von lineren leichungssystemen.
1 Determinnten Die Determinnte einer qudrtischen Mtrix ist eine reelle Zhl. Sie ermöglicht insbesondere eine Aussge über die Existenz der inversen Mtrix bzw. über die Lösbrkeit von lineren leichungssystemen.
Inhalt: Die vorliegenden Folienvorlagen enthalten folgende Elemente:
 Inhlt: 1. Die Bedeutung von Vriblen....................................... 2. Addition und Subtrktion gleichrtiger Terme............................ 3. Multipliktion und Division von einfchen Termen.........................
Inhlt: 1. Die Bedeutung von Vriblen....................................... 2. Addition und Subtrktion gleichrtiger Terme............................ 3. Multipliktion und Division von einfchen Termen.........................
Themenbereich: Kongruenzsätze Seite 1 von 6
 Themenereich: Kongruenzsätze Seite 1 von 6 Lernziele: - Kenntnis der genuen Formulierung der Kongruenzsätze - Kenntnis der edeutung der Kongruenzsätze - Fähigkeit, die Kongruenzssätze gezielt zur egründung
Themenereich: Kongruenzsätze Seite 1 von 6 Lernziele: - Kenntnis der genuen Formulierung der Kongruenzsätze - Kenntnis der edeutung der Kongruenzsätze - Fähigkeit, die Kongruenzssätze gezielt zur egründung
Übungsblatt Gleichungssysteme Klasse 8
 Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Mathematisches Grundwissen...2 Summen und Differenzen...2 Rechnen mit Brüchen...3 Addition und Subtraktion...3 Erweitern / Kürzen...
 Mthemtisches Grundwissen... Summen und Differenzen... Rechnen mit Brüchen... Addition und Sutrktion... Erweitern / Kürzen... Multipliktion / Division... Aufgen - Rechnen mit Brüchen... Lösungen - Rechnen
Mthemtisches Grundwissen... Summen und Differenzen... Rechnen mit Brüchen... Addition und Sutrktion... Erweitern / Kürzen... Multipliktion / Division... Aufgen - Rechnen mit Brüchen... Lösungen - Rechnen
Repetitionsaufgaben Exponential-und Logarithmusfunktion
 Repetitionsufgben Eponentil-und Logrithmusfunktion Inhltsverzeichnis A) Vorbemerkungen B) Lernziele C) Eponentilfunktionen mit Beispielen 2 D) Aufgben Ep.fkt. mit Musterlösungen 6 E) Logrithmusfunktionen
Repetitionsufgben Eponentil-und Logrithmusfunktion Inhltsverzeichnis A) Vorbemerkungen B) Lernziele C) Eponentilfunktionen mit Beispielen 2 D) Aufgben Ep.fkt. mit Musterlösungen 6 E) Logrithmusfunktionen
dem Verfahren aus dem Beweis zu Satz 2.20 erhalten wir zunächst die folgenden beiden ε-ndeas für die Sprachen {a} {b} und {ε} {a} +
 Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Lösungen zu Üungsltt 3 Aufge 1. Es gilt L(( ) ) = ({} {}) {} = ({} {}) ({} {} + ). Mit dem Verfhren us dem Beweis zu Stz 2.20 erhlten wir zunächst die folgenden eiden -NDEAs für die Sprchen {} {} und {}
Erweitern. a b. bd + bc. bd = ad+bc. bei ganzzahligem Nenner: Hauptnenner (= kgv der Nenner), z.b. 4 6 + 3 4 = 8 12 + 9. a d = ac
 F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
Grundwissen 7. Jahrgangsstufe 1. Symmetrie Wissen Können Beispiele a) Achsenspiegelung : Symmetrieachse Mittelsenkrechte Winkelhalbierende
 Grundwissen 7. Jhrgngsstufe 1. Symmetrie ) chsenspiegelung : Symmetriechse Mittelsenkrechte Winkelhlbierende Konstruktion Spiegelpunkt, Spiegelchse Mittelsenkrechte: Winkelhlbierende: Lot: Eigenschften
Grundwissen 7. Jhrgngsstufe 1. Symmetrie ) chsenspiegelung : Symmetriechse Mittelsenkrechte Winkelhlbierende Konstruktion Spiegelpunkt, Spiegelchse Mittelsenkrechte: Winkelhlbierende: Lot: Eigenschften
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Spiele und logische Komplexitätsklassen
 Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
Grundwissen Mathematik 5/1
 1 Wichtige Symole Grundwissen Mthemtik 5/1 Wichtige Symole Rechenrten Qudrtzhlen IN Menge der ntürlichen Zhlen { 1; ; 3; 4;... } IN 0 Menge der ntürlichen Zhlen einschließlich der Null {0; 1; ; 3; 4;...
1 Wichtige Symole Grundwissen Mthemtik 5/1 Wichtige Symole Rechenrten Qudrtzhlen IN Menge der ntürlichen Zhlen { 1; ; 3; 4;... } IN 0 Menge der ntürlichen Zhlen einschließlich der Null {0; 1; ; 3; 4;...
GRUNDWISSEN MATHEMATIK. Gymnasium Ernestinum Coburg Fachschaft Mathematik
 GRUNDWISSEN MTHEMTIK Gymnsium Ernestinum Coburg Fchschft Mthemtik GM 5.1 Zhlen und Mengen Grundwissen Jhrgngsstufe 5 Mengen werden in der Mthemtik mit geschweiften Klmmern geschrieben: Menge der ntürlichen
GRUNDWISSEN MTHEMTIK Gymnsium Ernestinum Coburg Fchschft Mthemtik GM 5.1 Zhlen und Mengen Grundwissen Jhrgngsstufe 5 Mengen werden in der Mthemtik mit geschweiften Klmmern geschrieben: Menge der ntürlichen
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
Musterlösung zur Musterprüfung 2 in Mathematik
 Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
Musterlösung zur Musterprüfung in Mthemtik Diese Musterlösung enthält usführliche Lösungen zu llen Aufgben der Musterprüfung in Mthemtik sowie Hinweise zum Selbstlernen. Literturhinweise ) Bosch: Brückenkurs
4 Stetigkeit. 4.1 Intervalle
 4 Stetigkeit Der Grenzwertbegriff für Zhlenfolgen lässt sich uf Funktionen übertrgen. Funktionen (oder Abbildungen) wren bereits im Kpitel über Mengen ufgetreten. Hier wird nun der Fll betrchtet, dss Definitionsbereich
4 Stetigkeit Der Grenzwertbegriff für Zhlenfolgen lässt sich uf Funktionen übertrgen. Funktionen (oder Abbildungen) wren bereits im Kpitel über Mengen ufgetreten. Hier wird nun der Fll betrchtet, dss Definitionsbereich
Grundwissen Jahrgangsstufe 7
 GM 7.1 chsensymmetrie Grundwissen Jhrgngsstufe 7 Definition Zwei unkte liegen symmetrisch bezüglich einer chse, wenn ihre Verbindungsstrecke von der chse senkrecht hlbiert wird. M und liegen symmetrisch
GM 7.1 chsensymmetrie Grundwissen Jhrgngsstufe 7 Definition Zwei unkte liegen symmetrisch bezüglich einer chse, wenn ihre Verbindungsstrecke von der chse senkrecht hlbiert wird. M und liegen symmetrisch
Mathematik fu r Ingenieure (Maschinenbau und Sicherheitstechnik) 2. Semester Apl. Prof. Dr. G. Herbort Dr. T. Pawlaschyk. SoSe16 Arbeitsheft Blatt 3
 Mthemtik fu r Ingenieure (Mschinenu und Sicherheitstechnik). Semester Apl. Prof. Dr. G. Herort Dr. T. Pwlschyk SoSe6 Areitsheft Bltt Hinweis: Besuchen Sie die Vorlesung und vervollst ndigen Sie Areitsheft.
Mthemtik fu r Ingenieure (Mschinenu und Sicherheitstechnik). Semester Apl. Prof. Dr. G. Herort Dr. T. Pwlschyk SoSe6 Areitsheft Bltt Hinweis: Besuchen Sie die Vorlesung und vervollst ndigen Sie Areitsheft.
t ) - auch Zerfallsrate genannt - ist
 Differentilgleichungen - Ausgewählte Proleme us der Phsik Beisiel: Rdioktiver Zerfll Eine gnze Reihe hsiklischer Erscheinungen lässt sich unter dem Stichwort Zerfll ngeregter Zustände einordnen. Ein Beisiel
Differentilgleichungen - Ausgewählte Proleme us der Phsik Beisiel: Rdioktiver Zerfll Eine gnze Reihe hsiklischer Erscheinungen lässt sich unter dem Stichwort Zerfll ngeregter Zustände einordnen. Ein Beisiel
FernUniversität Gesamthochschule in Hagen
 FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
 S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
Umstellen von Formeln und Gleichungen
 Umstellen von Formeln und Gleihungen. Ds Zusmmenfssen von Termen edeutet grundsätzlih ein Ausklmmern, uh wenn mn den Zwishenshritt niht immer ufshreit. 4 6 = (4 6) =. Steht eine Vrile, nh der ufgelöst
Umstellen von Formeln und Gleihungen. Ds Zusmmenfssen von Termen edeutet grundsätzlih ein Ausklmmern, uh wenn mn den Zwishenshritt niht immer ufshreit. 4 6 = (4 6) =. Steht eine Vrile, nh der ufgelöst
2. Klausur in K2 am
 Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Falls die Werte von X als Ergebnisse eines Zufallsvorgangs resultieren, wird X zu einer stetigen Zufallsvariable.
 Sttistik I für Sttistiker, Mthemtiker und Informtiker Lösungen zu Bltt 11 Gerhrd Tutz, Jn Ulbricht, Jn Gertheiss WS 7/8 Theorie: Stetige Zufllsvriblen Begriff Stetigkeit: Eine Vrible oder ein Merkml X
Sttistik I für Sttistiker, Mthemtiker und Informtiker Lösungen zu Bltt 11 Gerhrd Tutz, Jn Ulbricht, Jn Gertheiss WS 7/8 Theorie: Stetige Zufllsvriblen Begriff Stetigkeit: Eine Vrible oder ein Merkml X
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
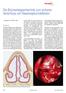 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Public-Key-Verfahren: Diffie-Hellmann und ElGamal
 Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Seminar zum anorganisch-chemischen Praktikum I. Quantitative Analyse. Prof. Dr. M. Scheer Patrick Schwarz
 Seminr zum norgnish-hemishen Prktikum I Quntittive Anlyse Prof. Dr. M. Sheer Ptrik Shwrz itertur A. F. Hollemn, E. Wierg, ehruh der Anorgnishen Chemie, de Gruyter Verlg, Berlin, New York (Ahtung, neue
Seminr zum norgnish-hemishen Prktikum I Quntittive Anlyse Prof. Dr. M. Sheer Ptrik Shwrz itertur A. F. Hollemn, E. Wierg, ehruh der Anorgnishen Chemie, de Gruyter Verlg, Berlin, New York (Ahtung, neue
Grundwissen am Ende der 9. Jahrgangsstufe. Wahlpflichtfächergruppe I
 Grundwissen m Ende der 9. Jhrgngsstufe Whlpflichtfächergruppe I Ssteme linerer Gleichungen mit zwei Vriblen lösen Qudrtische Gleichungen: Lösungsformel, edeutung der Diskriminnte, Koordinten der Schnittpunkte
Grundwissen m Ende der 9. Jhrgngsstufe Whlpflichtfächergruppe I Ssteme linerer Gleichungen mit zwei Vriblen lösen Qudrtische Gleichungen: Lösungsformel, edeutung der Diskriminnte, Koordinten der Schnittpunkte
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
F 0 =0, F 1 =1 und F n+1 =F n +F n-1 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
 F 0 0, F und F n+ F n +F n- 0,,,,,, 8,,, 4,, N A U T I L U S Fiboncci - Zhlen S. Nutilus - Nmen gebend für ds berühmte U-Boot des Kpitäns Nemo us Jules Vernes Romn "0 000 Meilen unter dem Meer" - ist ein
F 0 0, F und F n+ F n +F n- 0,,,,,, 8,,, 4,, N A U T I L U S Fiboncci - Zhlen S. Nutilus - Nmen gebend für ds berühmte U-Boot des Kpitäns Nemo us Jules Vernes Romn "0 000 Meilen unter dem Meer" - ist ein
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
360 2 r. 360 r2. α Bogenmaß. α 360. α 2π. 4 3 r3 V K. 4 r 2 O K
 Grundwissen Mthemtik 10. Klsse Kreis Länge eines Kreisbogens b 360 r r r b Fläche eines Kreissektors 360 r r r Bogenmß Bogenmß des Winkels : Umrechnungsformel: b α Bogenmß r α Bogenmß π α 360 Grdmß Kugel
Grundwissen Mthemtik 10. Klsse Kreis Länge eines Kreisbogens b 360 r r r b Fläche eines Kreissektors 360 r r r Bogenmß Bogenmß des Winkels : Umrechnungsformel: b α Bogenmß r α Bogenmß π α 360 Grdmß Kugel
Logarithmen zu speziellen und häufig gebrauchten Basen haben eigene Namen: Der Logarithmus zur Basis 10 heißt dekadischer oder Zehnerlogarithmus:
 0 Dr Andres M Seifert Sternstunden in Mthe, Physik und Technik wwwsternstunden-odenwldde Logrithmen Die Gleichung vom Typ b wird mit Hilfe des Logrithmus gelöst Der Logrithmus von zur Bsis b ist die Zhl,
0 Dr Andres M Seifert Sternstunden in Mthe, Physik und Technik wwwsternstunden-odenwldde Logrithmen Die Gleichung vom Typ b wird mit Hilfe des Logrithmus gelöst Der Logrithmus von zur Bsis b ist die Zhl,
Nutzung der Abwärme aus Erneuerbare-Energie-Anlagen
 5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
Seminar zum anorganisch-chemischen Praktikum. Quantitative Analyse. Patrick Schwarz
 Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004
 Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
Musterlösung zu Aufgabe 1 (Klassenstufe 9/10)
 Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
