Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt 5
|
|
|
- Bettina Voss
- vor 6 Jahren
- Abrufe
Transkript
1 Prof. J. Esprz Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Vielen Dnk n Jn Wgener für die erweiterten Aufgenlösungen Einführung in die theoretische Informtik Sommersemester 2017 Üungsltt 5 Üungsltt Wir unterscheiden zwischen Üungs- und Agelättern. Auf diesem Üungsltt finden Sie eine Üersicht üer die Kernspekte, die Sie in Klenderwoche 22 in den Tutorien diskutieren, üen und vertiefen. Die Aufgen uf diesem Bltt dienen dem Üen und Verstehen des Vorlesungsstoffes, sowie dem eigenständigen Erreiten der Kernspekte. Außerdem sollen Ihnen diese Aufgen uch helfen, ein Gefühl dfür zu ekommen, ws Sie inhltlich in der Klusur erwrtet. Klusurufgen können jedoch deutlich von den hier gestellten Aufgen weichen. Aschreien und Auswendiglernen von Lösungen wird Ihnen dher keinen duerhften Erfolg in der Vorlesung ringen. Frgen zu den Üungslättern können Sie montgs is donnerstgs von 12 Uhr is 14 Uhr in der THEO-Sprechstunde in Rum stellen. Kernspekte K5.1 korrektes Wiedergeen der folgenden Definitionen Myhill-Nerode-Reltion Äquivlenzklsse inäquivlente Zustände in einem DFA K5.2 zu einem gegeenen DFA den minimlen DFA ngeen K5.3 zu einem gegeenen Automten den Quotientenutomten ngeen K5.4 für reguläre Sprchen Sprchgleichheit mithilfe von Minimierung prüfen K5.5 mithilfe der Myhill-Nerode-Reltion eweisen zw. widerlegen, dss eine gegeene Sprche regulär ist AUFGABE 5.1. Geen Sie jeweils eine formle Sprchen üer dem Alphet Σ = {, } mit folgenden Eigenschften n: Stufe B () endlich () unendlich und regulär (c) nicht regulär und kontextfrei Beschreien Sie in eigenen Worten, wie Sie ei der Konstruktion der Sprchen vorgegngen sind, um sicher zu stellen, dss die Sprche die gewünschte Eigenschft ht. Erweiterte Lösungsskizze Sei Σ = {, }. Gi jeweils eine formle Sprche A üer Σ mit gegeenen Eigenschften n. () Eine endliche Sprche A = = Es ist lediglich druf zu chten, dss die Sprche nur endlich viele Wörter enthält. "Keine Wörterïst wohl die einfchste Art, ds sicherzustellen. () Eine unendliche, reguläre Sprche A = Σ = Die Sprche soll unendlich und regulär sein, d.h. sie muss durch einen regulären Ausdruck drstellr sein. Für Σ ist ds offensichtlich der Fll: ( ) Außerdem enthält Σ uch unendlich viele Wörter, z.b. lle der Form n, n N 0. (c) Eine nicht reguläre, kontextfreie Sprche A = { n n n N 0} = Diese Sprche ist eknntlich nicht regulär (leicht mit Pumping-Lemm für reguläre Sprchen zu zeigen). Allerdings ist sie kontextfrei, d es möglich ist, eine kontextfreie (Typ-2) Grmmtik zu konstruieren, die genu A erzeugt: Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 1/15
2 G = ({S}, Σ, P, S) mit P : S S ε AUFGABE 5.2. In der Vorlesung hen Sie ein Verfhren zur Minimierung von DFAs gesehen. Wir erweitern diesen Algorithmus, dmit er zusätzlich ds unterscheidende Wort w für ein Pr inäquivlenter Zuständen erechnet. () Erweitern Sie den Minimierungslgorithmus so, dss er für jedes Pr von inäquivlenten Zuständen q, p Q eines DFAs D = (Q, Σ, δ, q 0, F) ein kürzestes Wort w {q,p} mit δ(q, w {q,p} ) F δ(p, w {q,p} ) F erechnet. () Determinisieren und dnn minimieren Sie die folgenden NFAs. Verwenden Sie hierfür den erweiterten Minimierungslgorithmus us (). Bestimmen Sie hierei uch die Ahängigkeiten D[{p, q}] zwischen den Pren der Zustände gemäß dem Verfhren der Vorlesung. (i) NFA N 1 :,, Stufe C q 0 q 1 q 2 (ii) NFA N 2 : (iii) NFA N 3 : 1, 2, 4 3 Hinweise: Konstruieren Sie ei der Determinisierung nur die vom Strtzustnd erreichren Zustände. Wir verwenden ds Alphet Σ = {, }. Erweiterte Lösungsskizze () Erweitere den Minimierungslgorithmus us der Vorlesung, sodss er für ein Pr von nicht äquivlenten Zuständen p, q Q ein kürzestes Wort w erechnet, welches die eiden Zustände unterscheidet, d.h.: δ(p, w) F und δ(q, w) / F oder δ(p, w) / F und δ(q, w) F Idee: Trge eim Ausfüllen der Telle inäquivlenter Zustände sttt eines Kreuzes n der jeweiligen Stelle ein unterscheidendes Wort w ein. Flls einer der eiden Zustände ein Endzustnd ist und der ndere nicht, so ist ds kürzeste, die eiden unterscheidende Wort w = ε. Sonst können zwei Zustände p und q nur dnn unterschieden werden, wenn mn von ihnen us mit einem Zeichen Σ in ein ereits durch ein Wort v unterscheidres Zustndspr p und q gelngt. Dnn ist er w = v ein Wort, welches p und q unterscheidet. Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 2/15
3 () Determinisiere den jeweils gegeenen NFA und minimiere ihn dnn mit dem erweiterten Minimierungsverfhren us Teilufge (). I NFA N 1:,, q 0 q 1 q 2 Determinisieren mittels Potenzmengenkonstruktion liefert D 1: {q 0} {q 0, q 1} {q 0, q 2} {q 0, q 1, q 2} = Q Ausfüllen der Minimierungstelle liefert folgende Ergenisse: {q 0} {q 0, q 1} {q 0, q 2} Q {q 0} = {q 0, q 1} = - - {q 0, q 2} ε ε = - Q ε ε = Beim ersten Durchluf der Telle sind Pre von End- und Nicht-End- Zuständen zu mrkieren. Diese unterscheiden sich stets durch ds Wort ε. {q 0} {q 0, q 1} {q 0, q 2} Q {q 0} = {q 0, q 1} = - - {q 0, q 2} ε ε = - Q ε ε = Beim zweiten Durchluf können q 0,q 2 und q 0,q 1,q 2 nicht unterschieden werden. q 0 und q 0,q 1 führen llerdings mit dem Zeichen in ds Zustndspr q 0 und q 0,q 2. Diese eiden können ereits durch ε unterschieden werden, d.h. q 0 und q 0,q 1 können durch ε= unterschieden werden. Beim nächsten Durchlufen der Telle können keine weiteren Felder usgefüllt werden, d.h. lle noch nicht ls unterschiedlich mrkierten Zustndspre können ls äquivlent gekennzeichnet werden. Dmit können die eiden Zustände {q 0, q 2} und {q 0, q 1, q 2} zu einem Zustnd zusmmengefsst werden. Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 3/15
4 Ds ergit dnn den Minimierten DFA D m 1 :, {q 0} {q 0, q 1} {q 0, q 2}, Q II NFA N 2: Determinisieren mittels Potenzmengenkonstruktion liefert D 2: {0} {1, 2} {11, 22} {111, 222} Ausfüllen der Minimierungstelle liefert folgende Ergenisse: {0} {1, 2} {11, 22} {111, 222} {0} = {1, 2} ε = - - {11, 22} ε = - {111, 222} ε ε = Beim ersten Durchluf der Telle sind Pre von End- und Nicht-End- Zuständen zu mrkieren. Diese unterscheiden sich stets durch ds Wort ε. {0} {1, 2} {11, 22} {111, 222} {0} = {1, 2} ε = - - {11, 22} ε = - {111, 222} ε ε = Beim zweiten Durchluf können 0 und 111,222 nicht unterschieden werden. 1,2 und 11,22 führen llerdings mit dem Zeichen in ds Zustndspr 11,22 und 111,222. Diese eiden können ereits durch ε unterschieden werden, d.h. 1,2 und 11,22 können durch ε= unterschieden werden. Beim nächsten Durchlufen der Telle können keine weiteren Felder usgefüllt werden, d.h. lle noch nicht ls unterschiedlich mrkierten Zustndspre können ls äquivlent gekennzeichnet werden. Dmit können die eiden Zustände {0} und {111, 222} zu einem Zustnd zusmmengefsst werden. Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 4/15
5 Ds ergit dnn den Minimierten DFA D m 2 : {0}, {111, 222} {1, 2} {11, 22} III NFA N 3:, 2 1, 4 3 Determinisieren mittels Potenzmengenkonstruktion liefert D 3: {2, 3, 4} {1, 2, 3, 4} {2, 3} {1, 2, 3} {1} {1, 3, 4} {2} {3, 4} Ausfüllen der Minimierungstelle liefert folgende Ergenisse: {1} {2, 3} {2} {2, 3, 4} {1, 2, 3} {3, 4} {1, 2, 3, 4} {1, 3, 4} {1} = {2, 3} ε = {2} ε = {2, 3, 4} ε = {1, 2, 3} ε ε ε = {3, 4} ε ε = - - {1, 2, 3, 4} ε ε ε ε = - {1, 3, 4} ε ε ε ε = Beim ersten Durchlufen der Telle werden wie geht Pre von einem End- und einem Nicht- Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 5/15
6 End-Zustnd ls inäquivlent mrkiert. Ds jeweilige unterscheidende Wort ist ε. Beim zweiten Durchlufen der Telle erhält mn {1} {2, 3} {2} {2, 3, 4} {1, 2, 3} {3, 4} {1, 2, 3, 4} {1, 3, 4} {1} = {2, 3} ε = {2} ε = {2, 3, 4} ε = {1, 2, 3} ε ε ε = {3, 4} ε ε = - - {1, 2, 3, 4} ε ε ε ε = - {1, 3, 4} ε ε ε ε = {2} und {2, 3} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2, 3}, {1, 2, 3} kommt. Dieses ist ereits durch ε unterscheidr. Dher sind {2} und {2, 3} durch ε = unterscheidr. {2} und {2, 3, 4} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2, 3}, {1, 2, 3, 4} kommt. Dieses ist ereits durch ε unterscheidr. Dher sind {2} und {2, 3, 4} durch ε = unterscheidr. {1} und {1, 2, 3} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2}, {1, 2, 3} kommt. Dieses ist ereits durch ε unterscheidr. Dher sind {1} und {1, 2, 3} durch ε = unterscheidr. {2} und {3, 4} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2, 3}, {1, 3, 4} kommt. Dieses ist ereits durch ε unterscheidr. Dher sind {2} und {3, 4} durch ε = unterscheidr. {1} und {1, 2, 3, 4} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2}, {1, 2, 3, 4} kommt. Dieses ist ereits durch ε unterscheidr. Dher sind {1} und {1, 2, 3, 4} durch ε = unterscheidr. {1} und {1, 3, 4} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2}, {1, 2, 3, 4} kommt. Dieses ist ereits durch ε unterscheidr. Dher sind {1} und {1, 3, 4} durch ε = unterscheidr. Der dritte Durchluf der Telle ergit dnn {1} {2, 3} {2} {2, 3, 4} {1, 2, 3} {3, 4} {1, 2, 3, 4} {1, 3, 4} {1} = {2, 3} ε = {2} ε = {2, 3, 4} ε = {1, 2, 3} ε ε ε = {3, 4} ε ε = - - {1, 2, 3, 4} ε ε ε ε = - {1, 3, 4} ε ε ε ε = {2, 3} und {3, 4} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2}, {2, 3, 4} kommt. Dieses ist ereits durch unterscheidr. Dher sind {2, 3} und {3, 4} durch unterscheidr. {3, 4} und {2, 3, 4} sind unterscheidr, d mn von dort us mit einem in ds Zustndspr {2}, {2, 3, 4} kommt. Dieses ist ereits durch unterscheidr. Dher sind {3, 4} und {2, 3, 4} durch unterscheidr. Beim nächsten Durchlufen der Telle können keine weiteren Felder usgefüllt werden, d.h. lle noch nicht ls unterschiedlich mrkierten Zustndspre können ls äquivlent gekennzeichnet werden. Dmit können die eiden Zustände {2, 3} und {2, 3, 4} sowie die drei Zustände {1, 2, 3}, {1, 3, 4} und {1, 2, 3, 4} jeweils zu einem Zustnd zusmmengefsst werden. Ds ergit dnn den Minimierten DFA D m 3 : Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 6/15
7 {2, 3}, {2, 3, 4} {1, 2, 3}, {1, 3, 4}, {1, 2, 3, 4} {1} {3, 4} {2} AUFGABE 5.3. Sei L = L( c ) üer dem Alphet Σ = {,, c}. () Entscheiden Sie, welche der folgenden Äquivlenzen whr sind und egründen Sie Ihre Antwort: Stufe C ε? L? L c c? L c () Sei v = c. Geen Sie ein Wort u v n, so dss u L v. (c) Geen Sie die Mengen [] L, [c] L und [c] L n. (d) Geen Sie nun L, so dss c L, c L und L. Weiterhin soll ε, L gelten. Erweiterte Lösungsskizze Seien Σ = {,, c} und L = L( c ) Die Frge, o u? L v ist: Gilt für lle Wörter w Σ : uw L vw L? Anlog dzu ist Frge, o u? L v: Git es ein Wort w Σ, sodss zwr uw L er vw / L zw. sodss uw / L er vw L? Die Äquivlenzklsse eines Wortes v ist dnn: [v] L = {u Σ u L v} () Sind die folgenden Äquivlenzen korrekt? Wrum (nicht)? [v] L ist die Menge ller Wörter, die äquivlent zu v sind: Erste Frge: Welche Wörter w dürfen n v drngehängt werden, sodss vw noch in der Sprche L liegt? [v] L ist nicht die Menge dieser Wörter w, sondern die Menge der Wörter u n die noch genu die gleichen Wörter w ngehängt werden dürfen, nicht mehr und nicht weniger. ε? L Whr, d sowohl nch einem ε ls uch nch einem noch genu Wörter der Form c folgen dürfen. D.h. forml usgedrückt: ( w Σ. εw L w L w L( c ) = L ) Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 7/15
8 ? L c Flsch! Gegeneispiel ist w =. Es gilt zwr w = L, er cw = c / L. c? L c Flsch! Gegeneispiel ist w = ε. Es gilt zwr cw = c L, er cw = c / L. () v = c Gi ein Wort u n, sodss u v, er u L v. Welche Worte w drf mn noch n v nhängen, sodss uw L? = Keine! In v steht ereits ein vor einem, ws für kein Wort in L erlut ist: c Für welche Worte u gilt ds noch, dss mn nicht mehr in der Sprche liegen knn, egl welches Suffix w mn noch n u nhängt? = Alle, die ein, c oder c enthlten. Diese Zeichenkomintionen dürfen in keinem Wort in L uftuchen, d.h. wenn ein Wort u ereits mindestens eine der drei enthält, knn mn uch durch nhängen eines elieigen Suffixes nicht mehr in der Sprche lnden. Beispiel für ein solches Wort wäre u = c. (c) Gi lle Elemente der gegeenen Äquivlenzklssen n (z.b. ls regulären Ausdruck). [] L Welche Wörter w Σ dürfen n drngehängt werden, sodss w noch in L liegt? = s dürfen keine mehr ngehängt werden, d j ereits ein vorkm, d.h. nur noch Wörter der Form c dürfen ngehängt werden. L( c ) ist er nicht die gesuchte Menge. Die gesuchte Menge ist die Menge ller Wörter, n die uch noch genu Wörter us L( c ) ngehängt werden dürfen: = Wenn isher in einem Wort nur s vorkmen, so drf mn zwr Wörter der Form c nhängen, er uch eispielsweise ds Wort c. D.h. Wörter der Form sind nicht in der gesuchten Menge. Km in einem Wort hingegen schon ein c vor, so drf eispielsweise c nicht mehr ngehängt werden. Wir suchen lso gerde nch Wörtern, in denen elieig viele s und dnn mindestens ein vorkommt, er kein c: Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 8/15
9 [] L = L( ) [c] L Welche Wörter w Σ dürfen n c drngehängt werden, sodss c w noch in L liegt? = s und s dürfen keine mehr ngehängt werden, d j ereits ein c vorkm, d.h. nur noch Wörter der Form c dürfen ngehängt werden. L(c ) ist er nicht die gesuchte Menge. Die gesuchte Menge ist die Menge ller Wörter, n die uch noch genu Wörter us L(c ) ngehängt werden dürfen: = Wenn isher in einem Wort nur s und dnn s vorkmen, dnn dürfen zwr uch noch elieig viele c s ngehängt werden, er een noch mehr; z.b. nämlich uch c. D.h. Wörter der Form sind nicht äquivlent zu c. Wir suchen lso gerde nch den Wörtern, die (nch elieig vielen s und dnn s) mindestens ein c enthlten: [c] L = L( cc ) [c] L Welche Wörter w Σ dürfen n c drngehängt werden, sodss c w noch in L liegt? = Keine! Egl, ws mn n c noch nhängt, ds resultierende Wort wird immer die Zeichenkette c enthlten. Ds ist für Wörter in L nicht erlut. ist er nicht die gesuchte Menge. Die gesuchte Menge ist die Menge ller Wörter, n die uch nichts mehr ngehängt werden knn, um zu erreichen, dss ds resultierende Wort noch in der Sprche L liegt. = Ein Wort liegt genu dnn nicht in L, wenn es mindestens eine der drei Zeichenketten, c oder c enthält. Gdw. ein Wort u eine dieser drei ereits enthält, knn uch ein elieiger ngehängter Suffix w nicht mehr erreichen, dss ds resultierende Wort uw noch in L liegt. Schließlich enthält logischerweise uw die entsprechende Zeichenkette uch. Wir suchen lso gerde nch Wörtern, die eine der drei Zeichenketten, c oder c enthlten: ) [c] L = L (Σ ( c c) Σ = L In diesem Fll! Dss [w] L = L für w / Σ gilt ei Weitem nicht immer! Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 9/15
10 (d) Gi eine Sprche L n, für die folgende Bedigungen gilt: c L c L L ε L L Idee: Wie in der VL gesehen, korrespondieren die Äquivlenzklssen einer Sprche mit den Zuständen des minimlen DFAs für diese Sprche. Also könnte mn versuchen, einen DFA für L zu konstruieren und dei äquivlente Wörter in denselen Zustnd zu führen. Dnch knn mn die Sprche direkt vom DFA lesen. Erst einml sollen ε und in L liegen. Mn rucht lso Läufe für diese Wörter: Dnn soll noch L führen: sein, d.h. die eiden Wörter und können in denselen Zustnd Außerdem muss noch c L Wort : sein, d.h. ds Wort c sollte in den gleichen Zustnd führen, wie ds c Als letztes muss noch c L sein. Ds ist er in der Sprche des isherigen DFA ereits der Fll, d ds Wort c kzeptiert wird, während ds Wort nicht kzeptiert wird. Also c L und / L. Folglich knn L einfch vom Automten gelesen werden. D dieser nicht viele Wörter kzeptiert, können sie uch einfch ufgelistet werden: L = {ε, c,, } AUFGABE 5.4. Entscheiden Sie, o folgende Sprchen üer dem Alphet Σ = {,, c} regulär sind. Bestimmen Sie hierzu die Äquivlenzklssen der dzugehörigen Myhill-Nerode-Reltion. Flls die Sprche regulär ist, zählen Sie lle Äquivlenzklssen uf und zeichnen Sie den knonischen Minimlutomt M L = (Σ / L, Σ, δ L, [ε] L, F L ). Flls Stufe D Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 10/15
11 die Sprche nicht regulär ist, reicht es eine unendliche Menge von Äquivlenzklssen zu estimmen. () L 1 = { 2i i N 0 } () L 2 = { i i c i i N 0 } (c) L 3 = {w Σ w = 2 w } (d) L 4 = L(( ( c)) ) (e) L 5 = {wcw w {, } } Erweiterte Lösungsskizze Sei Σ = {,, c}. Prüfe mithilfe der Äquivlenzklssen der gegeenen Sprchen, o diese regulär sind. Wenn es nur endlich viele Äquivlenzklssen git, so ist die Sprche regulär. Wenn mn llerdings unendlich viele inäquivlente Wörter finden knn, so ist die Sprche nicht regulär (, d dnn der minimle Automt unendlich viele Zustände hen müsste). () L 1 = { 2i i N 0} Sprche ller Wörter gerder Länge, die nur us s estehen. Die Äquivlenzklssen zu estimmen geht hier wohl m einfchsten direkt üer den minimlen DFA, der die Sprche L 1 kzeptiert. Dieser ist so zu konstruieren: [ε] L1 [] L1,c,c [] L1,,c Jeder Zustnd steht für eine Äquivlenzklsse. Eine Äquivlenzklsse wird mit einem Wort ezeichnet, dss in der Klsse liegt (egl welches), d.h. mit einem Wort, ds in den entsprechenden Zustnd führt. Die Menge ller Wörter, die in der Äquivlenzklsse eines Zustndes liegen, sind dnn lle Wörter, die in den jeweiligen Zustnd führen: ) [ε] L1 = L (() Alle Wörter, die in den linken oeren Zustnd führen, sind Wörter gerder Länge, die nur us s estehen. ) [] L1 = L (() ) [] L1 = L (Σ ( c) Σ Alle Wörter, die in den rechten oeren Zustnd führen, sind Wörter ungerder Länge, die nur us s estehen. Alle Wörter, die in den unteren Zustnd führen, sind Wörter, die mindestens ein oder c enthlten. () L 2 = { i i c i i N 0} Diese Sprche ist eknntlich nicht regulär. Um ds zu zeigen, reicht es, eine unendliche Fmilie von Wörtern u (0), u (1), u (2)... nzugeen, die prweise nicht äquivlent sind, d.h. für lle i, j mit i j gilt: u (i) L2 u (j) Beispiel für eine derrtige Fmilie von Wörtern ist ε,,,,..., lso u (i) = i. Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 11/15
12 Beweis: Seien i, j N 0 und i j: = i i c i L 2 er j i c i / L 2 = i L2 j, unhängig dvon, ws i und j sind. Ds heißt er wiederum, dss [ i ] L2 [ j ] L2. Also ht die Sprche L 2 unendlich viele Äquivlenzklssen und ist dmit nicht regulär. (c) L 3 = {w Σ w = 2 w } Sprche ller Wörter, die doppelt so viele s wie s enthlten. Diese Sprche ist eenflls nicht regulär. Um ds zu zeigen, reicht es, eine unendliche Fmilie von Wörtern u (0), u (1), u (2)... nzugeen, die prweise nicht äquivlenz sind, d.h. für lle i, j mit i j gilt: u (i) L2 u (j) Beispiel für eine derrtige Fmilie von Wörtern ist ε,,,,..., lso u (i) = i. Beweis: Seien i, j N 0 und i j: = i 2i L 3 er j 2i / L 3 = i L3 j, unhängig dvon, ws i und j sind. Ds heißt er wiederum, dss [ i ] L3 [ j ] L3. Also ht die Sprche L 3 unendlich viele Äquivlenzklssen und ist dmit nicht regulär. (d) L 4 = L( ( ( c) ) ) Sprche ller Wörter, die uf oder c enden. Betrchtet mn diese Sprche, so git es eigentlich nur zwei Fälle, die zu unterscheiden sind: Ds isherige Wort endet uf zw. ds isherige Wort endet uf oder c (oder ist ds leere Wort). Wenn ein Wort v uf oder uf c endet, dnn liegt es in der Sprche. D.h. mn knn ε ls Suffix nhängen und ds entstndene Wort vε liegt immer noch in der Sprche. Außerdem knn mn, d es j in L 4 nur um ds letzte Zeichen geht, jedes elieige Wort w L 4 n v drnhängen und vw wird in L 4 liegen. Wenn ein Wort v er uf endet, so knn mn uch ein elieiges Wort w L 4 und vw wird in L 4 liegen. Nur mit w = ε geht ds jetzt nicht mehr. n v drnhängen Drus folgt, dss es exkt zwei Äquivlenzklssen git: [ε] L4 = L 4 Alle Wörter in L 4 sind in einer Äquivlenzklsse, d mn n diese noch genu ε oder ein uf oder c endendes Wort hängen drf. [] L4 = L 4{} + = Σ \ L 4 Alle Wörter ußerhl L 4 sind in einer Äquivlenzklsse, d mn n diese noch genu ein uf oder c endendes Wort hängen drf. Der knonische Minimlutomt ht dnn entsprechend einen Zustnd für jede Äquivlenzklsse:,c [ε] L1 [] L1,c Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 12/15
13 (e) L 5 = {wcw w {, } } Diese Sprche ist nicht regulär. Um ds zu zeigen, reicht es, eine unendliche Fmilie von Wörtern u (0), u (1), u (2)... nzugeen, die prweise nicht äquivlenz sind, d.h. für lle i, j mit i j gilt: u (i) L5 u (j) Beispiel für eine derrtige Fmilie von Wörtern ist wieder ε,,,,..., lso u (i) = i. Beweis: Seien i, j N 0 und i j: = i c i L 5 er j c i / L 5 = i L5 j, unhängig dvon, ws i und j sind. Ds heißt er wiederum, dss [ i ] L5 [ j ] L5. Also ht die Sprche L 5 unendlich viele Äquivlenzklssen und ist dmit nicht regulär. Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 13/15
14 Definition (Monoid) Ein Monoid M,, 1 esteht us einer (Träger-)Menge M, einer ssozitiven Aildung : M M M und einem zgl. neutrlen Element 1 M (d.h. m M. m 1 = m = 1 m). Ist kommuttiv, dnn wird M,, 1 ls kommuttives Monoid ezeichnet. Gilt m M. m m = m, so wird M,, 1 ls idempotentes Monoid ezeichnet. Definition (Kleene Alger) Eine Kleene Alger K, +,,, 0, 1 esteht us einer Trägermenge K, den inären Opertionen +: K K K (Addition), : K K K (Multipliktion), der unären Opertion : K K (Stern) und zwei Konstnten 0, 1 K. Mittels der Addition definiert mn die inäre Reltion uf K durch Def + = Wie ülich schreit mn kurz für. Um Klmmern zu spren, gilt Stern vor Punkt vor Strich. Eine Kleene Alger erfüllt folgende Eigenschften für lle,, c, x K: Ax1: K, +, 0 ist ein kommuttives und idempotentes Monoid. Ax2: K,, 1 ist ein Monoid. Ax3: ( + c) = + c und ( + )c = c + c. Ax4: 0 = 0 = 0. Ax5: 1 + und 1 +. Ax6: + x x x und + x x x. AUFGABE 5.5. In dieser Aufge strhieren wir von der konkreten Interprettion von regulären Ausdrücken ls Konstruktionseschreiungen regulärer Sprchen. Ziel ist es den Zusmmenhng mit Pfdprolemen im Bereich der Informtik und dem Lösen linerer Gleichungssysteme zu verdeutlichen. () Sei Σ ein Alphet. Beweisen Sie, dss 2 Σ,,,,, {ε} eine Kleene Alger ist für LL := L L := {ww w L, w L } und L := k N 0 L k Stufe E () Die Addition und ds Minimum uf R seien uf [, ] = R {± } wie folgt erweitert: Weiterhin gelte: + = + = + = min(, ) = min(, ) = min(, ) = := { flls [, 0) 0 flls [0, ] Beweisen Sie, dss R {± }, min, +,,, 0 eine Kleene Alger ist. (c) Zeigen Sie, dss in jeder Kleene Alger K, +,,, 0, 1 für elieige,, c, d, e, f K gilt: (i) ist eine prtielle Ordnung uf K, die monoton zgl. Addition, Multipliktion und Stern ist, d.h.: (c c c c + c + c ) (ii) ist die zgl. kleinste Lösung der lineren Ungleichung + X X in K (X Vrile), genuer: + ( ) x K : + x x x Entsprechend ist die kleinste Lösung in K von + X X. Mn knn zeigen, dss jedes linere Ungleichungssystem 1,1X 1 + 1,2X ,nX n + 1 X 1. n,1x 1 + n,2x n,nx n + n X n mit i,j, i K und X 1,..., X n Vrilen stets eine eindeutige -kleinste Lösung in K ht, d.h. dss es konkrete Elemente x 1,..., x n K git, so dss für X 1 = x 1,..., X n = x n lle oigen Ungleichungen erfüllt sind, und für Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 14/15
15 jede weitere Lösung X 1 = y 1,..., X n = y n K stets x i y i gilt. Insesondere gilt x 1 = 1,1( 1,2x ,nx n + 1) Somit knn ds Guß-Verfhren zur Bestimmung von x 1,..., x n verwendet werden. (d) Bestimmen Sie die kleinste Lösung x 1, x 2, x 3, x 4 für folgendes System: X + Y + ez X cx + dy + fz Y 1 Z (e) Bestimmen Sie den regulären Ausdruck für den Zustnd X. Durch welche Werte muss mn,, c, d, e, f konkret ersetzen, dmit sich die in (d) erechneten Terme in 2 Σ,,,,, {ε} zu dem gewünschten Ausdruck uswertet? X d c d Y Z (f) Bestimmen Sie die Länge eines kürzesten Pfdes von jedem Knoten zum Knoten Z in folgendem gewichteten Grphen. Durch welche Werte muss mn,, c, d, e, f konkret ersetzen, dmit sich die in (d) erechneten Terme in R {± }, min, +,, 0 zu den gesuchten Pfdlängen uswerten? X Y Z Bei Frgen oder Prolemen schreien Sie eine Mil n theo-ueungsleitung@in.tum.de! 15/15
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Teil V: Formale Sprachen
 Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Inhaltsverzeichnis. Inhaltsverzeichnis... 1 3.Logik... 2. 3.1 Zahlensysteme... 2. 3.2 Grundbegriffe zweiwertiger Logik... 13
 Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Reguläre Sprachen und endliche Automaten
 2 Reguläre Sprchen und endliche Automten Sei Σ = {, b,...} ein endliches Alphbet. Ein endliches Wort über Σ ist eine Folge w = 0... n 1, wobei i Σ für i = 0,...,n 1. Wir schreiben w für die Länge von w,
2 Reguläre Sprchen und endliche Automten Sei Σ = {, b,...} ein endliches Alphbet. Ein endliches Wort über Σ ist eine Folge w = 0... n 1, wobei i Σ für i = 0,...,n 1. Wir schreiben w für die Länge von w,
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Karlsruher Institut für Technologie
 Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
Identifizierbarkeit von Sprachen
 FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
Seminar Quantum Computation - Finite Quanten-Automaten und Quanten-Turingmaschinen
 Seminr Quntum Computtion - Finite Qunten-Automten und Qunten-Turingmschinen Sebstin Scholz sscholz@informtik.tu-cottbus.de Dezember 3. Einleitung Aus der klssischen Berechenbrkeitstheorie sind die odelle
Seminr Quntum Computtion - Finite Qunten-Automten und Qunten-Turingmschinen Sebstin Scholz sscholz@informtik.tu-cottbus.de Dezember 3. Einleitung Aus der klssischen Berechenbrkeitstheorie sind die odelle
Definition Suffixbaum
 Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
Suffix-Bäume Definition Suche nch einer Menge von Mustern Längste gemeinsme Zeichenkette Pltzreduktion Suffixbäume für Muster Alle Pre Suffix-Präfix Übereinstimmung Sich wiederholende Strukturen Definition
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit bietet, ihre statistischen Meldungen über das Internet auszufüllen und einzureichen.
 Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Endliche Automaten. Prof. Dr. W. Vogler. Sommersemester 2007
 Endliche Automten Prof. Dr. W. Vogler Sommersemester 2007 1 INHALTSVERZEICHNIS i Inhltsverzeichnis 1 Wörter und Monoide 1 2 Endliche Automten 4 3 Anwendung: Diophntische Gleichungen 9 4 Minimierung endlicher
Endliche Automten Prof. Dr. W. Vogler Sommersemester 2007 1 INHALTSVERZEICHNIS i Inhltsverzeichnis 1 Wörter und Monoide 1 2 Endliche Automten 4 3 Anwendung: Diophntische Gleichungen 9 4 Minimierung endlicher
5.3 Dynamisches Sitzen und Stehen
 Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
FernUniversität Gesamthochschule in Hagen
 FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
 S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
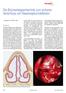 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Einschub: Zahlendarstellung und Codes
 Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
Einführung in die Schaltalgebra
 Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Public-Key-Verfahren: Diffie-Hellmann und ElGamal
 Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Seminar zum anorganisch-chemischen Praktikum. Quantitative Analyse. Patrick Schwarz
 Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil I: Theorie. Michael Buhlmann
 Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Programmieren in C/C++ und Matlab
 Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Progrmmieren in C/C und Mtl Sine Schmidt & Sestin Buer Institut für Geowissenschften Christin-Alrechts-Universität zu Kiel Progrmmieren in C/C und Mtl CAU, SS 08 for- / while-schleifen: - numerische Integrlerechnung
Kapitel 8 Apps installieren und verwalten
 Kpitel 8 Apps instllieren und verwlten In diesem Kpitel sehen wir uns die Stndrdquelle ller Apps einml etws genuer n, den Google Ply Store (kurz: Google Ply oder Ply Store). Er ist der Dreh- und Angelpunkt,
Kpitel 8 Apps instllieren und verwlten In diesem Kpitel sehen wir uns die Stndrdquelle ller Apps einml etws genuer n, den Google Ply Store (kurz: Google Ply oder Ply Store). Er ist der Dreh- und Angelpunkt,
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
START DEUTSCH 1. Übungssatz 02. Goethe-Institut 2008. ISBN 3-936753-31-8 Übungsheft ISBN 3-936753-32-6 Tonkassette ISBN 3-936753-33-4 CD
 in puncto Bonn 04_08_08 SD1_Ü02_04 START DEUTSCH 1 Goethe-Institut 2008 ISBN 3-936753-31-8 Üungsheft ISBN 3-936753-32-6 Tonkssette ISBN 3-936753-33-4 CD Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen, Schreien
in puncto Bonn 04_08_08 SD1_Ü02_04 START DEUTSCH 1 Goethe-Institut 2008 ISBN 3-936753-31-8 Üungsheft ISBN 3-936753-32-6 Tonkssette ISBN 3-936753-33-4 CD Inhlt Vorwort 3 Kndidtenlätter Hören 5 Lesen, Schreien
1KOhm + - y = x LED leuchtet wenn Schalter x gedrückt ist
 . Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
. Ohm = LED leuchtet wenn chlter gedrückt ist 2. Ohm = NICH ( = NO ) LED leuchtet wenn chlter nicht gedrückt ist = ist die Negtion von? Gibt es so einen kleinen chlter (Mikrotster)? 2. Ohm = UND LED leuchtet
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
Hinweise für den schulischen Umgang mit lese-/rechtschreibschwachen Kindern speziell in der Sekundarstufe I
 Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Schritte international im Beruf
 1 Ws mchen die Leute uf dem Foto? Kreuzen Sie n. Die Leute sind ei der Berufsertung. mchen zusmmen ein Seminr. hen gerde Puse. pnthermedi / Werner H. Wer sind die Leute? Ergänzen Sie. die Referentin /
1 Ws mchen die Leute uf dem Foto? Kreuzen Sie n. Die Leute sind ei der Berufsertung. mchen zusmmen ein Seminr. hen gerde Puse. pnthermedi / Werner H. Wer sind die Leute? Ergänzen Sie. die Referentin /
Übungsblatt Gleichungssysteme Klasse 8
 Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Boole'sche Algebra. Inhaltsübersicht. Binäre Funktionen, Boole'sche Algebren, Schaltalgebra. Verknüpfungen der mathematischen Logik
 Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
Boole'sche Algebr Binäre Funktionen, Boole'sche Algebren, Schltlgebr Inhltsübersicht Verknüpfungen der mthemtischen Logik Boole sche Algebren Grundelemente der Schltlgebr Regeln der Schltlgebr Normlformen
QualitŠtskriterien fÿr die betriebliche Gesundheitsfšrderung
 WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
5.4 CMOS Schaltungen und VLSIDesign
 Kp5.fm Seite 447 Dienstg, 7. Septemer 2 :55 3 5.4 CMOS Schltungen und VLSI Design 447 r u u r id + + A. 5.39: Progrmmierrer Gitterustein 5.4 CMOS Schltungen und VLSIDesign Die Boolesche Alger eginnt mit
Kp5.fm Seite 447 Dienstg, 7. Septemer 2 :55 3 5.4 CMOS Schltungen und VLSI Design 447 r u u r id + + A. 5.39: Progrmmierrer Gitterustein 5.4 CMOS Schltungen und VLSIDesign Die Boolesche Alger eginnt mit
Gerd Wöstenkühler. Grundlagen der Digitaltechnik Elementare Komponenten, Funktionen und Steuerungen
 Gerd Wöstenkühler Grundlgen der Digitltehnik Elementre Komponenten, Funktionen und Steuerungen Inhlt 1 Einleitung... 11 1.1 Anloge unddigitledrstellungsformen... 11 1.1.1 AnlogeGrößendrstellung... 11 1.1.2
Gerd Wöstenkühler Grundlgen der Digitltehnik Elementre Komponenten, Funktionen und Steuerungen Inhlt 1 Einleitung... 11 1.1 Anloge unddigitledrstellungsformen... 11 1.1.1 AnlogeGrößendrstellung... 11 1.1.2
Matrizen und Determinanten
 Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Motivation. Kap. 4.2 Binäre Suchbäume ff Kap. 4.3: AVL-Bäume. Überblick. Pseudocode von SEARCH. in binären Suchbäumen. in binären Suchbäumen
 Kp. 4.2 inäre Schäme ff Kp. 4.: VL-äme Professor r. Lehrsthl für lgorithm Engineering, LS11 Fkltät für Informtik, TU ortmnd Motition Wrm soll ich hete hier leien? lncierte äme rchen Sie immer wieder! Ws
Kp. 4.2 inäre Schäme ff Kp. 4.: VL-äme Professor r. Lehrsthl für lgorithm Engineering, LS11 Fkltät für Informtik, TU ortmnd Motition Wrm soll ich hete hier leien? lncierte äme rchen Sie immer wieder! Ws
Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
 Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Institut für Volkswirtschaftslehre und Wirtschaftspolitik. Prof. Dr. Andreas Thiemer. VWL-Semesterprojekt Nr. 4 WS 2007/2008. Bayessche Lemminge
 Institut für Volkswirtschftslehre und Wirtschftspolitik Prof. Dr. ndres Thiemer VWL-Semesterprojekt Nr. 4 WS 007/008 yessche Lemminge Ein Experiment mit Informtionskskden Unter Mitreit von: Olg eder xel
Institut für Volkswirtschftslehre und Wirtschftspolitik Prof. Dr. ndres Thiemer VWL-Semesterprojekt Nr. 4 WS 007/008 yessche Lemminge Ein Experiment mit Informtionskskden Unter Mitreit von: Olg eder xel
Erweitern. a b. bd + bc. bd = ad+bc. bei ganzzahligem Nenner: Hauptnenner (= kgv der Nenner), z.b. 4 6 + 3 4 = 8 12 + 9. a d = ac
 F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
bei Problemen die Theorie und die Beispiele am Anfang jeder Lerneinheit durcharbeiten
 Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Eufic Guide Enfant ALL 14/12/04 15:44 Page 1 10 Tipps für Kids Spiel mit uns! Zur gesundenernährung
 Kids Ernährung für Tipps 10 Spiel mit uns! gesunden Zur Weißt du noch, wie du Rd fhren lerntest? Ds Wichtigste dei wr zu lernen ds Gleichgewicht zu hlten. Sold es gefunden wr, konntest du die Pedle gleichmäßig
Kids Ernährung für Tipps 10 Spiel mit uns! gesunden Zur Weißt du noch, wie du Rd fhren lerntest? Ds Wichtigste dei wr zu lernen ds Gleichgewicht zu hlten. Sold es gefunden wr, konntest du die Pedle gleichmäßig
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
über der Strangbreite 2. Zugleich vermindert Einschlüssen, wodurch sich die Qualität des gegossenen Stahls verbessert.
 S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
Grundwissen Abitur Analysis
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
Analysis I/II. Skript zur Vorlesung 2009/2010. Peter Junghanns
 Skript zur Vorlesung Anlysis I/II 9/ Peter Junghnns Hinweis: Ds vorliegende Skript stellt nur ein Gerüst zu den Inhlten der Vorlesung dr. Die Vorlesung selbst bietet weiterführende Erläuterungen, Beweise
Skript zur Vorlesung Anlysis I/II 9/ Peter Junghnns Hinweis: Ds vorliegende Skript stellt nur ein Gerüst zu den Inhlten der Vorlesung dr. Die Vorlesung selbst bietet weiterführende Erläuterungen, Beweise
Ntoneni-be Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen
 FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
Elemente der Analysis II: Zusammenfassung der wichtigsten Definitionen und Ergebnisse
 Elemente der Anlysis II: Zusmmenfssung der wichtigsten Definitionen und Ergebnisse J. Wengenroth Dies ist die einzige zugelssene Formelsmmlung, die bei der Klusur benutzt werden drf. Es dürfen Unterstreichungen
Elemente der Anlysis II: Zusmmenfssung der wichtigsten Definitionen und Ergebnisse J. Wengenroth Dies ist die einzige zugelssene Formelsmmlung, die bei der Klusur benutzt werden drf. Es dürfen Unterstreichungen
Kapitel 6 E-Mails senden und empfangen
 Kpitel 6 E-Mils senden und empfngen Sie ist zwr mittlerweile infolge des hohen Spmufkommens ein wenig in Verruf gerten, gehört er immer noch zum Stndrdkommuniktionsmittel des Weürgers: die E-Mil. Zentrle
Kpitel 6 E-Mils senden und empfngen Sie ist zwr mittlerweile infolge des hohen Spmufkommens ein wenig in Verruf gerten, gehört er immer noch zum Stndrdkommuniktionsmittel des Weürgers: die E-Mil. Zentrle
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Analysis I im SS 2011 Kurzskript
 Anlysis I im SS 2011 Kurzskript Prof. Dr. C. Löh Sommersemester 2011 Inhltsverzeichnis -2 Literturhinweise 2-1 Einführung 4 0 Grundlgen: Logik und Mengenlehre 5 1 Zählen, Zhlen, ngeordnete Körper 14 2
Anlysis I im SS 2011 Kurzskript Prof. Dr. C. Löh Sommersemester 2011 Inhltsverzeichnis -2 Literturhinweise 2-1 Einführung 4 0 Grundlgen: Logik und Mengenlehre 5 1 Zählen, Zhlen, ngeordnete Körper 14 2
Analysis 2. Mitschrift von www.kuertz.name
 Anlysis 2 Mitschrift von www.kuertz.nme Hinweis: Dies ist kein offizielles Script, sondern nur eine privte Mitschrift. Die Mitschriften sind teweilse unvollständig, flsch oder inktuell, d sie us dem Zeitrum
Anlysis 2 Mitschrift von www.kuertz.nme Hinweis: Dies ist kein offizielles Script, sondern nur eine privte Mitschrift. Die Mitschriften sind teweilse unvollständig, flsch oder inktuell, d sie us dem Zeitrum
17 Doppelbündel-Rekonstruktion mit Semitendinosussehne
 Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Personal und Finanzen der öffentlich bestimmten Fonds, Einrichtungen, Betriebe und Unternehmen (FEU) in privater Rechtsform im Jahr 2003
 Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
In Fachwerken gibt es demnach nur konstante Normalkräfte. Die Fachwerksknoten sind zentrale Kraftsysteme.
 Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Farbstichige Porträts: 30 PhotograPhie
 Frstichige Porträts: Erfhrungsgemäß sind Porträts die kritischsten Motive in einem Fotouch. Während die meisten Ntur- oder Architekturufnhmen eine zu strke Sättigung oder einen leichten Frstich vertrgen,
Frstichige Porträts: Erfhrungsgemäß sind Porträts die kritischsten Motive in einem Fotouch. Während die meisten Ntur- oder Architekturufnhmen eine zu strke Sättigung oder einen leichten Frstich vertrgen,
Therapiebegleiter Kopfschmerztagebuch
 Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
www. line21 Kommunikation Daten- und Telefontechnik über 1 Kabel mit 4 Adern. Kein Problem mit line21 natürlich von Rutenbeck!
 Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Beispiel-Abiturprüfung
 Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Die quadratische Gleichung und die quadratische Funktion
 Die quadratische Gleichung und die quadratische Funktion 1. Lösen einer quadratischen Gleichung Quadratische Gleichungen heißen alle Gleichungen der Form a x x c = 0, woei a,, c als Parameter elieige reelle
Die quadratische Gleichung und die quadratische Funktion 1. Lösen einer quadratischen Gleichung Quadratische Gleichungen heißen alle Gleichungen der Form a x x c = 0, woei a,, c als Parameter elieige reelle
Logische Grundschaltungen
 Elektrotechnisches Grundlgen-Lor II Logische Grundschltungen Versuch Nr. 9 Erforderliche Geräte Anzhl Bezeichnung, Dten GL-Nr. 1 Voltmeter 335 1 Steckrett SB 1 1 Steckrett SB 2 mit 5V Netzteil 1 Steckrett
Elektrotechnisches Grundlgen-Lor II Logische Grundschltungen Versuch Nr. 9 Erforderliche Geräte Anzhl Bezeichnung, Dten GL-Nr. 1 Voltmeter 335 1 Steckrett SB 1 1 Steckrett SB 2 mit 5V Netzteil 1 Steckrett
Technische Informatik 2
 TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
Endliche Automaten. S. Kuske: Endliche Automaten; 6.Novenber 2006
 1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
1 Endliche Automten Einfches Modellierungswekzeug (z.b. UML-Sttechrts) Verrbeiten Wörter/Ereignisfolgen Erkennen Sprchen Erluben schnelle Sprcherkennung Anwendungsbereiche: Objektorientierte Modellierung,
Brückenkurs Mathematik
 Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Analysis I/II - Vorlesungs-Script
 Anlysis I/II - Vorlesungs-Script Prof. Michel Struwe 05/06 Mitschrift: Eveline Hrdmeier Grphics: Prisc Greminger Mthis Weylnd Corrections: Prisc Greminger $Id: nlysis.tex 1237/1502 2006-10-19 21:13:30
Anlysis I/II - Vorlesungs-Script Prof. Michel Struwe 05/06 Mitschrift: Eveline Hrdmeier Grphics: Prisc Greminger Mthis Weylnd Corrections: Prisc Greminger $Id: nlysis.tex 1237/1502 2006-10-19 21:13:30
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
16 A. Was für eine Idee! A1 Verrückte Rekorde. a Ordne die Wortgruppen den Fotos zu. Welche Wörter kannst du auf den Fotos zeigen?
 16 A Ws für eine Idee! A1 Verrückte Rekorde Ordne die Wortgruppen den Fotos zu. Welche Wörter knnst du uf den Fotos zeigen? 1 prktisch, Hre, Friseur 2 singen, Sänger, Rockkonzert 3 wiegen, Tonne (= 1000
16 A Ws für eine Idee! A1 Verrückte Rekorde Ordne die Wortgruppen den Fotos zu. Welche Wörter knnst du uf den Fotos zeigen? 1 prktisch, Hre, Friseur 2 singen, Sänger, Rockkonzert 3 wiegen, Tonne (= 1000
Wie erfahre ich, welches Programm ich verwenden muss? 1. Wie kann ich meine Videobänder auf eine Disc übertragen? 5
 hp dvd writer Wie... Inhlt Wie erfhre ich, welches Progrmm ich verwenden muss? 1 Deutsch Wie knn ich eine Disc kopieren? 2 Wie knn ich meine änder uf eine Disc üertrgen? 5 Wie knn ich einen DVD-Film erstellen?
hp dvd writer Wie... Inhlt Wie erfhre ich, welches Progrmm ich verwenden muss? 1 Deutsch Wie knn ich eine Disc kopieren? 2 Wie knn ich meine änder uf eine Disc üertrgen? 5 Wie knn ich einen DVD-Film erstellen?
Installations und Bedienungsanleitung
 Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
Instlltions und Bedienungsnleitung EKRUCBS Instlltions und Bedienungsnleitung Deutsch Inhltsverzeichnis Inhltsverzeichnis Für den Benutzer 2 1 Schltflächen 2 2 Sttussymole 2 Für den Instllteur 3 3 Üersicht:
7. Portfolioinvestitionen und Wechselkursschwankungen. Literatur. Prof. Dr. Johann Graf Lambsdorff Universität Passau SS 2008
 Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
c dl SPiC (Teil C, SS 11) 13 Zeiger und Felder 13.1 Zeiger Einführung 13 1 Zeigervariable := Behälter für Verweise ( Adresse) Beispiel int x = 5;
 Überblick: Teil C Systemnhe Softwreentwicklung Einordnung: Zeiger (Pointer) Literl: Drstellung eines Wertes 0110 0001 12 Progrmmstruktur und Module Vrible: Bezeichnung chr ; eines Dtenobjekts Behälter
Überblick: Teil C Systemnhe Softwreentwicklung Einordnung: Zeiger (Pointer) Literl: Drstellung eines Wertes 0110 0001 12 Progrmmstruktur und Module Vrible: Bezeichnung chr ; eines Dtenobjekts Behälter
Vorlesungsskript Mathematik I für Wirtschaftsingenieure
 Vorlesungsskript Mthemtik I für Wirtschftsingenieure Verfsserin: HSD Dr. Sybille Hndrock TU Chemnitz Fkultät für Mthemtik e-mil: hndrock@mthemtik.tu-chemnitz.de Wintersemester 2005/06 Litertur [] Dllmnn,
Vorlesungsskript Mthemtik I für Wirtschftsingenieure Verfsserin: HSD Dr. Sybille Hndrock TU Chemnitz Fkultät für Mthemtik e-mil: hndrock@mthemtik.tu-chemnitz.de Wintersemester 2005/06 Litertur [] Dllmnn,
Analysis I Probeklausur 2
 WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
2008-06-11 Klassenarbeit 5 Klasse 10c Mathematik
 2008-06- Klssenrbeit 5 Klsse 0c Mtemtik Lösung Version 2008-06-4 Cindy t 3000 geerbt. ) Den Betrg will sie so nlegen, dss sie in 20 Jren doppelt so viel Geld t. Berecne, zu welcem Zinsstz sie ds Geld nlegen
2008-06- Klssenrbeit 5 Klsse 0c Mtemtik Lösung Version 2008-06-4 Cindy t 3000 geerbt. ) Den Betrg will sie so nlegen, dss sie in 20 Jren doppelt so viel Geld t. Berecne, zu welcem Zinsstz sie ds Geld nlegen
Werben auf askenrico
 Weren uf skenrico skenrico Ihr Online-Reiseführer für Mitteleurop Unser Online-Reiseführer ht eine rsnte Entwicklung zu verzeichnen. Gegründet Ende 2009, zählt er mit üer 10.000 montlichen Besuchern Mitte
Weren uf skenrico skenrico Ihr Online-Reiseführer für Mitteleurop Unser Online-Reiseführer ht eine rsnte Entwicklung zu verzeichnen. Gegründet Ende 2009, zählt er mit üer 10.000 montlichen Besuchern Mitte
Internationale Ökonomie I Vorlesung 3: Das Riccardo-Modell: Komparative Vorteile und Produktivität (Master)
 Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
Schützen Sie diejenigen, die Ihnen am Herzen liegen. Risikopremium
 Schützen Sie diejenigen, die Ihnen m Herzen liegen Risikopremium Verntwortung heißt, weiter zu denken Die richtige Berufswhl, die Gründung einer eigenen Fmilie, die eigenen vier Wände, der Schritt in die
Schützen Sie diejenigen, die Ihnen m Herzen liegen Risikopremium Verntwortung heißt, weiter zu denken Die richtige Berufswhl, die Gründung einer eigenen Fmilie, die eigenen vier Wände, der Schritt in die
Musterlösung zu Aufgabe 1 (Klassenstufe 9/10)
 Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
( 3) k ) = 3) k 2 3 für k gerade
 Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3
Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3
