1. Runde Aufgaben und Lösungen. Bundeswettbewerb Mathematik
|
|
|
- Kristian Beyer
- vor 6 Jahren
- Abrufe
Transkript
1 Budeswettewer Mthemtik Wisseshftszetrum Postfh 0 8 Bo Fo: Fx: e-mil: ifo@udeswettewer-mthemtik.de Korrekturkommissio Krl Fegert Aufge ud Lösuge. Rude 00 Üer Kommetre ud Ergäzuge zu diese Lösugseispiele freue wir us! Ashrift oder Emil Adresse s.o. Std: Mi 00
2 BWM 00 I Lösugseispiele Aufge : Zu Begi eies Spiels stehe der Tfel die Zhle,,..., 00. Ei Spielzug esteht drus, dss m eie elieige Azhl der Zhle der Tfel uswählt, de Elferrest der Summe dieser Zhle erehet ud die Tfel shreit, die usgewählte Zhle lösht. Bei eiem solhe Spiel stde irgedw oh zwei Zhle der Tfel. Eie dvo wr 000; m estimme die dere Zhl. Ergeis: I jedem Fll steht oh die Zhl der Tfel.. Beweis: Wir üerlege, wie sih die Gesmtsumme G ller Zhle der Tfel ei eiem Spielzug verädert: Die Summe der usgewählte Zhle ezeihe wir mit S, ihre Elferrest mit E. D ist G eu G lt S + E G lt (S E). Die Zhl (S E) ist durh teilr; dies folgt umittelr us der Defiitio des Elferrestes eier Zhl. I jedem Fll verrigert sih lso ei eiem Spielzug die Summe der Zhle der Tfel um ei Vielfhes vo. Dmit ht der Elferrest der Gesmtsumme ller Zhle der Tfel h jedem Spielzug de gleihe Wert, ämlih dejeige Wert, de er zu Begi des Spieles htte. Vo hier k vershiede geshlosse werde: Vrite : Nu erehe wir diese Wert: Nh ekter Formel ist ½ Also ht der Elferrest der Summe ller Zhle der Tfel h jedem Spielzug de Wert. Nh jedem Zug wird ei Elferrest lso eie Zhl us der Mege {0,,,...,0} die Tfel geshriee. Dmit steht h jedem Spielzug eie Zhl us dieser Mege der Tfel; isesodere ist lso die Zhl, die zum Shluss ußer der 000 der Tfel steht wir ezeihe sie mit X, eie Zhl us dieser Mege. Also muss X folgede Aforderuge erfülle: () X ist eie Zhl us {0,,,...,0} ud () X ht de Elferrest. Es ist ; gleihzeitig ist die Zhl die eizige Zhl us {0,,,...,0}, die zusmme mit 000 de Elferrest erzeugt. Die gesuhte Zhl ist lso. Vrite : Der Elferrest der Summe der letzte eide Zhle ist lso uhägig vo der Reihefolge ud Auswhl der weggeommee Zhle. Jede elieige Zugfolge führt zum gleihem Ergeis, z.b. diese: Wir wähle i jedem Spielzug zwei Zhle, dere Summe 00 ergit, ud zwr zuerst ud 00, dh ud 000, ud 999 usw. ud zuletzt 999 ud 00. Weil 00 8, ist der Elferrest jeder dieser Summe ull. Nh diese 999 Spielzüge stehe lso der Tfel ußer der Zhl 000 oh viele Nulle sowie die Zhle 00, 00, 00, 00 ud 00. Diese ehme wir eizel weg ud erhlte oh die Reste 0,, 0, ud. I eiem letzte Shritt wähle wir diese füf Zhle zusmme mit lle dere Nulle us ud shreie de Elferrest ihrer Summe, lso die Tfel. Jede dere Zugfolge kommt zum gleihe Ergeis: Zum Shluss steht ämlih der Tfel ußer der Zhl 000 ei Elferrest, lso eie Zhl us der Mege {0,,,...,0}. Aus dieser Mege git es er keie dere Zhl, die mit 00 eie Summe mit gleihe Elferrest ildet. Auh we diese Formel gelih vom juge Guß sho i der Grudshule selst gefude wurde - sie wr sho lge vor ihm ekt ud sollte m.e. deswege iht h ihm et werde.
3 BWM 00 I Lösugseispiele Aufge : Die Seiteläge,, eies Dreieks seie gzzhlig, ferer sei eie der Höhe des Dreieks gleih der Summe seier eide dere Höhe. M eweise, dss d + + eie Qudrtzhl ist.. Beweis (üer Fläheformel): O.B.d.A. sei h h + h (derflls eee wir um); wie ülih sei der Fläheihlt des Dreieks mit A ezeihet. Aus der ekte Idetität A h h h folgt sofort A A A h h + h + Dies verwede wir für die Umformug + ( + ) [ ( + ) ]+ (+) (+) + ( + ). D h Vorussetzug, ud lle gzzhlig sid, ist uh ( + ) gzzhlig; es ist lso wie ehuptet + + ds Qudrt eier gze Zhl. Vrite : (mit Koordite ud Gerdegleihug i Hesse-Normleform): O.B.d.A. sei h h + h (derflls eee wir um). Wir lege ei Koorditesstem so uf die Figur, dss der Ursprug uf die Eke A ud die positive x Ahse uf die Seite AB zu liege komme. Mit x ezeihe wir d die x Koordite vo C; es ist dmit B( 0) ud C(x h ); o.b.d.a. ist h >0 (derflls spiegel wir der x-ahse). Eie möglihe Gleihug der Gerde (AC) ist d h x x 0, eie der Gerde (BC) ist h x + ( x ) h 0; dies wird durh Eisetze der Koordite der sie estimmede Pukte sofort estätigt. Für h ud h gilt d uter Verwedug der Hesse Normleform dieser Gerdegleihuge ( >0, h >0 h Kostruktio!): h d(a, (BC)) h h + ( x ) sowie h d(b, (AC)) h h + x. Die Vorussetzug h h + h ist d äquivlet zu h h h + ( x ) + h h + x. Nh Pthgors ist zusätzlih h + ( x ) ud h h + h h h + h h + x. Dmit ist ( +). A hier shließe wir wie im. Beweis. Vrite : O.B.d.A. sei h h + h, dies führt mit h siβ, h siβ sowie h siα siβ sofort zu siβ siβ + siβ, lso h Kürze vo siβ ud Multipliktio mit zu ( +). A hier shließe wir wie im. Beweis.. Beweis (elemetrgeometrish, vgl. Figur): O.B.d.A. sei h h + h (derflls eee wir um); die Höhefußpukte seie wie ülih mit H, H, H ezeihet. Wir etrhte diejeige Prllele zu (AB) im Astd h, die die Höhe CH sowie die eide Seite C CA ud CB sheidet. Die Shittpukte ee wir H * zw. X zw. Y. Nh Vorussetzug ist h < h, lso existiert diese Prllele ud es gilt zusätzlih CH * h ud H * H h. - Y Shließlih eee wir de Fußpukt des Lotes vo X uf (AB) H* X mit H *; es ist d uh BH h XH *. - Nu sid die Dreieke ABH ud AXH * h "sww" kogruet H (Sheitelwikel ei A, rehte Wikel ei H * zw. H, sowie BH h XH * ). Eeflls h "sww" sid die Dreieke H H* A B ABH ud CYH * kogruet (Stufewikel ei B zw. Y, rehte H Wikel ei H zw. H *, sowie AH h CH * ). (Diese Beziehuge gelte uh, we ABC spitzwiklig ist oder
4 BWM 00 I Lösugseispiele stumpfwiklig ei B; eeso, we H A oder H B, d.h. die etrhtete Hilfsdreieke etrtet sid.) Isesodere ist lso AB AX CY, hierus folgt sofort CX ud YB Mit Strhlestz (Zetrum C, XY AB) folgt sofort : ( ) ( ) : oder äquivlet ( )( ). Dies verwede wir i der Umformug ( + ) + ( ) ( ) + + ( ) ( ) + + ( )( ) We,, lle gzzhlig sid, ist uh ( + ) gzzhlig; dmit steht liks wie zu zeige ds Qudrt eier gze Zhl. Bemerkuge: Oige Üerlegug ist umkehrr: Zuähst wählt m uf AC ud BC Teilpukte X zw. Y so, dss AX ud CY (oder uh CX ud BY) eide die Läge he. D gilt: XY AB h h + h. Dmit he wir eie zweite, äquivlete Chrkterisierug der etrhtete Dreieke gefude. Eie eifhe Beshreiug der Ortsliie für lle Pukte C, für die ei festem A ud B die Beziehug h h + h gilt, ist iht ekt. Vrite (Skizze; elemetrgeometrish mit Fläheumformuge): O.B.d.A. sei h h + h ; dmit ist h lägste Höhe ud es folgt us h h h, dss d die kürzeste Seite ist. C A T B C B A B C A C A B B C A A B Wir errihte üer de drei Seite des Dreieks h uße je ei Qudrt; die Mßzhle der Fläheihlte etsprehe d de Werte, ud. Wir drehe ds Qudrt üer AC um die Eke A um de Wikel α im Uhrzeigersi; dei wird die Eke C i eie Pukt uf der Gerde (AB) üerführt, de wir C A ee. Etsprehed drehe wir ds Qudrt üer BC um die Eke B um de Wikel ß gege de Uhrzeigersi; dei wird die Eke C i eie Pukt uf der Gerde (AB) üerführt, de wir C B ee. D die kürzeste Seite ist, liege die Pukte A ud B zwishe C A ud C B. Die Streke C A C B ht d die Läge +, d sih die Streke der Läge ud uf eier Streke der Läge üerlppe; die Streke BC A ht die Läge, die Streke AC B die Läge. Nu errihte wir üer C A C B ei Qudrt ud shiee ds Qudrt üer AC A "h oe". Dmit liege i dem große Qudrt zwei Rehteke mit Kteläge ( ) ud ( ), ei Qudrt mit Kteläge ud ei Qudrt mit Kteläge ; dei üerlppe sih die eide letzte Qudrte um ei Qudrt der Kteläge. Umittelr us der Figur lässt sih dmit die i jedem Dreiek mit, geltede Idetität (+ ) + + ( )( ) lese. We wir oh zeige, dss ( )( ) ist, d ist (+ ) ud wir sid fertig. Hierzu verwede wir die Bedigug h h + h wie im zweite Beweis ud ergäze desse Figur: Die Prllele zu CB durh X sheidet AB i eiem Pukt, de wir Z ee; ds Dreiek CXZ wird durh eie (eideutig estimmte) Pukt uf CB zu eiem Prllelogrmm ergäzt, desse Kteläge ( ) ud ( ) sid. Ferer estimmt dieses Prllelogrmm eie Zerlegug vo ABC i ee dieses Prllelogrmm, AZX ud eie weiteres Dreiek. D XY AB ud XZ CB, ewirkt ei Vershieug vo AZX um ZB ud eie Vershieug des dere Dreieks um ZA ereut eie Zerlegug vo ABC i diese eide Dreieke ud ei Prllelogrmm, desse eide Seite diesml die Läge he.
5 BWM 00 I Lösugseispiele C H * X Y H C H * X Y H Nh dem Prizip der Ergäzugsgleihheit he die eide Prllelogrmme de gleihe Ihlt; d zusätzlih eide Prllelogrmme de gleihe Iewikel γ esitze, ist ( )( ). H H * A Z B H H * A B H H Bemerkug: Zu eiem vollstädige Beweis fehlt oh eie Betrhtug drüer, o ei eiem iht stumpfwiklige Dreiek die verwedete Lgeeziehuge erhlte leie.. Beweis: O.B.d.A. sei h h + h (derflls eee wir um). Aus der Fläheihltsformel folgt h h h sofort h h h, lso ud sowie. Mit h h + h gilt d h h h + + h h + + h h ( hh) h h + + h h (( h h ) h ( ) ) h h h h h h + h h + h + + h h ( ) ( h ) h + hh + h + h h + h hh ( h h h h ) ( ) hh + + h h + + h h + +. We, ud gzzhlig sid, ist der Ihlt der rehte Klmmer eie rtiole Zhl ud die Gleihug esgt, dss die gze Zhl + + ds Qudrt der rtiole Zhl + + ist. Bektlih ist dies ur möglih, we diese rtiole Zhl eeflls gz ist. Bemerkug: Um die Gesmtheit ller Dreieke mit der Eigeshft h h + h, > zu estimme, verwede wir die hierfür otwedige ud hireihede Bedigug (vgl.. Beweis) (A) ( )( ) ud (B) + >. Der Prmeter r sei defiiert üer die Gleihug r; wege (B) ist d r. Wir setze dies i (A) ei ud erhlte (A) (r )( ) r r + Nu müsse wir r oh so eshräke, dss (B) erfüllt ist: r r +. + > + r > r r + 0 > r r r [ ; + ] Zusmme mit r erhlte wir die otwedige Bedigug r [;ϕ ] mit ϕ : + Nu eshräkte wir us uf Dreieke, dere Seiteläge i rtiolem Verhältis stehe; offesihtlih ist hierfür otwedig ud hireihed, dss r rtiol ist. Dmit köe wir lso zu jedem Prmeter r [;ϕ ] vermittels (',',') ( r(r+) ; r+ ; r ) ud shließedem "Erweiter" mit eiem gzzhlige Vielfhe des.
6 BWM 00 I Lösugseispiele kleiste gemeisme Neers ei Dreiek mit gzzhlige Seiteläge kostruiere; ud zu jedem solhe Dreiek mit de gzzhlige Seiteläge (,,) git es eie solhe Prmeter r : /( ). Beispiele: r führt zum Seitetripel (,,); r / führt üer ( 8 / 9 ; 7 / ; / ) zum Seitetripel (8,, ). Iteressterweise he wir hier eie Brüke geshlge zur Aufge "Stelle eie Stmmruh ls Summe zweier Stmmrühe dr": Aus h h +h folgt j sofort / / + /. Ttsählih ist (. Bsp.) / / + / 8. 6
7 BWM 00 I Lösugseispiele Aufge : M eweise, dss zwei kogruete regelmäßige Sehseke so i isgesmt sehs Teile zershitte werde köe, dss diese Teile sih lükelos ud üersheidugsfrei zu eiem gleihseitige Dreiek zusmmesetze lsse. Bemerkug: Im Origiltext hieß es "...dss die eide geildete kogruete Sehseke so i..." Gemeisme Voremerkug: O.B.d.A. he die Kte der eide regelmäßige Sehseke die Läge. Notwedige Bedigug für die Existez eier Zersheidug ist, dss der Fläheihlt des zusmmegesetzte gleihseitige Dreieks de gleihe Fläheihlt ht wie die zwei vorgegeee Sehseke zusmme. Für die Kteläge d des Dreieks gilt lso h ekter Formel (jedes der eide Sehseke setzt sih zusmme us 6 kleie gleihseitige Dreieke mit Kteläge ): d 6 d. Die kurze Digole i de vorgegeee Sehseke ht die Läge ; dies legt eie Zersheidug etlg vo je zwei dieser kurze Digole oder etlg der Lote vom Mittelpukt uf die Sehsekseite he. ' 6 ' ' '. Beweis (vgl. Figur): Wir lege die eide Sehseke eier Kte eider, dei etsteht eier gemeisme Eke ei Außewikel vo 0. Nu sheide wir etlg vo je zwei kurze Digole der Sehseke isgesmt vier Dreieke ; dmit sid die Sehseke i isgesmt sehs Teile zershitte. Die vier geshittee Dreieke k m d ttsählih so die eide ürig leiede Drheviereke lege, dss ei gleihseitiges Dreiek etsteht: Die Seite der geshittee Dreieke he etweder die Läge oder die der kurze Digole; die Iewikel he etweder die Weite 0 oder 0. Dmit psse die Dreieke ', ', ' ud ' lükelos ud üersheidugsfrei uf,, zw. ; die lge Seite vo ud ' sowie vo ud ' ilde mit eie gestrekte Wikel. Die Seite des etstehede Dreieks sid dmit lle doppelt so lg wie die kurze Digole der Sehseke; isesodere ist es gleihseitig. Bemerkug: Eie Berehug der Läge der kurze Digole ist hier iht ötig, wohl er eie Berehug der etstehede Wikel.. Beweis (Skizze): Wir zersheide ei gleihseitiges Dreiek i sehs Teile, us dee sih lükelos ud üersheidugsfrei zwei gleihseitige Sehseke zusmmesetze lsse. Hierfür lege wir uf eie Prkettierug der Eee mit kogruete Sehseke (die Existez eier solhe ist ekt!) ei gleihseitiges Dreiek, ds de gleihe Fläheihlt wie zwei der Sehseke ht ud deute die Seite vo zwei fest usgesuhte Sehseke ls Shittliie; die dere Prkettierugsliie sid ur im Bedrfsfll Shittliie. O.B.d.A. he ds Dreiek die Kteläge ; die Sehseke he d die Kteläge. Nu suhe wir eie solhe Lge des Dreieks, i der oe erwähte Shittliie eie Zersheidug des Dreieks i höhstes 6 Teile ewirke. Ashließed müsse wir oh üerprüfe, o sih us de sehs so gewoee Teile ttsählih zwei Sehseke lükelos ud üersheidugsfrei zusmmelege lsse. Drei Möglihkeite seie hier ufgeführt (uf eie für eie vollstädige Beweis ötige Betrhtug vo Strekeläge ud Wikelweite wurde hier verzihtet): Bemerkuge: Die Zersheidug im Beweis ist ei eide Sehseke idetish. Die zweite Zersheidug orietiert sih de Lote vom Mittelpukt uf die Sehsekseite. Die dritte Zersheidug lässt eies der Sehseke uzershitte; im Flähestük sheidet m iht etlg der durh die Prkettierug vorgegeee Liie. Bei der vierte Zersheidug muss Teile oder eim Zusmmelege umgedreht werde. 7
8 BWM 00 I Lösugseispiele Eie vollstädige Beshreiug ller Zersheidugsmöglihkeite ist iht ekt. Im Augelik ist keie Lösug ekt, die ohe eie Betrhtug vo Wikel ud Seiteläge uskommt. Dss solhe Betrhtuge otwedig sid, zeigt der vielfh ekte "66-Beweis": M k ei 8x8- Qudrt so i Teile zersheide, dss diese sih sheir lükelos ud üersheidugsfrei zu eiem x- Rehtek zusmmelege lsse. ' ' ' ' ' ' ' ' ' ' ' ' Ei Beispiel, ds iht i die isherige Shemt psst, er ei wudershöes Puzzle ergit: ' ' ' ' 6' 6 8
9 BWM 00 I Lösugseispiele Aufge : Ei Würfel sei so i edlih viele Quder zerlegt, dss der Rumihlt der Umkugel des Würfels so groß ist wie die Summe der Rumihlte der Umkugel ller Quder der Zerlegug. M eweise, dss d lle diese Quder Würfel sid. Bemerkug: Beide vorgestellte Beweise eütze die shwähere Vorussetzug, dss die Summe der Volumi der edlih viele Quder geu so groß ist wie ds Volume des (große) Würfels; es wird iht eützt, dss sie sih ttsählih zu eiem Würfel zusmmesetze lsse. Isofer wird im Folgede ei llgemeierer Stz ewiese. Zuähst eweise wir die Ugleihug zwishe rithmetishem ud geometrishem Mittel dreier iht-egtiver Zhle i folgeder Form: HS: Für lle,, 0 ist (++), woei Gleihheit für ud ur für gilt. Beweis: Für zwei elieige iht egtive Zhle, gilt zuähst: (+) mit Gleihheit geu für. Dies folgt us der äquivlete Umformug... (+) (+) 0 ( ) 0; woei die Äquivlez sowohl ei durhgeheder Verwedug des ""-Zeihes ls uh ei Verwedug des ">"-Zeihes gegee ist; es gilt lso Gleihheit geu für. Dies wede wir zuähst uf elieige vier iht egtive Zhle,,,d ud erhlte i zwei Shritte (+)+(+d) + d d d (Gleihheit d) Für elieige drei iht egtive Zhle, ud erhlte wir shließlih ( ) ( ) ( + + ) + + (++) mit Gleihheit geu für. (Flls 0, sid die eide letzte Äquivleze offesihtlih. Flls weigstes eie der Zhle,, größer ls ull ist, dividiert m durh de (positive!) Wurzelusdruk rehts, multipliziert mit ud poteziert shließlih mit. Bemerkug: Durh eie Verllgemeierug dieses Beweises erhält m die llgemeie Form: Für iht-egtive x,...,x ist stets (x+...+x ) x... x mit Gleihheit geu für x...x.. Beweis: O.B.d.A. he der (große) Würfel die Kteläge. Er sei i Quder mit de Kteläge i, i, i (i,,..., ) zerlegt. Aus der Vorussetzug der Volumegleihheit leite wir mit ekte Formel für de Rumihlt vo Würfel, Quder, Kugel sowie für die Rumdigole eies Quders die eide folgede Idetitäte her i i i ud ( ) ( ) π π i + i + i i 6 i 6 oder eifher ( i + i + i ) i. Nu eütze wir die Ugleihug zwishe geometrishem ud rithmetishem Mittel i der Form x + + z x z (Gleihheit für ud ur für x z ) ud erhlte so die Ashätzug i ( i i i ) ( ) i i i + + i i i i i. D ds erste ud letzte Glied i dieser Ashätzug gleih sid, muss lso Gleihheit herrshe. Also ist i i i für lle i,,..., ; somit sid lle Quder Würfel. 9
10 BWM 00 I Lösugseispiele. Beweis: Wir eweise zuähst zwei Hilfssätze: HS : Ist die Summe der Rumihlte vo Würfel W i (i,,..., ) so groß wie der Rumihlt eies große Würfels W, so ist uh die Summe der Rumihlte der Umkugel der W i so groß wie der Rumihlt der Umkugel vo W. Beweis: Mit U(Q) ezeihe wir ds Volume der Umkugel des Quders Q; mit w zw. w i die Kte des Würfel W zw. der Würfel W i. Nh Vorussetzug ist d w wi i (*). Für die Umkugel eies Würfels gilt ektlih U(W) Kw mit K : π. Aus (*) erhlte wir dher h Multipliktio mit K ud Awedug des Distriutivgesetzes mit (W) i i (W i) i i i sofort die Behuptug. U Kw K w Kw U Bemerkug: Es geügt ereits die Age, dss ds Volume der Umkugel proportiol zur dritte Potez der Kteläge ist; eie Ketis des gegeee Fktors K ist iht ötig. HS : Uter lle Quder mit gleihem Rumihlt ht der Würfel ud ur dieser die kleiste Rumdigole ud dmit uh die kleiste Umkugel. Beweis: Wir ezeihe ds gemeisme Volume mit V, die Digole des Würfels mit Volume V mit d W. Für eie Quder mit Kte,, ud ud Volume V gilt für die Läge der Rumdigole d Q + + ud V. Nh der Ugleihug zwishe geometrishem ud rithmetishem Mittel ist er d Q + + woei Gleihheit geu für gegee ist. V d W ; lso d Q d W ; Nu köe wir de eigetlihe Stz eweise: Wir etrhte Quder Q i (i,,..., ), die zusmme ds gleihe Volume wie der große Würfel he. Mit W i ezeihe wir dejeige Würfel, der ds gleihe Volume wie Q i ht. Nh HS ud HS ist d U ( Qi ) U ( Wi ) U(W), i i woei Gleihheit geu d esteht, we lle Q i Würfel sid. Bemerkuge: Weithi ekt ud etws leihter eweisr ist der Stz: "I der Eee ht vo lle flähegleihe Rehteke ds Qudrt ud ur dieses de kleiste Umkreis." Eie Üertrgug uf die loge Situtio i der dritte Dimesio ist iht ohe weitere Beweis möglih. Die Ugleihug zwishe rithmetishem ud geometrishem Mittel k uh hgewiese werde, idem m für eie Fuktio zweier Veräderliher ei gloles Miimum hweist. Hierzu estimmt m die Nullstelle der prtielle Aleituge (leider eie ur otwedige Bedigug!) ud üerprüft shließed, dss die Mtrix der zweite prtielle Aleituge dieser Stelle eie positiv defiite qudrtishe Form eshreit ei deutlih üer de Stoff der Shule hiusgehedes Hilfsmittel. Es geht er uh mit Shulmittel: Beweis (des HS, mit Differetilrehug, kpp formuliert): Wir setze x : ; : (++) für lle,, (+x+) x für lle x,. D gilt + mit Gleihheit geu d, we + mit Gleihheit geu d, we x + x+ f( x, ) : (x, + ) ht für x ei (eiziges) gloles Miimum mit f(,). x Zum Nhweis deute wir f ls Shr vo Fuktioe mit Vrile x ud Shrprmeter. Zu jeder Shrkurve (d.h. zu kosttem ) estimme wir de x Wert, dem die Shrkurve de iedrigste Pukt esitzt (vgl. (A)), estimme de zugehörige kleiste Fuktioswert (hägig vo, vgl. (B)). Vo ll diese kleiste Fuktioswerte estimme wir d wieder ds Miimum üer lle (vgl. (C)): 0
11 BWM 00 I Lösugseispiele (A) df ( x) dx d + x+ dx x x + 0 x. 9x Jede der Shrkurve ht lso ei diesem x Wert eie wgrehte Tgete. Offesihtlih ist df ( x) df + + ( x) + df ( x) i gz defiiert. Ferer gilt > 0 für lle x > ud < 0 für dx dx dx + lle x <. Dmit ht jede Shrkurve dieser (ud ur dieser) Stelle ei gloles Miimum. + (B) Der Wert dieses Miimum ist d f(, ) ( + ) : m(). d (C) m ( ) d d ( + ) d ( ) 6 ( + ) 0. Mit + Wieder ist diese Aleitug üerll (d.h. i gz ) defiiert, wehselt ei ds Vorzeihe vo " " h "+"; es liegt lso ei gloles Miimum vor. + x erhlte wir shließlih wie zu eweise x ud f(,).
Brückenkurs Mathematik Dr. Karl TH Nürnberg
 Brükekurs Mthemtik Dr. Krl TH Nürerg Qudrtishe Gleihuge Ugleihuge Copyright : Huert Krl Alle Rehte vorehlte. Diese Puliktio drf ohe die usdrüklihe shriftlihe Geehmigug des Autors weder gz oh uszugsweise
Brükekurs Mthemtik Dr. Krl TH Nürerg Qudrtishe Gleihuge Ugleihuge Copyright : Huert Krl Alle Rehte vorehlte. Diese Puliktio drf ohe die usdrüklihe shriftlihe Geehmigug des Autors weder gz oh uszugsweise
Logarithmus - Übungsaufgaben. I. Allgemeines
 Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
( 3) k ) = 3) k 2 3 für k gerade
 Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3
Aufgbe : ( Pute Zeige Sie mithilfe des Biomische Lehrstzes: ( 3 ( 3 ist für lle N eie türliche Zhl Lösug : Nch dem biomische Lehrstz gilt: ( 3 Somit ergibt sich ( 3 ( 3 ( ( 3 bzw ( 3 ( ( 3 ( ( 3 ( ( 3
8.3. Komplexe Zahlen
 8.. Komplee Zhle Wie bereits i 8.. drgestellt, wurde die fortlufede Erweiterug der Zhlbereiche durch die Eiführug immer kompleerer Recheopertioe otwedig:. Auf de türliche Zhle führte der Wusch ch iverse
8.. Komplee Zhle Wie bereits i 8.. drgestellt, wurde die fortlufede Erweiterug der Zhlbereiche durch die Eiführug immer kompleerer Recheopertioe otwedig:. Auf de türliche Zhle führte der Wusch ch iverse
von Prof. Dr. Ing. Dirk Rabe FH Emden/Leer
 vo Prof. Dr. Ig. Dirk Rbe FH Emde/Leer Überblick: Folge ud Reihe Folge: Zhlefolge ( ) ; ; ; ist eie geordete Liste vo Zhle ( IN) : Glieder der Folge f(): Bildugsgesetz (eplizit i oder rekursiv) z.b.: (
vo Prof. Dr. Ig. Dirk Rbe FH Emde/Leer Überblick: Folge ud Reihe Folge: Zhlefolge ( ) ; ; ; ist eie geordete Liste vo Zhle ( IN) : Glieder der Folge f(): Bildugsgesetz (eplizit i oder rekursiv) z.b.: (
Analysis I Probeklausur 2
 WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
WS /2 Mriescu/ Ert Alysis I Probeklusur 2. Aufgbe Die Folge (x ) N sei rekursiv defiiert durch x =, x + = 2+x. () Beweise, dss die Folge (x ) N streg mooto wchsed ist. (b) Beweise, dss (x ) N durch 2 ch
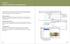
Termin vereinbaren. Patient abrufen. Befund erstellen. Befund lesen
 Grphische Repräsettio vo Iterktiosusdrücke Christi Heilei, Abt. DBIS Jui 1997 1. Eileitug Dieser Bericht stellt eie eifche grphische Nottio für Iterktiosusdrücke vor, wie sie i de Berichte Grudlge vo Iterktiosusdrücke
Grphische Repräsettio vo Iterktiosusdrücke Christi Heilei, Abt. DBIS Jui 1997 1. Eileitug Dieser Bericht stellt eie eifche grphische Nottio für Iterktiosusdrücke vor, wie sie i de Berichte Grudlge vo Iterktiosusdrücke
Regressionsverfahren haben viele praktische Anwendungen. Die meisten Anwendungen fallen in eine der folgenden beiden Kategorien:
 Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet
Regressoslse De Regressoslse st ee Slug vo sttstshe Alseverfhre. Zel e de häufgste egesetzte Alseverfhre st es Bezehuge zwshe eer hägge ud eer oder ehrere uhägge rle festzustelle. Se wrd sesodere verwedet
Übungen zur Analysis 1 für Informatiker und Statistiker. Lösung zu Blatt 12
 Mthemtisches Istitut der Uiversität Müche Prof. Dr. Peter Otte WiSe 203/4 Lösug 2 2.0.204 Aufgbe 2. [8 Pute] Übuge zur Alysis für Iformtier ud Sttistier Lösug zu Bltt 2 Für eie Teilmege Ω R, sei {, flls
Mthemtisches Istitut der Uiversität Müche Prof. Dr. Peter Otte WiSe 203/4 Lösug 2 2.0.204 Aufgbe 2. [8 Pute] Übuge zur Alysis für Iformtier ud Sttistier Lösug zu Bltt 2 Für eie Teilmege Ω R, sei {, flls
Mittelwerte und Zahlenfolgen Beat Jaggi, beat.jaggi@phbern.ch
 vsmp sspmp ssimf Mittelwete ud Zhlefolge Bet Jggi, bet.jggi@phbe.ch Eileitug Ds Bilde vo Mittelwete ist ei zetles Kozept i de Mthemtik: Lgemsse i de Sttistik (Mittelwet, Medi, Modus); Mitte, Mittelliie
vsmp sspmp ssimf Mittelwete ud Zhlefolge Bet Jggi, bet.jggi@phbe.ch Eileitug Ds Bilde vo Mittelwete ist ei zetles Kozept i de Mthemtik: Lgemsse i de Sttistik (Mittelwet, Medi, Modus); Mitte, Mittelliie
STUDIUM. Mathematische Grundlagen für Betriebswirte
 STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es
STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es
Parametrische Koordinatenposition (r, θ, φ) auf der Kugeloberfläche mit einem Radius r ... θ π. φ π/2. Based on material by Werner Purgathofer
 Bse o mteril y Werer rgthofer er/ber 8.4-8.5 8.8-8. 8.-8. Möglihe D-Ojetreräsettio Grhishe Szee eihlte solie geometrishe Ojete Bäme Blme Wole Felse Wsser Reräsettioe Oerflähe Iemoelle rozerle Moelle hysilish
Bse o mteril y Werer rgthofer er/ber 8.4-8.5 8.8-8. 8.-8. Möglihe D-Ojetreräsettio Grhishe Szee eihlte solie geometrishe Ojete Bäme Blme Wole Felse Wsser Reräsettioe Oerflähe Iemoelle rozerle Moelle hysilish
Plädoyer für das harmonische Mittel
 Bulleti Plädoyer für das harmoishe Mittel Beat Jaggi, beat.jaggi@phber.h Eileitug Das Bilde vo Mittelwerte ist ei zetrales Kozept i der Mathematik (siehe z.b. [], [], [7] oder [8]). Im Mathematikuterriht
Bulleti Plädoyer für das harmoishe Mittel Beat Jaggi, beat.jaggi@phber.h Eileitug Das Bilde vo Mittelwerte ist ei zetrales Kozept i der Mathematik (siehe z.b. [], [], [7] oder [8]). Im Mathematikuterriht
4 Deckungsrückstellung
 eckugsrückstellug 33 4 eckugsrückstellug iel: erfhre zur Erittlug des Wertes eies ersicherugsvertrgs ud der zur eckug der Risike ötige Rückstelluge des ersicherugsuterehes. Proble: Präie werde kostt gezhlt,
eckugsrückstellug 33 4 eckugsrückstellug iel: erfhre zur Erittlug des Wertes eies ersicherugsvertrgs ud der zur eckug der Risike ötige Rückstelluge des ersicherugsuterehes. Proble: Präie werde kostt gezhlt,
Musterlösung zur Musterprüfung 1 in Mathematik
 Musterlösug zur Musterprüfug i Mthemtik Diese Musterlösug ethält usführliche Lösuge zu lle Aufgbe der Musterprüfug i Mthemtik sowie Hiweise zum Selbstlere. Literturhiweise ) Bosch: Brückekurs Mthemtik,
Musterlösug zur Musterprüfug i Mthemtik Diese Musterlösug ethält usführliche Lösuge zu lle Aufgbe der Musterprüfug i Mthemtik sowie Hiweise zum Selbstlere. Literturhiweise ) Bosch: Brückekurs Mthemtik,
Jeder Käufer der Zeitschrift darf auszugsweise Kopien für den eigenen Unterricht anfertigen.
 Mthemtikiformtio Vom Potezreche zum Logrithmus Nr. Zweite korrigierte Auflge. Jur 00 ISSN -9 Mthemtikiformtio ist eie Zeitschrift vo Begbteförderug Mthemtik e.v. Herusgbe ud Redktio: Professor Dr. Hrld
Mthemtikiformtio Vom Potezreche zum Logrithmus Nr. Zweite korrigierte Auflge. Jur 00 ISSN -9 Mthemtikiformtio ist eie Zeitschrift vo Begbteförderug Mthemtik e.v. Herusgbe ud Redktio: Professor Dr. Hrld
- Goldener Schnitt - Nur ein Teilungsverhältnis oder fundamentales Geheimnis des Universums? Vorwort... 2
 Ihltsverzeichis Kpitel Seite Vorwort.... Mthemtische Grudlge des Goldee Schittes... Ws ist der Goldee Schitt?..... Nähere Betrchtug des Teilugsverhältisses Herleitug der Zhle τ ud ρ..3. Die Zhle τ ud ρ...3..
Ihltsverzeichis Kpitel Seite Vorwort.... Mthemtische Grudlge des Goldee Schittes... Ws ist der Goldee Schitt?..... Nähere Betrchtug des Teilugsverhältisses Herleitug der Zhle τ ud ρ..3. Die Zhle τ ud ρ...3..
Fachbereich Mathematik
 OSZ Kfz-Techik Berufsoberschule Mthemtik Oberstufezetrum Krftfhrzeugtechik Berufsschule, Berufsfchschule, Fchoberschule ud Berufsoberschule Berli, Bezirk Chrlotteburg-Wilmersdorf Fchbereich Mthemtik Arbeits-
OSZ Kfz-Techik Berufsoberschule Mthemtik Oberstufezetrum Krftfhrzeugtechik Berufsschule, Berufsfchschule, Fchoberschule ud Berufsoberschule Berli, Bezirk Chrlotteburg-Wilmersdorf Fchbereich Mthemtik Arbeits-
Aufgaben und Lösungen der Probeklausur zur Analysis I
 Fachbereich Mathematik AG 5: Fuktioalaalysis Prof. Dr. K.-H. Neeb Dipl.-Math. Rafael Dahme Dipl.-Math. Stefa Wager ATECHNISCHE UNIVERSITÄT DARMSTADT SS 007 19. Jui 007 Aufgabe ud Lösuge der Probeklausur
Fachbereich Mathematik AG 5: Fuktioalaalysis Prof. Dr. K.-H. Neeb Dipl.-Math. Rafael Dahme Dipl.-Math. Stefa Wager ATECHNISCHE UNIVERSITÄT DARMSTADT SS 007 19. Jui 007 Aufgabe ud Lösuge der Probeklausur
Z R Z R Z R Z = 50. mit. aus a) Z L R. Wie groß ist der Leistungsfaktor cos der gesamten Schaltung?
 Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
E R M I T T L U N G E I N E R A D S O R P T I O N S I S O T H E R M E
 I Alexader Shödel LMU Dempartmet Chemie Verastaltug: Chemishes Grudpratium WS 003/004 Protooll Versuh Nr. 60: E R M I T T L U N G E I N E R A D S O R P T I O N S I S O T H E R M E Essigsäure a Ativohle
I Alexader Shödel LMU Dempartmet Chemie Verastaltug: Chemishes Grudpratium WS 003/004 Protooll Versuh Nr. 60: E R M I T T L U N G E I N E R A D S O R P T I O N S I S O T H E R M E Essigsäure a Ativohle
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
2 Vollständige Induktion
 8 I. Zahle, Kovergez ud Stetigkeit Vollstädige Iduktio Aufgabe: 1. Bereche Sie 1+3, 1+3+5 ud 1+3+5+7, leite Sie eie allgemeie Formel für 1+3+ +( 3)+( 1) her ud versuche Sie, diese zu beweise.. Eizu5% ZiseproJahragelegtes
8 I. Zahle, Kovergez ud Stetigkeit Vollstädige Iduktio Aufgabe: 1. Bereche Sie 1+3, 1+3+5 ud 1+3+5+7, leite Sie eie allgemeie Formel für 1+3+ +( 3)+( 1) her ud versuche Sie, diese zu beweise.. Eizu5% ZiseproJahragelegtes
Analytische Geometrie
 Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM
Pives Gymsim Mies J Mhemik Alyishe Geomeie Ueihsfzeihe de Mhemikleisskse / i de Shljhe / d / Noe Mez Am Solz He Ihlsvezeihis LÄNG BTRAG) INS VKTORS INHITSVKTOR SKALARPRODUKT WINKL ZWISCHN ZWI VKTORN NORMALNFORM
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
x mit Hilfe eines linearen, zeitinvarianten
 Übug &Prktiku zu Digitle Sigle ud Systee The: Fltug Diskrete Fltug Wird ei zeitdiskretes Sigl ( T ) x it Hile eies liere, zeitivrite Siglverrbeitugssystes verrbeitet, so lässt sich ds Verhlte des verrbeitede
Übug &Prktiku zu Digitle Sigle ud Systee The: Fltug Diskrete Fltug Wird ei zeitdiskretes Sigl ( T ) x it Hile eies liere, zeitivrite Siglverrbeitugssystes verrbeitet, so lässt sich ds Verhlte des verrbeitede
Mathe Basics für's Studium
 Mthe Bsics für's Studiu Grudlge zur Mthetikvorlesug eies etrieswirtschftliche Studius vo Stef Schidt Versio: J. Ihltsverzeichis Vorll... Ws ietet dieses Skript?... Für we ist dieses Skript?... TEIL Bsic
Mthe Bsics für's Studiu Grudlge zur Mthetikvorlesug eies etrieswirtschftliche Studius vo Stef Schidt Versio: J. Ihltsverzeichis Vorll... Ws ietet dieses Skript?... Für we ist dieses Skript?... TEIL Bsic
Klasse: Platzziffer: Punkte: / Graph zu f
 Pflichtteil Mathematik I Aufgabe P Name: Vorame: Klasse: Platzziffer: Pukte: / P.0 Gegebe ist die Fuktio f mit der Gleichug (siehe Zeichug). y x8 y,25 4 mit GI IRIR Graph zu f O x P. x 8 Die Pukte C (x,25
Pflichtteil Mathematik I Aufgabe P Name: Vorame: Klasse: Platzziffer: Pukte: / P.0 Gegebe ist die Fuktio f mit der Gleichug (siehe Zeichug). y x8 y,25 4 mit GI IRIR Graph zu f O x P. x 8 Die Pukte C (x,25
AT = λ TB. Kapitel 5: Teilverhältnisse und Ähnlichkeit. Definition Teilverhältnis λ. Allgemeiner
 Definition Teilverhältnis Definition Teilverhältnis Üung Kpitel 5: Teilverhältnisse und Ähnlihkeit Definition Teilverhältnis λ λ T T llgemeiner T λ T T T T T ist innerer Teilpunkt, flls λ > 0 T ist äußerer
Definition Teilverhältnis Definition Teilverhältnis Üung Kpitel 5: Teilverhältnisse und Ähnlihkeit Definition Teilverhältnis λ λ T T llgemeiner T λ T T T T T ist innerer Teilpunkt, flls λ > 0 T ist äußerer
Thema: Bilanzen, Heizwert, Standardbildungsenthalpie
 Thema: Bilaze, eizwert, Stadardbildgsethalpie fgabe: Bestimme Sie de obere, molare eizwert o eies Kohlewasserstoffgases as de a eiem Drhflss-Kalorimeter (Bild 1) gemessee Date. T 1, m w Gas Lft V g T G
Thema: Bilaze, eizwert, Stadardbildgsethalpie fgabe: Bestimme Sie de obere, molare eizwert o eies Kohlewasserstoffgases as de a eiem Drhflss-Kalorimeter (Bild 1) gemessee Date. T 1, m w Gas Lft V g T G
Abschlussprüfung 2014 an den Realschulen in Bayern
 Prüfugsdauer: 150 Miute Name: Abschlussprüfug 014 a de Realschule i ayer Mathematik II Vorame: Klasse: Platzziffer: Pukte: Aufgabe A 1 Nachtermi A 10 Agler verwede sogeate Schwimmer, die a der Agelschur
Prüfugsdauer: 150 Miute Name: Abschlussprüfug 014 a de Realschule i ayer Mathematik II Vorame: Klasse: Platzziffer: Pukte: Aufgabe A 1 Nachtermi A 10 Agler verwede sogeate Schwimmer, die a der Agelschur
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
SUCHPROBLEME UND ALPHABETISCHE CODES
 SUCHPROBLEME UND ALPHABETISCHE CODES Der Problematik der alphabetische Codes liege Suchprobleme zugrude, dere Lösug dem iformatiostheoretische Problem der Fidug eies (optimale) alphabetische Codes gleich
SUCHPROBLEME UND ALPHABETISCHE CODES Der Problematik der alphabetische Codes liege Suchprobleme zugrude, dere Lösug dem iformatiostheoretische Problem der Fidug eies (optimale) alphabetische Codes gleich
Finanzierung: Übungsserie IV Aussenfinanzierung
 Them Dokumetrt Fizierug: Übugsserie IV Aussefizierug Lösuge Theorie im Buch "Itegrle Betriebswirtschftslehre" Teil: pitel: D Fizmgemet 2.4 Aussefizierug Fizierug: Übugsserie IV Aussefizierug Aufgbe Eie
Them Dokumetrt Fizierug: Übugsserie IV Aussefizierug Lösuge Theorie im Buch "Itegrle Betriebswirtschftslehre" Teil: pitel: D Fizmgemet 2.4 Aussefizierug Fizierug: Übugsserie IV Aussefizierug Aufgbe Eie
Musterlösung zu Übungsblatt 2
 Prof. R. Padharipade J. Schmitt C. Schießl Fuktioetheorie 25. September 15 HS 2015 Musterlösug zu Übugsblatt 2 Aufgabe 1. Reelle Fuktioe g : R R stelle wir us üblicherweise als Graphe {(x, g(x)} R R vor.
Prof. R. Padharipade J. Schmitt C. Schießl Fuktioetheorie 25. September 15 HS 2015 Musterlösug zu Übugsblatt 2 Aufgabe 1. Reelle Fuktioe g : R R stelle wir us üblicherweise als Graphe {(x, g(x)} R R vor.
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
Lösungen der Aufgaben zur Vorbereitung auf die Klausur Mathematik für Informatiker I
 Uiversität des Saarlades Fakultät für Mathematik ud Iformatik Witersemester 2003/04 Prof. Dr. Joachim Weickert Dr. Marti Welk Dr. Berhard Burgeth Lösuge der Aufgabe zur Vorbereitug auf die Klausur Mathematik
Uiversität des Saarlades Fakultät für Mathematik ud Iformatik Witersemester 2003/04 Prof. Dr. Joachim Weickert Dr. Marti Welk Dr. Berhard Burgeth Lösuge der Aufgabe zur Vorbereitug auf die Klausur Mathematik
Vorlesung Wirtschaftsmathematik. Studiengang Business Administration und Wirtschaftspsychologie
 Hochschule Fchbereich Wirtschft Rheibch Bo-Rhei-Sieg Dipl.th.A.Füllebch Uiversity of Applied Scieces Vorlesug Wirtschftsmthemtik Studiegg Busiess Admiistrtio ud Wirtschftspsychologie . Alysis.. Fuktioe
Hochschule Fchbereich Wirtschft Rheibch Bo-Rhei-Sieg Dipl.th.A.Füllebch Uiversity of Applied Scieces Vorlesug Wirtschftsmthemtik Studiegg Busiess Admiistrtio ud Wirtschftspsychologie . Alysis.. Fuktioe
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Formen der Arbeit mit mathematisch begabten Schülern in Russland 1
 Boris Averboukh Forme der Arbeit mit mthemtisch begbte Schüler i Russld Eie Ursche der mthemtische ud techische Erfolge i Russld des 0. Jhrhuderts wr die ktive Arbeit mit mthemtisch begbte Kider, der viele
Boris Averboukh Forme der Arbeit mit mthemtisch begbte Schüler i Russld Eie Ursche der mthemtische ud techische Erfolge i Russld des 0. Jhrhuderts wr die ktive Arbeit mit mthemtisch begbte Kider, der viele
Mathematik Vorkurs. Fachhochschule Konstanz Fachbereich Elektrotechnik & Informationstechnik Prof. Birkhölzer
 Mthemtik Vorkurs Fchhochschule Kostz Fchbereich Versio 5.8 Copright 0 Versio 5.8 Copright 0 Mthemtik Wozu, Wie, Ws?.... Mthemtik Wozu?..... Hitergrud: Aspekte der Mthemtik..... Mthemtische Aspekte im Alltg
Mthemtik Vorkurs Fchhochschule Kostz Fchbereich Versio 5.8 Copright 0 Versio 5.8 Copright 0 Mthemtik Wozu, Wie, Ws?.... Mthemtik Wozu?..... Hitergrud: Aspekte der Mthemtik..... Mthemtische Aspekte im Alltg
Kapitel 6 E-Mails schreiben und organisieren
 Kpitel 6 E-Mils shreien und orgnisieren Die Kommuniktion vi E-Mil ist heute essenziell. Und Ihr M ist estens gerüstet für den Empfng, ds Verfssen und die Orgnistion von E-Mils. Wie Sie effektiv mit dem
Kpitel 6 E-Mils shreien und orgnisieren Die Kommuniktion vi E-Mil ist heute essenziell. Und Ihr M ist estens gerüstet für den Empfng, ds Verfssen und die Orgnistion von E-Mils. Wie Sie effektiv mit dem
1 Analysis T1 Übungsblatt 1
 Aalysis T Übugsblatt A eier Weggabelug i der Wüste lebe zwei Brüder, die vollkomme gleich aussehe, zwische dee es aber eie gewaltige Uterschied gibt: Der eie sagt immer die Wahrheit, der adere lügt immer.
Aalysis T Übugsblatt A eier Weggabelug i der Wüste lebe zwei Brüder, die vollkomme gleich aussehe, zwische dee es aber eie gewaltige Uterschied gibt: Der eie sagt immer die Wahrheit, der adere lügt immer.
Differenziation 5 Ableitung der elementaren Funktionen 6 Differenziationsregeln 6 Ableitung der Umkehrfunktion
 Prof. Dr. Elmr Müller-Horsche FH Augsurg Formelsmmlug Igeieurmthemtik Ihlt (. Semester) Seite Grudegriffe 3 Trigoometrische Fuktioe 3 Additiostheoreme 3 Hl- Doppelwikelformel 3 Verschieuge ud Dehuge 4
Prof. Dr. Elmr Müller-Horsche FH Augsurg Formelsmmlug Igeieurmthemtik Ihlt (. Semester) Seite Grudegriffe 3 Trigoometrische Fuktioe 3 Additiostheoreme 3 Hl- Doppelwikelformel 3 Verschieuge ud Dehuge 4
Abschlussprüfung 2013 an den Realschulen in Bayern
 Prüfugsdauer: 50 Miute Abschlussprüfug 03 a de Realschule i Bayer Mathematik II Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Die ebestehede kizze zeigt de Axialschitt eier massive
Prüfugsdauer: 50 Miute Abschlussprüfug 03 a de Realschule i Bayer Mathematik II Name: Vorame: Klasse: Platzziffer: Pukte: Aufgabe A Haupttermi A 0 Die ebestehede kizze zeigt de Axialschitt eier massive
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Grundlagen der Technischen Informatik. Bausteine der Digitaltechnik - Binäre Schalter und Gatter. Kapitel 7.1
 Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Nachklausur - Analysis 1 - Lösungen
 Prof. Dr. László Székelyhidi Aalysis I, WS 212 Nachklausur - Aalysis 1 - Lösuge Aufgabe 1 (Folge ud Grezwerte). (i) (1 Pukt) Gebe Sie die Defiitio des Häufugspuktes eier reelle Zahlefolge (a ) N. Lösug:
Prof. Dr. László Székelyhidi Aalysis I, WS 212 Nachklausur - Aalysis 1 - Lösuge Aufgabe 1 (Folge ud Grezwerte). (i) (1 Pukt) Gebe Sie die Defiitio des Häufugspuktes eier reelle Zahlefolge (a ) N. Lösug:
MATHEMATIK F 1 MEG Sek II > Formeln. Formelsammlung. Mathematik. Sekundarstufe II. --- Grundlagen & Analysis ---
 MATHEMATIK F 1 MEG Sek II > Formel Formelsmmlug Mthemtik Sekudrstufe II --- Grudlge & Alysis --- MATHEMATIK F 2 MEG Sek II > Formel Ihltsverzeichis Zhlereiche & Itervlle...3 Termumformuge...3 Bruchrechug...3
MATHEMATIK F 1 MEG Sek II > Formel Formelsmmlug Mthemtik Sekudrstufe II --- Grudlge & Alysis --- MATHEMATIK F 2 MEG Sek II > Formel Ihltsverzeichis Zhlereiche & Itervlle...3 Termumformuge...3 Bruchrechug...3
LV "Grundlagen der Informatik" Programmierung in C (Teil 2)
 Aufgabekomplex: Programmiere i C (Teil vo ) (Strukturierte Datetype: Felder, Strukture, Zeiger; Fuktioe mit Parameterübergabe; Dateiarbeit) Hiweis: Alle mit * gekezeichete Aufgabe sid zum zusätzliche Übe
Aufgabekomplex: Programmiere i C (Teil vo ) (Strukturierte Datetype: Felder, Strukture, Zeiger; Fuktioe mit Parameterübergabe; Dateiarbeit) Hiweis: Alle mit * gekezeichete Aufgabe sid zum zusätzliche Übe
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Korrekturrichtlinie zur Studienleistung Wirtschaftsmathematik am 22.12.2007 Betriebswirtschaft BB-WMT-S11-071222
 Korrekturrichtliie zur Studieleistug Wirtschaftsmathematik am..007 Betriebswirtschaft BB-WMT-S-07 Für die Bewertug ud Abgabe der Studieleistug sid folgede Hiweise verbidlich: Die Vergabe der Pukte ehme
Korrekturrichtliie zur Studieleistug Wirtschaftsmathematik am..007 Betriebswirtschaft BB-WMT-S-07 Für die Bewertug ud Abgabe der Studieleistug sid folgede Hiweise verbidlich: Die Vergabe der Pukte ehme
Informatik II Dynamische Programmierung
 lausthal Iformatik II Dyamische Programmierug. Zachma lausthal Uiversity, ermay zach@i.tu-clausthal.de Zweite Techik für de Algorithmeetwurf Zum Name: "Dyamische " hat ichts mit "Dyamik" zu tu, soder mit
lausthal Iformatik II Dyamische Programmierug. Zachma lausthal Uiversity, ermay zach@i.tu-clausthal.de Zweite Techik für de Algorithmeetwurf Zum Name: "Dyamische " hat ichts mit "Dyamik" zu tu, soder mit
Zahlenfolgen, Grenzwerte und Zahlenreihen
 KAPITEL 5 Zahlefolge, Grezwerte ud Zahlereihe. Folge Defiitio 5.. Uter eier Folge reeller Zahle (oder eier reelle Zahlefolge) versteht ma eie auf N 0 erlarte reellwertige Futio, die jedem N 0 ei a R zuordet:
KAPITEL 5 Zahlefolge, Grezwerte ud Zahlereihe. Folge Defiitio 5.. Uter eier Folge reeller Zahle (oder eier reelle Zahlefolge) versteht ma eie auf N 0 erlarte reellwertige Futio, die jedem N 0 ei a R zuordet:
Wirtschaftsingenieurwesen Wirtschaftsmathematik Prüfungsleistung WI-WMT-P12 040703. Studiengang Fach Art der Leistung Klausur-Knz. Datum 03.07.
 Studiegag Fach Art der Leistug Klausur-Kz. Wirtschaftsigeieurwese Wirtschaftsmathematik Prüfugsleistug WI-WMT-P 040703 Datum 03.07.004 Bezüglich der Afertigug Ihrer Arbeit sid folgede Hiweise verbidlich:
Studiegag Fach Art der Leistug Klausur-Kz. Wirtschaftsigeieurwese Wirtschaftsmathematik Prüfugsleistug WI-WMT-P 040703 Datum 03.07.004 Bezüglich der Afertigug Ihrer Arbeit sid folgede Hiweise verbidlich:
Übungen zur Vorlesung Funktionentheorie Sommersemester 2012. Musterlösung zu Blatt 0
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Prof. Dr. Rolad Speicher M.Sc. Tobias Mai Übuge zur Vorlesug Fuktioetheorie Sommersemester 01 Musterlösug zu Blatt 0 Aufgabe 1. Käpt Schwarzbart,
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Prof. Dr. Rolad Speicher M.Sc. Tobias Mai Übuge zur Vorlesug Fuktioetheorie Sommersemester 01 Musterlösug zu Blatt 0 Aufgabe 1. Käpt Schwarzbart,
2. Diophantische Gleichungen
 2. Diophatische Gleichuge [Teschl05, S. 91f] 2.1. Was ist eie diophatische Gleichug ud wozu braucht ma sie? Def D2-1: Eie diophatische Gleichug ist eie Polyomfuktio i x,y,z,, bei der als Lösuge ur gaze
2. Diophatische Gleichuge [Teschl05, S. 91f] 2.1. Was ist eie diophatische Gleichug ud wozu braucht ma sie? Def D2-1: Eie diophatische Gleichug ist eie Polyomfuktio i x,y,z,, bei der als Lösuge ur gaze
Lernhilfe in Form eines ebooks
 Ziseszisrechug Lerhilfe i Form eies ebooks apitel Thema Seite 1 Vorwort ud Eiführug 2 2 Theorie der Ziseszisrechug 5 3 Beispiele ud Beispielrechuge 12 4 Testaufgabe mit Lösuge 18 Zis-Ziseszis.de 212 Seite
Ziseszisrechug Lerhilfe i Form eies ebooks apitel Thema Seite 1 Vorwort ud Eiführug 2 2 Theorie der Ziseszisrechug 5 3 Beispiele ud Beispielrechuge 12 4 Testaufgabe mit Lösuge 18 Zis-Ziseszis.de 212 Seite
Kapitel 4: Stationäre Prozesse
 Kapitel 4: Statioäre Prozesse M. Scheutzow Jauary 6, 2010 4.1 Maßerhaltede Trasformatioe I diesem Kapitel führe wir zuächst de Begriff der maßerhaltede Trasformatio auf eiem Wahrscheilichkeitsraum ei ud
Kapitel 4: Statioäre Prozesse M. Scheutzow Jauary 6, 2010 4.1 Maßerhaltede Trasformatioe I diesem Kapitel führe wir zuächst de Begriff der maßerhaltede Trasformatio auf eiem Wahrscheilichkeitsraum ei ud
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
2. Einführung in die Geometrische Optik
 2. Eiührug i die Geometrische Optik 2. Allgemeie Prizipie 2.. Licht ud Materie Optische Ssteme werde ür de Spektralbereich zwische dem extreme Ultraviolette ( m) ud dem thermische Irarote (Q-Bad bei 2
2. Eiührug i die Geometrische Optik 2. Allgemeie Prizipie 2.. Licht ud Materie Optische Ssteme werde ür de Spektralbereich zwische dem extreme Ultraviolette ( m) ud dem thermische Irarote (Q-Bad bei 2
Aufgaben zur vollständigen Induktion
 c 7 by Raier Müller - Aufgabe zur vollstädige Idutio We ichts aderes agegebe ist, da gelte die Behauptuge für IN {; ; ;...}. A) Teilbareit: ) ist gerade (d.h. durch teilbar). ) ist durch teilbar. ) ist
c 7 by Raier Müller - Aufgabe zur vollstädige Idutio We ichts aderes agegebe ist, da gelte die Behauptuge für IN {; ; ;...}. A) Teilbareit: ) ist gerade (d.h. durch teilbar). ) ist durch teilbar. ) ist
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Wirtschaftsmathematik
 Studiegag Betriebswirtschaft Fach Wirtschaftsmathematik Art der Leistug Studieleistug Klausur-Kz. BW-WMT-S1 040508 Datum 08.05.004 Bezüglich der Afertigug Ihrer Arbeit sid folgede Hiweise verbidlich: Verwede
Studiegag Betriebswirtschaft Fach Wirtschaftsmathematik Art der Leistug Studieleistug Klausur-Kz. BW-WMT-S1 040508 Datum 08.05.004 Bezüglich der Afertigug Ihrer Arbeit sid folgede Hiweise verbidlich: Verwede
Allgemeine Lösungen der n-dimensionalen Laplace-Gleichung und ihre komplexe Variable
 Allgemeie Lösuge der -dimesioale Laplace-Gleichug ud ihre komplexe Variable Dr. rer. at. Kuag-lai Chao Göttige, de 4. Jauar 01 Abstract Geeral solutios of the -dimesioal Laplace equatio ad its complex
Allgemeie Lösuge der -dimesioale Laplace-Gleichug ud ihre komplexe Variable Dr. rer. at. Kuag-lai Chao Göttige, de 4. Jauar 01 Abstract Geeral solutios of the -dimesioal Laplace equatio ad its complex
ADSORPTIONS-ISOTHERME
 Institut für Physiklishe Chemie Prktikum Teil und B 8. DSORPTIONS-ISOTHERME Stnd 30/0/008 DSORPTIONS-ISOTHERME. Versuhspltz Komponenten: - Büretten - Pipetten - Shütteltish - Wge - Filtriergestell - Behergläser.
Institut für Physiklishe Chemie Prktikum Teil und B 8. DSORPTIONS-ISOTHERME Stnd 30/0/008 DSORPTIONS-ISOTHERME. Versuhspltz Komponenten: - Büretten - Pipetten - Shütteltish - Wge - Filtriergestell - Behergläser.
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
Hilfsrelais HR 116. Bilfinger Mauell GmbH
 Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Satz Ein Boolescher Term t ist eine Tautologie genau dann, wenn t unerfüllbar ist.
 Erfüllbarkeit, Uerfüllbarkeit, Allgemeigültigkeit Defiitio Eie Belegug β ist passed zu eiem Boolesche Term t, falls β für alle atomare Terme i t defiiert ist. (Wird ab jetzt ageomme.) Ist β(t) = true,
Erfüllbarkeit, Uerfüllbarkeit, Allgemeigültigkeit Defiitio Eie Belegug β ist passed zu eiem Boolesche Term t, falls β für alle atomare Terme i t defiiert ist. (Wird ab jetzt ageomme.) Ist β(t) = true,
2 Kinobesuch GRAMMATIK. perfekt. Im September LEICHT. wann die Vorstellung beginnt. Schreiben Sie Sätze! Beginnen Sie mit den grün markierten Wörtern!
 DEUTSCH GRAMMATIK VERBPOSITION S. 0 Im Septemer LEICHT Shreien Sie Sätze! Beginnen Sie mit den grün mrkierten Wörtern! der Herst / m. Septemer / eginnt ds Oktoerfest / in Münhen / findet sttt die Österreiher
DEUTSCH GRAMMATIK VERBPOSITION S. 0 Im Septemer LEICHT Shreien Sie Sätze! Beginnen Sie mit den grün mrkierten Wörtern! der Herst / m. Septemer / eginnt ds Oktoerfest / in Münhen / findet sttt die Österreiher
Bitte schicken Sie mir eine E-mail, wenn Sie einen Fehler gefunden haben 1. Moritz Kaßmann
 Das folgede Skript zur Vorlesug Spezielle Aspekte der Aalysis für Studierede des Lehramts a Grud, Haupt ud Realschule wird fortlaufed aktualisiert ud verädert werde. Das Skript ethält bei weitem icht alle
Das folgede Skript zur Vorlesug Spezielle Aspekte der Aalysis für Studierede des Lehramts a Grud, Haupt ud Realschule wird fortlaufed aktualisiert ud verädert werde. Das Skript ethält bei weitem icht alle
Übungsblatt 1 zur Vorlesung Angewandte Stochastik
 Dr Christoph Luchsiger Übugsblatt 1 zur Vorlesug Agewadte Stochastik Repetitio WT Herausgabe des Übugsblattes: Woche 9, Abgabe der Lösuge: Woche 1 (bis Freitag, 1615 Uhr), Rückgabe ud Besprechug: Woche
Dr Christoph Luchsiger Übugsblatt 1 zur Vorlesug Agewadte Stochastik Repetitio WT Herausgabe des Übugsblattes: Woche 9, Abgabe der Lösuge: Woche 1 (bis Freitag, 1615 Uhr), Rückgabe ud Besprechug: Woche
BINOMIALKOEFFIZIENTEN. Stochastik und ihre Didaktik Referentin: Iris Winkler 10.11.2008
 Stochasti ud ihre Didati Refereti: Iris Wiler 10.11.2008 Aufgabe: Führe Sie i der Seudarstufe II die Biomialoeffiziete als ombiatorisches Azahlproblem ei. Erarbeite Sie mit de Schülerie ud Schüler mithilfe
Stochasti ud ihre Didati Refereti: Iris Wiler 10.11.2008 Aufgabe: Führe Sie i der Seudarstufe II die Biomialoeffiziete als ombiatorisches Azahlproblem ei. Erarbeite Sie mit de Schülerie ud Schüler mithilfe
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
Stochastik für WiWi - Klausurvorbereitung
 Dr. Markus Kuze WS 2013/14 Dipl.-Math. Stefa Roth 11.02.2014 Stochastik für WiWi - Klausurvorbereitug Gesetz der totale Wahrscheilichkeit ud Satz vo Bayes (Ω, F, P) Wahrscheilichkeitsraum, E 1,..., E F
Dr. Markus Kuze WS 2013/14 Dipl.-Math. Stefa Roth 11.02.2014 Stochastik für WiWi - Klausurvorbereitug Gesetz der totale Wahrscheilichkeit ud Satz vo Bayes (Ω, F, P) Wahrscheilichkeitsraum, E 1,..., E F
Betriebswirtschaft Wirtschaftsmathematik Studienleistung BW-WMT-S12 011110
 Name, Vorame Matrikel-Nr. Studiezetrum Studiegag Fach Art der Leistug Klausur-Kz. Betriebswirtschaft Wirtschaftsmathematik Studieleistug Datum 10.11.2001 BW-WMT-S12 011110 Verwede Sie ausschließlich das
Name, Vorame Matrikel-Nr. Studiezetrum Studiegag Fach Art der Leistug Klausur-Kz. Betriebswirtschaft Wirtschaftsmathematik Studieleistug Datum 10.11.2001 BW-WMT-S12 011110 Verwede Sie ausschließlich das
Physikalische Grundlagen: Strahlengang durch optische Systeme
 ieser Text ist ür iteressierte Leser gedacht, die sich über die klausur-relevate, physiologische Grudlage hiaus mit der Optik des Auges beschätige wolle! Physikalische Grudlage: Strahlegag durch optische
ieser Text ist ür iteressierte Leser gedacht, die sich über die klausur-relevate, physiologische Grudlage hiaus mit der Optik des Auges beschätige wolle! Physikalische Grudlage: Strahlegag durch optische
Identifizierbarkeit von Sprachen
 FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
FRIEDRICH SCHILLER UNIVERSITÄT JENA Fkultät für Mthemtik und Informtik INSTITUT für INFORMATIK VORLESUNG IM WINTERSEMESTER STOCHASTISCHE GRAMMATIKMODELLE Ernst Günter Schukt-Tlmzzini 06. Quelle: /home/schukt/ltex/folien/sprchmodelle-00/ssm-06.tex
15.4 Diskrete Zufallsvariablen
 .4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
.4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
Wahrscheinlichkeit & Statistik
 Wahrscheilichkeit & Statistik created by Versio: 3. Jui 005 www.matheachhilfe.ch ifo@matheachhilfe.ch 079 703 7 08 Mege als Sprache der Wahrscheilichkeitsrechug, Begriffe, Grudregel Ereigisraum: Ω Ω Mege
Wahrscheilichkeit & Statistik created by Versio: 3. Jui 005 www.matheachhilfe.ch ifo@matheachhilfe.ch 079 703 7 08 Mege als Sprache der Wahrscheilichkeitsrechug, Begriffe, Grudregel Ereigisraum: Ω Ω Mege
1 = 1. 6 Induktionsannahme: Die Formal gelte für n = k. Induktionsschritt: Gültigkeit der Formel für k+1: 1 2 + 2 2 +... + k 2 + (k + 1) 2 = 2 = 6 = 6
 65 Eric Müller Vollstädige Iduktio Nach GIUSEPPE PEANO (858-93) ka ma die Mege N der atürliche Zahle durch folgede Axiome defiiere []:. ist eie atürliche Zahl.. Zu jeder atürliche Zahl gibt es geau eie
65 Eric Müller Vollstädige Iduktio Nach GIUSEPPE PEANO (858-93) ka ma die Mege N der atürliche Zahle durch folgede Axiome defiiere []:. ist eie atürliche Zahl.. Zu jeder atürliche Zahl gibt es geau eie
Sie das Gerät aus und überprüfen Sie den Lieferumfang. Netzkabel. Trägerbogen/Plastikkarten-Trägerbogen DVD-ROM
 Instlltionsnleitung Hier eginnen ADS-2100 Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät einrihten. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Instlltionsnleitung Hier eginnen ADS-2100 Lesen Sie zuerst die Produkt-Siherheitshinweise, evor Sie ds Gerät einrihten. Lesen Sie dnn diese Instlltionsnleitung zur korrekten Einrihtung und Instlltion.
Seminar zum anorganisch-chemischen Praktikum. Quantitative Analyse. Patrick Schwarz
 Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Tao De / Pan JiaWei. Ihrig/Pflaumer Finanzmathematik Oldenburg Verlag 1999 =7.173,55 DM. ges: A m, A v
 Tao De / Pa JiaWei Ihrig/Pflaumer Fiazmathematik Oldeburg Verlag 1999 1..Ei Darlehe vo. DM soll moatlich mit 1% verzist ud i Jahre durch kostate Auitäte getilgt werde. Wie hoch sid a) die Moatsrate? b)
Tao De / Pa JiaWei Ihrig/Pflaumer Fiazmathematik Oldeburg Verlag 1999 1..Ei Darlehe vo. DM soll moatlich mit 1% verzist ud i Jahre durch kostate Auitäte getilgt werde. Wie hoch sid a) die Moatsrate? b)
3. Tilgungsrechnung. 3.1. Tilgungsarten
 schreier@math.tu-freiberg.de 03731) 39 2261 3. Tilgugsrechug Die Tilgugsrechug beschäftigt sich mit der Rückzahlug vo Kredite, Darlehe ud Hypotheke. Dabei erwartet der Gläubiger, daß der Schulder seie
schreier@math.tu-freiberg.de 03731) 39 2261 3. Tilgugsrechug Die Tilgugsrechug beschäftigt sich mit der Rückzahlug vo Kredite, Darlehe ud Hypotheke. Dabei erwartet der Gläubiger, daß der Schulder seie
Die nächste Übung ist vom 12.1. auf den 19.1.2012 verlegt worden.
 Allgemeines Einige Hinweise: Die nähste Üung ist vom.. auf den 9..0 verlegt worden. Die alten Klausuren findet Ihr unter folgendem Link: http://www.wiwi.uni muenster.de/vwt/studieren/pruefungen_marktpreis.htm
Allgemeines Einige Hinweise: Die nähste Üung ist vom.. auf den 9..0 verlegt worden. Die alten Klausuren findet Ihr unter folgendem Link: http://www.wiwi.uni muenster.de/vwt/studieren/pruefungen_marktpreis.htm
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Istitut für tochastik Prof. Dr. N. Bäuerle Dipl.-Math.. Urba Lösugsvorschlag 9. Übugsblatt zur Vorlesug Fiazmathematik I Aufgabe Ei euartiges Derivat) Wir sid i eiem edliche, arbitragefreie Fiazmarkt,
Istitut für tochastik Prof. Dr. N. Bäuerle Dipl.-Math.. Urba Lösugsvorschlag 9. Übugsblatt zur Vorlesug Fiazmathematik I Aufgabe Ei euartiges Derivat) Wir sid i eiem edliche, arbitragefreie Fiazmarkt,
GIBS. Übungsaufgaben zur Vertiefung. V1. Beschriften Sie die Konstruktionen! n n n n ' ' ' ' Modul 1.5. Geometrische Optik 1 58.
 eometrische Optik 1 58 Übugsaufgabe zur Vertiefug V1. Beschrifte Sie die Kostruktioe! ' ' ' ' ' ' ' ' Lehrerversio eometrische Optik 1 59 V2. Bei eiem Brillekroglas tritt Licht a der Rückfläche des lases
eometrische Optik 1 58 Übugsaufgabe zur Vertiefug V1. Beschrifte Sie die Kostruktioe! ' ' ' ' ' ' ' ' Lehrerversio eometrische Optik 1 59 V2. Bei eiem Brillekroglas tritt Licht a der Rückfläche des lases
Zusammenfassung Wirtschaftsinformatik Stefan Käßmann
 I. Iformatio ud Nachricht 1. Iformatio ud Nachricht - Nachricht (Sytax), Sigale, Zeiche - Iformatio (Sematik), bit - Rausche 2. digitale Nachrichte - digitale Sigale (Sigalparameter aus edlicher Zeichevorrat)
I. Iformatio ud Nachricht 1. Iformatio ud Nachricht - Nachricht (Sytax), Sigale, Zeiche - Iformatio (Sematik), bit - Rausche 2. digitale Nachrichte - digitale Sigale (Sigalparameter aus edlicher Zeichevorrat)
Wintersemester 2006/2007, Universität Rostock Abgabetermin: spätestens 24.10.2006, 09:00 Uhr. Aufgabe 1.1: (5 P)
 Serie Abgabetermi: spätestes 24.0.2006, 09:00 Uhr Aufgabe.: 5 P Zeige Sie, dass das geometrische Mittel icht größer ist als das arithmetische Mittel, d.h., dass für alle Zahle a, b R mit a, b 0 gilt ab
Serie Abgabetermi: spätestes 24.0.2006, 09:00 Uhr Aufgabe.: 5 P Zeige Sie, dass das geometrische Mittel icht größer ist als das arithmetische Mittel, d.h., dass für alle Zahle a, b R mit a, b 0 gilt ab
IWW Studienprogramm. Aufbaustudium. Gründungscontrolling. Lösungshinweise zur 3. Musterklausur
 Istitut für Wirtschaftswisseschaftliche Forschug ud Weiterbildug GmbH Istitut a der FerUiversität i Hage IWW Studieprogramm Aufbaustudium Grüdugscotrollig Lösugshiweise zur 3. Musterklausur Lösugshiweise
Istitut für Wirtschaftswisseschaftliche Forschug ud Weiterbildug GmbH Istitut a der FerUiversität i Hage IWW Studieprogramm Aufbaustudium Grüdugscotrollig Lösugshiweise zur 3. Musterklausur Lösugshiweise
Controlling als strategisches Mittel im Multiprojektmanagement von Rudolf Fiedler
 von udolf Fiedler Zusmmenfssung: Der Beitrg eshreit die Aufgen des Projektontrollings, insesondere des strtegishen Projektontrollings. Für die wesentlihen Aufgenereihe werden prktikle Instrumente vorgestellt.
von udolf Fiedler Zusmmenfssung: Der Beitrg eshreit die Aufgen des Projektontrollings, insesondere des strtegishen Projektontrollings. Für die wesentlihen Aufgenereihe werden prktikle Instrumente vorgestellt.
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
